Рассмотрим простейшие модели производства и потребления. Модели производства строятся с помощью производственных функций, а модели потребления на основе целевой функции потребления.
Производственные функции и их характеристики
Простейшую модель производства можно представить как некоторую систему, перерабатывающую различные виды ресурсов в готовую продукцию.  В качестве ресурсов могут выступать:
1. сырье;
2. трудовые затраты;
3. энергозатраты;
4. научно-исследовательские ресурсы;
5. технологические ресурсы;
6. транспортные ресурсы и др.
Производственной функцией называется зависимость между объёмом произведённой продукции у, и затратами различных видов ресурсов, необходимых для выпуска этой продукции В качестве ресурсов могут выступать:
1. сырье;
2. трудовые затраты;
3. энергозатраты;
4. научно-исследовательские ресурсы;
5. технологические ресурсы;
6. транспортные ресурсы и др.
Производственной функцией называется зависимость между объёмом произведённой продукции у, и затратами различных видов ресурсов, необходимых для выпуска этой продукции  : :  . На практике для упрощения модели часто используют двухфакторную производственную функцию . На практике для упрощения модели часто используют двухфакторную производственную функцию 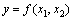 , включающую два вида ресурсов: 1. материальные , включающую два вида ресурсов: 1. материальные 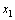 , включающие затраты сырья, энергии, транспортные и др. ресурсы; 2. трудовые ресурсы , включающие затраты сырья, энергии, транспортные и др. ресурсы; 2. трудовые ресурсы  . Производственная функция должна удовлетворять ряду требований: 1. Без затрат ресурсов нет выпуска: f (0,0)=0. 2. С увеличением затрат любого из ресурсов выпуск растёт, т.е. производственная функция должна быть возрастающей по любому из факторов. . Производственная функция должна удовлетворять ряду требований: 1. Без затрат ресурсов нет выпуска: f (0,0)=0. 2. С увеличением затрат любого из ресурсов выпуск растёт, т.е. производственная функция должна быть возрастающей по любому из факторов.  3. Закон убывания эффективности: при одних и тех же абсолютных увеличениях затрат любого из ресурсов Δ х прирост объёма производства Δ у тем меньше, чем больше выпуск продукции. Другими словами, производственная функция должна быть выпуклой по каждому аргументу. Зная производственную функцию, можно рассчитать ряд числовых характеристик. Рассмотрим основные из них. 1. Средней производительностью по каждому ресурсу называются величины: 3. Закон убывания эффективности: при одних и тех же абсолютных увеличениях затрат любого из ресурсов Δ х прирост объёма производства Δ у тем меньше, чем больше выпуск продукции. Другими словами, производственная функция должна быть выпуклой по каждому аргументу. Зная производственную функцию, можно рассчитать ряд числовых характеристик. Рассмотрим основные из них. 1. Средней производительностью по каждому ресурсу называются величины:  , ,  , которые имеют смысл среднего выпуска продукции из расчета единичных затрат данного ресурса. Если , которые имеют смысл среднего выпуска продукции из расчета единичных затрат данного ресурса. Если 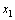 - материальные затраты, а - материальные затраты, а  - трудовые, то A 1 называется капиталоотдачей, а А 2 - называется производительностью труда. 2. Предельной или маржинальной производительностью по каждому ресурсу называются величины: - трудовые, то A 1 называется капиталоотдачей, а А 2 - называется производительностью труда. 2. Предельной или маржинальной производительностью по каждому ресурсу называются величины:  , ,  . Эти величины показывают приближённо на сколько единиц изменится выпуск, если затраты того или иного ресурса изменятся на единицу: . Эти величины показывают приближённо на сколько единиц изменится выпуск, если затраты того или иного ресурса изменятся на единицу: 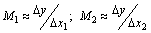 . 3. Частной эластичностью по каждому ресурсу называются величины: . 3. Частной эластичностью по каждому ресурсу называются величины:  Эластичности приближенно показывают на сколько процентов изменится выпуск, если затраты того или иного ресурса изменятся на один процент: Эластичности приближенно показывают на сколько процентов изменится выпуск, если затраты того или иного ресурса изменятся на один процент: 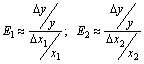 . Величина . Величина  называется полной эластичностью или эластичностью производства. 4. Технологической нормой замены называется величина называется полной эластичностью или эластичностью производства. 4. Технологической нормой замены называется величина  , которая приближенно показывает как изменится выпуск, если единицу одного ресурса заменить единицей другого. ПРИМЕР. Производственная функция имеет вид , которая приближенно показывает как изменится выпуск, если единицу одного ресурса заменить единицей другого. ПРИМЕР. Производственная функция имеет вид  . Найти средние и предельные производительности, эластичности, технологическую норму замены. Решение. Средние производительности равны: . Найти средние и предельные производительности, эластичности, технологическую норму замены. Решение. Средние производительности равны: 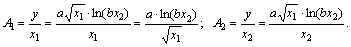 Предельные производительности равны: Предельные производительности равны:  Эластичности равны: Эластичности равны:  Технологическая норма замены есть Технологическая норма замены есть 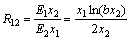 .
Линейная и Кобба-Дугласа производственные функции
На практике при моделировании реальных производств чаще всего используют два вида производственных функций: линейная и Кобба-Дугласа. Линейная производственная функция имеет вид: .
Линейная и Кобба-Дугласа производственные функции
На практике при моделировании реальных производств чаще всего используют два вида производственных функций: линейная и Кобба-Дугласа. Линейная производственная функция имеет вид:  . Она строится в случаях, когда объем выпуска пропорционален затратам. Однако данная функция не удовлетворяет . Она строится в случаях, когда объем выпуска пропорционален затратам. Однако данная функция не удовлетворяет  первому и третьему требованиям к производственным функциям, поэтому ее можно использовать для приближения реальных функций на небольших локальных участках изменения их аргументов (см. рисунок). Для выполнения второго требования необходимо выполнение условий первому и третьему требованиям к производственным функциям, поэтому ее можно использовать для приближения реальных функций на небольших локальных участках изменения их аргументов (см. рисунок). Для выполнения второго требования необходимо выполнение условий 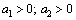 . Производственная функция Кобба-Дугласа имеет вид: . Производственная функция Кобба-Дугласа имеет вид:  . Для выполнения всех требований к производственным функциям необходимо выполнение условий: . Для выполнения всех требований к производственным функциям необходимо выполнение условий:  Найдем средние и предельные производительности, эластичности, технологическую норму замены для линейной и Кобба-Дугласа производственных функций. Для линейной функции Найдем средние и предельные производительности, эластичности, технологическую норму замены для линейной и Кобба-Дугласа производственных функций. Для линейной функции  будет: будет:   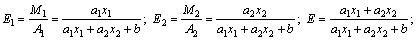  Таким образом, коэффициенты а 1 и а 2 линейной производственной функции имеют смысл предельных производительностей и их можно вычислять по формулам: Таким образом, коэффициенты а 1 и а 2 линейной производственной функции имеют смысл предельных производительностей и их можно вычислять по формулам: 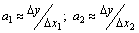 . (6.1) Для производственной функции Кобба-Дугласа . (6.1) Для производственной функции Кобба-Дугласа  будет: будет:   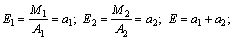  Таким образом, коэффициенты а 1 и а 2 производственной функции Кобба-Дугласа имеют смысл частных эластичностей и их можно вычислять по формулам: Таким образом, коэффициенты а 1 и а 2 производственной функции Кобба-Дугласа имеют смысл частных эластичностей и их можно вычислять по формулам: 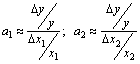 (6.2) Пример. Некоторое предприятие, затрачивая для производства 65 единиц материальных затрат и 17 трудовых, выпускало 120 единиц продукции. В результате расширения и увеличении материальных затрат до 68 единиц выпуск возрос до 124 единиц, а при увеличении трудозатрат до 19 единиц выпуск вырос до 127 единиц. Составить линейную производственную функцию и функцию Кобба-Дугласа. Решение. (6.2) Пример. Некоторое предприятие, затрачивая для производства 65 единиц материальных затрат и 17 трудовых, выпускало 120 единиц продукции. В результате расширения и увеличении материальных затрат до 68 единиц выпуск возрос до 124 единиц, а при увеличении трудозатрат до 19 единиц выпуск вырос до 127 единиц. Составить линейную производственную функцию и функцию Кобба-Дугласа. Решение.
| Записав для удобства исходные данные в виде таблицы и применив формулы (8.1) и (8.2), рассчитываем параметры производственных функций.
| |
Линейная функция  . Для нахождения параметров а 1 и а 2 используем формулу (8.1): . Для нахождения параметров а 1 и а 2 используем формулу (8.1):

Получаем  . Для нахождения b подставляем в уравнение исходные данные из 2-го столбца таблицы: . Для нахождения b подставляем в уравнение исходные данные из 2-го столбца таблицы: 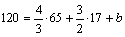 решаем уравнение относительно b, получаем решаем уравнение относительно b, получаем 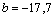 . В итоге получаем линейную производственную функцию . В итоге получаем линейную производственную функцию 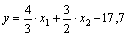 . .
Производственная функция Кобба-Дугласа имеет вид  . По формуле (8.2) находим коэффициенты уравнения: . По формуле (8.2) находим коэффициенты уравнения:
 . .
Получаем уравнение вида 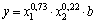 . Для нахождения b подставляем в уравнение исходные данные из 2-го столбца таблицы: . Для нахождения b подставляем в уравнение исходные данные из 2-го столбца таблицы: 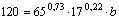 . Вычисляя, получаем . Вычисляя, получаем 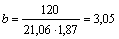 . В результате, производственная функция имеет вид: . В результате, производственная функция имеет вид: 
|

 В качестве ресурсов могут выступать:
1. сырье;
2. трудовые затраты;
3. энергозатраты;
4. научно-исследовательские ресурсы;
5. технологические ресурсы;
6. транспортные ресурсы и др.
Производственной функцией называется зависимость между объёмом произведённой продукции у, и затратами различных видов ресурсов, необходимых для выпуска этой продукции
В качестве ресурсов могут выступать:
1. сырье;
2. трудовые затраты;
3. энергозатраты;
4. научно-исследовательские ресурсы;
5. технологические ресурсы;
6. транспортные ресурсы и др.
Производственной функцией называется зависимость между объёмом произведённой продукции у, и затратами различных видов ресурсов, необходимых для выпуска этой продукции  :
:  . На практике для упрощения модели часто используют двухфакторную производственную функцию
. На практике для упрощения модели часто используют двухфакторную производственную функцию 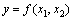 , включающую два вида ресурсов: 1. материальные
, включающую два вида ресурсов: 1. материальные 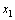 , включающие затраты сырья, энергии, транспортные и др. ресурсы; 2. трудовые ресурсы
, включающие затраты сырья, энергии, транспортные и др. ресурсы; 2. трудовые ресурсы  . Производственная функция должна удовлетворять ряду требований: 1. Без затрат ресурсов нет выпуска: f (0,0)=0. 2. С увеличением затрат любого из ресурсов выпуск растёт, т.е. производственная функция должна быть возрастающей по любому из факторов.
. Производственная функция должна удовлетворять ряду требований: 1. Без затрат ресурсов нет выпуска: f (0,0)=0. 2. С увеличением затрат любого из ресурсов выпуск растёт, т.е. производственная функция должна быть возрастающей по любому из факторов.  3. Закон убывания эффективности: при одних и тех же абсолютных увеличениях затрат любого из ресурсов Δ х прирост объёма производства Δ у тем меньше, чем больше выпуск продукции. Другими словами, производственная функция должна быть выпуклой по каждому аргументу. Зная производственную функцию, можно рассчитать ряд числовых характеристик. Рассмотрим основные из них. 1. Средней производительностью по каждому ресурсу называются величины:
3. Закон убывания эффективности: при одних и тех же абсолютных увеличениях затрат любого из ресурсов Δ х прирост объёма производства Δ у тем меньше, чем больше выпуск продукции. Другими словами, производственная функция должна быть выпуклой по каждому аргументу. Зная производственную функцию, можно рассчитать ряд числовых характеристик. Рассмотрим основные из них. 1. Средней производительностью по каждому ресурсу называются величины:  ,
,  , которые имеют смысл среднего выпуска продукции из расчета единичных затрат данного ресурса. Если
, которые имеют смысл среднего выпуска продукции из расчета единичных затрат данного ресурса. Если 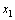 - материальные затраты, а
- материальные затраты, а  - трудовые, то A 1 называется капиталоотдачей, а А 2 - называется производительностью труда. 2. Предельной или маржинальной производительностью по каждому ресурсу называются величины:
- трудовые, то A 1 называется капиталоотдачей, а А 2 - называется производительностью труда. 2. Предельной или маржинальной производительностью по каждому ресурсу называются величины:  ,
,  . Эти величины показывают приближённо на сколько единиц изменится выпуск, если затраты того или иного ресурса изменятся на единицу:
. Эти величины показывают приближённо на сколько единиц изменится выпуск, если затраты того или иного ресурса изменятся на единицу: 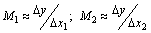 . 3. Частной эластичностью по каждому ресурсу называются величины:
. 3. Частной эластичностью по каждому ресурсу называются величины:  Эластичности приближенно показывают на сколько процентов изменится выпуск, если затраты того или иного ресурса изменятся на один процент:
Эластичности приближенно показывают на сколько процентов изменится выпуск, если затраты того или иного ресурса изменятся на один процент: 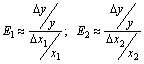 . Величина
. Величина  называется полной эластичностью или эластичностью производства. 4. Технологической нормой замены называется величина
называется полной эластичностью или эластичностью производства. 4. Технологической нормой замены называется величина  , которая приближенно показывает как изменится выпуск, если единицу одного ресурса заменить единицей другого. ПРИМЕР. Производственная функция имеет вид
, которая приближенно показывает как изменится выпуск, если единицу одного ресурса заменить единицей другого. ПРИМЕР. Производственная функция имеет вид  . Найти средние и предельные производительности, эластичности, технологическую норму замены. Решение. Средние производительности равны:
. Найти средние и предельные производительности, эластичности, технологическую норму замены. Решение. Средние производительности равны: 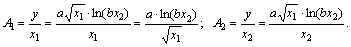 Предельные производительности равны:
Предельные производительности равны:  Эластичности равны:
Эластичности равны:  Технологическая норма замены есть
Технологическая норма замены есть 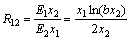 .
Линейная и Кобба-Дугласа производственные функции
На практике при моделировании реальных производств чаще всего используют два вида производственных функций: линейная и Кобба-Дугласа. Линейная производственная функция имеет вид:
.
Линейная и Кобба-Дугласа производственные функции
На практике при моделировании реальных производств чаще всего используют два вида производственных функций: линейная и Кобба-Дугласа. Линейная производственная функция имеет вид:  . Она строится в случаях, когда объем выпуска пропорционален затратам. Однако данная функция не удовлетворяет
. Она строится в случаях, когда объем выпуска пропорционален затратам. Однако данная функция не удовлетворяет  первому и третьему требованиям к производственным функциям, поэтому ее можно использовать для приближения реальных функций на небольших локальных участках изменения их аргументов (см. рисунок). Для выполнения второго требования необходимо выполнение условий
первому и третьему требованиям к производственным функциям, поэтому ее можно использовать для приближения реальных функций на небольших локальных участках изменения их аргументов (см. рисунок). Для выполнения второго требования необходимо выполнение условий 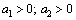 . Производственная функция Кобба-Дугласа имеет вид:
. Производственная функция Кобба-Дугласа имеет вид:  . Для выполнения всех требований к производственным функциям необходимо выполнение условий:
. Для выполнения всех требований к производственным функциям необходимо выполнение условий:  Найдем средние и предельные производительности, эластичности, технологическую норму замены для линейной и Кобба-Дугласа производственных функций. Для линейной функции
Найдем средние и предельные производительности, эластичности, технологическую норму замены для линейной и Кобба-Дугласа производственных функций. Для линейной функции  будет:
будет: 

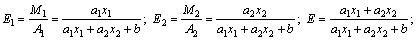
 Таким образом, коэффициенты а 1 и а 2 линейной производственной функции имеют смысл предельных производительностей и их можно вычислять по формулам:
Таким образом, коэффициенты а 1 и а 2 линейной производственной функции имеют смысл предельных производительностей и их можно вычислять по формулам: 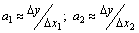 . (6.1) Для производственной функции Кобба-Дугласа
. (6.1) Для производственной функции Кобба-Дугласа  будет:
будет: 

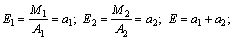
 Таким образом, коэффициенты а 1 и а 2 производственной функции Кобба-Дугласа имеют смысл частных эластичностей и их можно вычислять по формулам:
Таким образом, коэффициенты а 1 и а 2 производственной функции Кобба-Дугласа имеют смысл частных эластичностей и их можно вычислять по формулам: 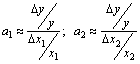 (6.2) Пример. Некоторое предприятие, затрачивая для производства 65 единиц материальных затрат и 17 трудовых, выпускало 120 единиц продукции. В результате расширения и увеличении материальных затрат до 68 единиц выпуск возрос до 124 единиц, а при увеличении трудозатрат до 19 единиц выпуск вырос до 127 единиц. Составить линейную производственную функцию и функцию Кобба-Дугласа. Решение.
(6.2) Пример. Некоторое предприятие, затрачивая для производства 65 единиц материальных затрат и 17 трудовых, выпускало 120 единиц продукции. В результате расширения и увеличении материальных затрат до 68 единиц выпуск возрос до 124 единиц, а при увеличении трудозатрат до 19 единиц выпуск вырос до 127 единиц. Составить линейную производственную функцию и функцию Кобба-Дугласа. Решение.

 . Для нахождения b подставляем в уравнение исходные данные из 2-го столбца таблицы:
. Для нахождения b подставляем в уравнение исходные данные из 2-го столбца таблицы: 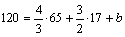 решаем уравнение относительно b, получаем
решаем уравнение относительно b, получаем 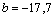 . В итоге получаем линейную производственную функцию
. В итоге получаем линейную производственную функцию 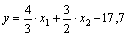 .
. .
.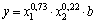 . Для нахождения b подставляем в уравнение исходные данные из 2-го столбца таблицы:
. Для нахождения b подставляем в уравнение исходные данные из 2-го столбца таблицы: 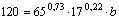 . Вычисляя, получаем
. Вычисляя, получаем 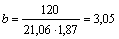 . В результате, производственная функция имеет вид:
. В результате, производственная функция имеет вид: 