Определение вероятности события, используя биномиальное распределение

Для данной выборки значений выходного параметра процесса, полученной дублированием эксперимента при неизменных значениях управляющих факторов, исключить выбросы, определить числовые характеристики выборки, построить доверительный интервал для математического ожидания.

Методика выполнения заданий контрольной работы

4.1.1. Определить наличие “выбросов” в представленной выборке и при наличии таковых исключить их из дальнейших расчетов.

Запишите все элементы выборки в порядке возрастания их значений. Определите величину критического значения для определения выброса по формуле 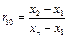, где: x ₁, x ₂, x _n – значения первого, второго и последнего элементов выборки, расположенных в порядке возрастания значений.

Сравните величину r ₁₀ с критическим значением (таблица 1). В случае, если r ₁₀ меньше критического значения - x ₁ не является выбросом, а если r ₁₀ больше критического значения - x ₁ является выбросом и его необходимо исключить из дальнейших расчетов.

Запишите все элементы выборки в порядке убывания их значений. Определите величину критического значения для определения выброса по формуле 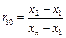, где: x ₁, x ₂, x _n – значения первого, второго и последнего элементов выборки, расположенных в порядке убывания значений.

Таблица 1

Критические значения для проверки выбросов (экстремальное значение)

Число опытов	Доверительная вероятность Р
0.95	0.99
	0.941	0.988
	0.765	0.889
	0.642	0.780
	0.560	0.698
	0.507	0.637
	0.554	0.683

Сравните величину r ₁₀ с критическим значением (таблица 1). В случае, если r ₁₀ меньше критического значения - x ₁ не является выбросом, а если r ₁₀ больше критического значения - x ₁ является выбросом и его необходимо исключить из дальнейших расчетов.

4.1.2. Определить максимальное и минимальное значение выборки, моду, размах выборки и среднее арифметическое значение.

Определите минимальное и максимальное значение выборки x(min) и x(max).

Определите моду выборки – наиболее часто встречающееся значение выборки (обозначается ).

Определите размах выборки R=x(max)-x(min).

Определите среднее арифметическое значение выборки по формуле: ,

где: x _i – значения элементов выборки, n – количество элементов в выборке.

4.1.3. Определите выборочную дисперсию по формуле: ,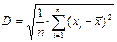

где: x _i – значения элементов выборки, n – количество элементов в выборке.

4.1.4. Определить значения верхней и нижней границ доверительного интервала для заданной доверительной вероятности.

Пользуясь таблицей 2, выпишите значение процентных точек t-распределения Стьюдента (t _n =).

Таблица 2

Процентные точки t-распределения Стьюдента.

n	Доверительная вероятность Р
0.95	0.99
	6.314	31.82
	2.920	6.965
	2.353	4.541
	2.132	3.747
	2.015	3.365
	1.943	3.143
	1.895	2.998
	1.860	2.896

Определите значения верхней 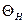и нижней 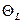границ доверительного интервала по формулам: , ,

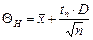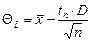где: 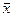- средне арифметическое значение выборки, t _n - процентные точки t-распределения Стьюдента, D – дисперсия, n – количество элементов выборки.

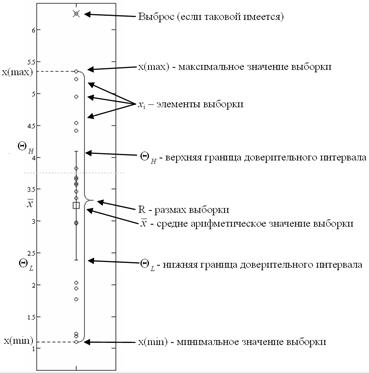
4.1.5. Отобразить на графике все элементы и характеристики выборки.

В результате проделанной работы все полученные величины необходимо нанести на график, имеющий следующий вид:

4.2.1. Определите вероятность события, при котором в выборке (n – количество элементов выборки) будет присутствовать определенное количество бракованных образцов (r – количество бракованных образцов) по формуле: ,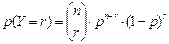

где: p – процент брака, а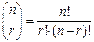

Для решения 2-го задания рассмотрим пример.

Задание: Пусть в некотором процессе получается 2% брака. Берется выборка из 10 независимых образцов. Найти вероятность того, что в этой выборке не окажется дефектов; будет не более чем один дефект.

Решение:

Вероятность того, что в этой выборке не окажется бракованных образцов определяется по формуле: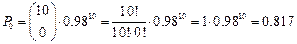

Вероятность того, что в этой выборке окажется только 1 бракованный образец определяется по формуле:

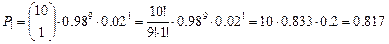
Ответ: Вероятность наличия в партии не более одного дефектного образца:

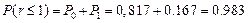
Дата добавления: 2015-04-24