Решить графически задачу линейной оптимизации функции отклика, зависящей от двух факторов

Пользуясь градиентным методом оптимизации. ручным расчетом выполнить один шаг в направлении оптимума заданной функции отклика модельной системы. Результат сопоставить с компьютерным расчетом, выполненным на лабораторном занятии.

По заданной совокупности экспериментальных точек построить адекватную регрессионную модель и выполнить идентификацию ее параметров.

4.4.1. Определите значения функциональной модели при значениях абсциссы, соответствующих значениям абсциссы экспериментальных точек.

4.4.2. Определите значение “невязок” для каждой экспериментальной точки и функциональной модели по формуле , где: Y _i – значение ординаты экспериментальной точки в соответствии с заданием. F(x _i ) – значение уравнения Y= F(x _i ) при значениях x _i, соответствующих значениям абсцисс экспериментальных точек.

4.4.3. Определите численное значение нормы Гаусса по формуле: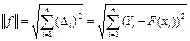

4.4.4. Определите численное значение нормы Чебышева по формуле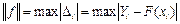

4.4.5. Постройте график, на котором нанесите функциональную модель, экспериментальные точки и рассчитанные в п. 4.2.2 “невязки”.

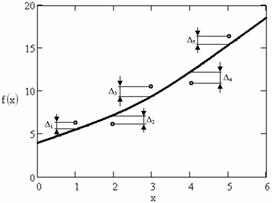
4.5.1. Определите значение функции Z₀ в точке с координатами X₀. Y₀.

4.5.2. Определите частные производные функции Z по направлениям X, Y ( и ).

4.5.3. Определите значения полученных в п. 4.3.2 частных производных в точке с координатами X₀, Y₀ (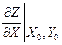 и ).

4.5.4. Определите вектор gradient в точке с координатами X₀, Y_0.

, подставив значения X₀. Y₀ необходимо записать уравнение вектора gradient таким образом, чтобы частные производные функции Z по 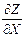и 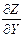приняли численные значения.

4.5.5. Сделать шаг в направлении вектора gradient из точки с координатами X₀. Y₀ в направлении max или min в зависимости от задания. (Определить значения X₁. Y₁.)

Для выполнения этого пункта рассмотрим представленный ниже рисунок.

В системе координат xoy нарисован между точками ОА₂.

При этом отрезок OB₂ соответствует численному значению , а отрезок OC₂ соответствует численному значению . Рассмотрим случай, когда требуется сделать шаг в направлении вектора gradient на величину, равную l. Тогда координаты точки, в которую мы переместимся при выполнении шага, будут определяться следующими соотношениями: и .

Определим величину . Для этого рассмотрим треугольники OA₁B₁ и OA₂B₂. Рассматриваемые треугольники являются подобными и. следовательно, справедливо следующее соотношение:

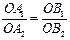или .

Следовательно, .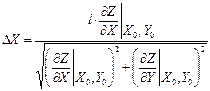

Проведя аналогичный анализ для треугольников OA₁С₁ и OA₂С₂. получим:

В случае, когда в задании требуется выполнить шаг в направлении max, т.е. в направлении вектора gradient: и .

В случае, когда в задании требуется выполнить шаг в направлении min, т.е. в противоположном относительно направления вектора gradient: и .

4.5.6. Определите значение функции Z₁ в точке с координатами X₁. Y₁.

4.5.7. Сравните значения Z₀ и Z₁. сделайте вывод о правильности сделанного шага.

4.6.1. Составьте целевую функцию в соответствии с заданным условием.

4.6.2. Составьте систему границ и ограничений, описывающих область допустимых значений целевой функции в соответствии с заданным условием.

4.6.3. Постройте график, на котором нанесите все границы и ограничения, составленные в п. 4.5.2.

4.6.4. Постройте целевую функцию с произвольным ее значением.

4.6.5. Перемещая целевую функцию параллельно самой себе в направлении оптимума, найдите точку решения.

4.6.6. В случае нецелочисленного решения определите точку решения с целыми значениями координат.

4.6.7. Определите значение целевой функции в точке решения.

Для решения 6-го задания рассмотрим пример.

Исходные данные:

Предприятие выпускает два типа изделий: стулья и кресла.

Отпускная цена одного стула – 10 руб., одного кресла – 15 руб.

Для обивки одного стула используют 1м² ткани, одного кресла – 2м² ткани.

На складе в наличии 102м² обивочной ткани.

Для покрытия лаком одного стула расходуется 15см³ лака, для покрытия одного кресла 3см³ лака.

На складе в наличии 450см³ лака.

На складе имеется 25 комплектов деталей, используемых для изготовления стульев, и 45 комплектов деталей для изготовления кресел.

Задание: Какое количество стульев и кресел следует изготовить на предприятии, чтобы получить максимальную стоимость продукции?

Решение:

1. Обозначим искомое количество стульев – X₁, а искомое количество кресел - X₂.

2. В соответствии с текстом задания сформируем целевую функцию, позволяющую определить максимальную стоимость продукции. Учитывая, что за один стул, возможно, выручить 10 руб. то за X₁ стульев 10×X₁. За одно кресло предприятие может выручить 15 руб. следовательно, за X₂ кресел 15×X₂.

Окончательно целевая функция будет иметь вид:

Ц.Ф.

3. Сформируем систему ограничений, задающих область допустимых решений.

3.1. Ограничение по ткани. Данное ограничение показывает, что при расходе ткани при производстве каждого стула в количестве 1м², а при производстве каждого кресла 2м². общее количество расходуемой ткани не должно превысить 102м², имеющихся на складе.

3.2. Ограничение по лаку. Данное ограничение показывает, что при расходе лака при производстве каждого стула в количестве 15см³. а при производстве каждого кресла 3см³. общее количество расходуемого лака не должно превысить 450см³, имеющихся на складе.

3.3. Ограничение по количеству комплектов деталей, имеющихся на складе. Здесь необходимо предусмотреть 4 ограничения, показывающих, что невозможно изготовить такое количество стульев и кресел, которое будет превышать количество имеющихся на складе комплектов деталей. Кроме того, следует математически записать невозможность изготовления отрицательного количества стульев и кресел. . . .

3.4. Нарисуем в произвольном масштабе систему координат, в которой горизонтальная ось будет задавать количество стульев (X1). а вертикальная ось - количество кресел (X2). В данной системе координат нарисуем все границы и ограничения, предварительно знаки £ и ³ на =: , , , , ,

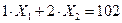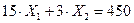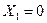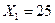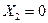В таком виде все уравнения представляют собой уравнения прямых линии и их легко нарисовать, определив точки их пересечения с осями координат. Пересечение границ и ограничений обозначим точками Р₁. Р₂. Р₃. Р₄. Р₅ и Р₆.

3.5. Нарисуем целевую функцию внутри области допустимых значений. Для этого заменим уравнение Ц.Ф. на и приравняем p к произвольному целому числу. В нашем случае p=300.

Для отыскания требуемого решения нарисованную целевую функцию будем перемещать параллельно самой себе вправо и вверх для отыскания max или влево и вниз для отыскания min.

Как видно из рисунка приведенного ниже, максимальное значение целевой функции, при котором она не покинет область допустимых значений будет в точке P₃.

Данная точка образована пересечением двух ограничений: . Решив данную систему уравнений, получим координаты , , 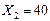а подставив эти значения в целевую функцию, найдем решение поставленной задачи (820 руб.).

Ответ: Максимальную стоимость продукции предприятия в размере 820 рублей можно получить в случае изготовления 22 стульев и 40 кресел.

Литература.

1. Мельников А.С., Шевцов С.Н. Математическое моделирование в технологии и проектировании. Интерактивный учебный курс http://de.dstu.edu.ru (http://static.dstu.edu.ru/aireng/ru/resources/metod%20razrab.html)

2. САПР: Системы автоматизированного проектирования. В 9 кн. Кн.4. Математические модели технических объектов. под ред. И.П. Норенкова.- М.: Высш. шк.. 1986

3. Робототехника и гибкие автоматизированные производства. В 9 кн. Кн.5. Моделирование робототехнических систем и гибких автоматизированных производств. под ред. И.М. Макарова.- М.: Высш. шк., 1986

4. Лебедев А.Н. Моделирование в научно-технических исследованиях.- М.: Радио и связь, 1989

5. Шакалис В.В. Моделирование технологических процессов.- М.: Машиностроение, 1973

6. Советов Б.Я., Яковлев С.А. Моделирование систем.- М.: Высш. шк., 1985

7. Джонсон Н., Лион Ф. Статистика и планирование эксперимента в технике и науке. Т.1. Методы обработки данных., Т.2. Планирование эксперимента. М.: Мир, 1977

8. Д.Гроп Методы идентификации систем. М. «Мир», 1977.

9. Хан Г., Шапиро С. Статистические модели в инженерных задачах.- М.: Мир, 1969.

Дата добавления: 2015-04-24