Теорема 12.5. Определение 8.3, т.е. определение предела по Коши, равносильно определению 12.3 предела по Гейне

Доказательство достаточности значительно труднее и его не обязательно рассказывать на экзамене.

Однако для заинтересованного читателя ниже приводится схема этого доказательства.

Сначала дадим ещё одно определение предела функции при .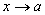

Определение 12.3 (предела функции при 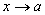по Гейне). Говорят, что функция имеет при 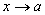предел 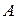, если для любой последовательности такой, что 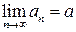и такой, что для всех выполнено неравенство 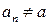, предел .

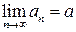◄ Пусть сначала функция имеет предел по Коши. Рассмотрим произвольную последовательность такую, что и такую, что для всех выполнено неравенство 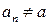. По определению предела по Коши, 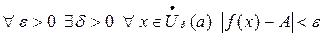. По определению предела последовательности, . Значит, при выполняется условие , из которого сразу следует неравенство , означающее, что , Тем самым, предел этой функции по Гейне также существует.

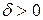Предположим теперь, что предел по Коши не существует и докажем, что не существует и предел по Гейне. По предположению, существует такое число , что для любого числа существует такая точка , что . Последовательно выбирая в качестве 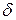числа , находим точки такие, что . Эти точки представляют собой последовательность точек, удовлетворяющую всем условиям, входящим в определение предела по Гейне, однако для этой последовательности условие не выполнено.►

Докажем теперь, что из условия (1) вытекает, что функция имеет предел по Гейне.

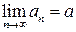Действительно, возьмём любую последовательность такую, что и такую, что для всех выполнено неравенство 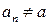. Рассмотрим соответствующую последовательность 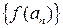. Зафиксируем и выберем соответствующее 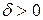с помощью (1). Так как 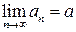, имеем: . Далее, при и,по условию (1), . Значит, 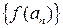-фундаментальная последовательность. По теореме 12.3 существует предел последовательности 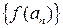, обозначим его .

Осталось доказать, что если взять любую другую последовательность такую, что и такую, что для всех выполнено неравенство , то .

Для этого рассмотрим последовательность . Это – последовательность точек, сходящаяся к точке и не принимающая значение , согласно своему определению. Поэтому последовательность значений 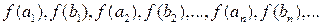также имеет предел, по доказанному выше. Тогда по теореме 12.1 предел этой последовательности равен пределу подпоследовательности и пределу подпоследовательности 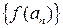, равному .►

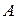Дата добавления: 2015-04-24