Метод наименьших квадратов. В различных исследованиях приходится пользоваться формулами, составленными на основании эксперимента

В различных исследованиях приходится пользоваться формулами, составленными на основании эксперимента. Одним из лучших способов получения формул является метод наименьших квадратов.

Пусть на основании эксперимента необходимо установить функциональную зависимость между переменными величинами x и y, например, между температурой и удлинением прямолинейного металлического стержня. Производим n измерений, по результатам составляем таблицу

X	x1	x2	…	xi	…	xn
Y	y1	y2	…	yi	…	yn

При этом вид функции устанавливается из теоретических исследований, или по характеру положения на координатной плоскости экспериментальных точек. Пусть, например, точки, взятые из таблицы, расположены так, как показано на рис. 45. В данном случае естественно предположить, что между 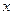и существует линейная зависимость, выражающаяся формулой

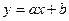(1)

Мы ограничимся рассмотрением случая линейной зависимости.

Так как точки (x₁;y₁),(x₂;y₂),…,(x_n;y_n) приблизительно лежат на одной прямой, то формула (1) является приближенной. Поэтому, подставляя их координаты в формулу (1) вместо 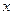и получим следующие равенства: ,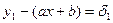
,
………………,
.

где некоторые числа, которые назовем погрешностями.

Возникает задача – подобрать коэффициенты 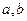таким образом, чтобы эти погрешности были возможно, меньше по абсолютной величине. Методом решения этой задачи и является метод наименьших квадратов. Согласно этому методу рассмотрим сумму квадратов погрешностей:
.

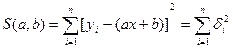где 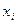и 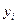- заданные числа, а коэффициенты 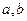– неизвестные величины, подлежащие определению, т.е. можно рассматривать как функцию двух переменных 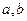и исследовать ее на экстремум.

Имеем
,
.

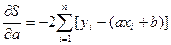Приравнивая эти частные производные нулю, получаем линейную систему двух уравнений с двумя неизвестными :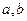

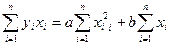(2)

Система (2) называется нормальной системой метода наименьших квадратов. Из нее мы находим числа 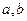, подставляя их в уравнение (1), получаем форму искомой прямой.

Во – первых, для разрешимости системы (2) потребуется условие

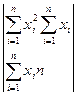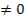= (3)

Лемма. Величина в правой части (3) равна и, следовательно, больше 0.

Доказательство. Правая часть этого равенства равна

Эту сумму легко сгруппировать и получить .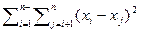

Итак, такие a, b, чтобы выполнялась система (2), существуют. Чтобы проверить, что в этих точках функция S(a,b) действительно имеет минимум, вычислим 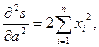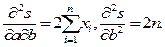. Следовательно, определитель

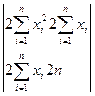, по лемме имеет положительные главные миноры, поэтому найденная точка – точка минимума.

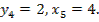
Пример. Пусть в результате эксперимента получены пять значений искомой функции у при пяти значениях аргумента х (n=5), которые записаны в таблице: дем искать функциональную зависимость между x и y в виде линейной функции y=ax+b.

При составлении нормальной системы (2) для определения коэффициентов a и b, вычисляем

Система (2) принимает вид

25a+5b=16,5,

5a+5b=8.

Решая эту систему, находим: a=0,425,b=1,175. Отсюда формула искомой прямой есть

y=0,425x+1,175.

Дата добавления: 2015-04-24