Ортогональное планирование для трехфакторной модели

Уравнение регрессии для трехфакторного эксперимента имеет следующий вид (математическая модель второго порядка):

Y=b₀+b₁x₁+b₂x₂+b₃x₃+b₁₁x₁²₊b₂₂x₂²+b₃₃x₃²+b₁₂x₁x₂+b₁₃x₁x₃+b₂₃x₂x₃ (1)

Общее количество опытов рассчитывается по формуле:

N=N₀+2k+n₀, (2)

где n₀ – количество опытов в центре плана, k – число факторов, N₀ – число опытов полного факторного эксперимента 2^k.

Количество точек проводимых опытов в области планирования равно N=8+2·3+1=15. Значение «звездного плеча» равно α=±1,21.

Составим матрицу для расчетов коэффициентов.

Таблица - Матрица для расчетов коэффициентов уравнения регрессии для трехфакторного эксперимента

Номер опыта	Матрица для расчета коэффициентов	Экспериментальные значения y
x0	x1	x2	x3	(x1')^2	(x2')^2	(x3')^2	x1x2	x1x3	x2x3
		-1	-1	-1	0,27	0,27	0,27				0,45
			-1	-1	0,27	0,27	0,27	-1	-1		0,42
		-1		-1	0,27	0,27	0,27	-1		-1	0,26
				-1	0,27	0,27	0,27		-1	-1	0,27
		-1	-1		0,27	0,27	0,27		-1	-1	0,56
			-1		0,27	0,27	0,27	-1		-1	0,57
		-1			0,27	0,27	0,27	-1	-1		0,37
					0,27	0,27	0,27				0,36
		-1,21			0,74	-0,73	-0,73				0,36
		1,21			0,74	-0,73	-0,73				0,39
			-1,21		-0,73	0,74	-0,73				0,47
			1,21		-0,73	0,74	-0,73				0,21
				-1,21	-0,73	-0,73	0,74				0,31
				1,21	-0,73	-0,73	0,74				0,46
					-0,73	-0,73	-0,73				0,37
Сумма квадратов ∑		10,94	10,94	10,94	4,34	4,34	4,34				5,83

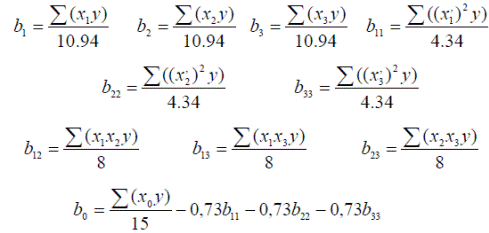Для полного факторного эксперимента коэффициенты уравнения (1) рассчитываются по следующим формулам:

(3)

Рассчитав коэффициенты b по формуле (3), получили следующие значения:

Таблица – значения коэффициентов b

b1	0,00149
b2	-0, 0964
b3	0, 05864
b11	0, 02456
b22	0, 00085
b33	0, 031336
b12	0, 0025
b13	0, 0025
b23	0,0075
b0	0,347238

В результате расчета было получено следующее уравнение регрессии:

Y(x₁x₂)=0,347238+0,00149x₁-0,0964x₂+0,05864x₃+0,02456x₁²+0,00085x₂²+ +0,031336x₃²+0,0025x₁x₂+0,0025x₁x₃-0,0075x₂x₃

После этого проверяем значимость коэффициентов с помощью критерия Стьюдента по формулам:

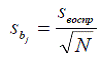(4)

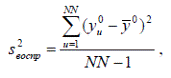(5)

где NN -количество параллельных опытов;

формула (5) - дисперсия воспроизводимости;

ӯ⁰ -среднее значение величины у, полученных при параллельных опытах;

у_u⁰ - значения, полученные при постановке каждого из дополнительных опытов в центре плана.

Sb_j=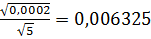

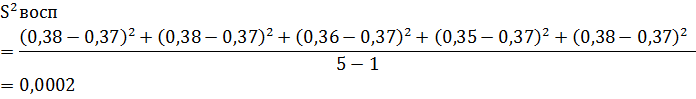
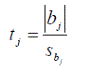Расчетное значение коэффициента Стьюдента определяется по формуле:

(6)

Если полученное расчетное значение доверительного интервала меньше табличного, то данные коэффициенты исключаются из уравнения регрессии. Табличное значение критерия Стюдента для уровня значимости р=0,05 и числа степеней свободы f=2 t_p(f)=4,3.

Выполнив расчеты по формуле (6), получим следующие коэффициенты:

Таблица - коэффициент Стьюденса

t1	0,2356	коэффициент не значим
t2	15,2411	коэффициент значим
t3	9,2711	коэффициент значим
t11	3,8830	коэффициент не значим
t22	0,1344	коэффициент не значим
t33	4,9543	коэффициент значим
t12	0,3953	коэффициент не значим
t13	0,3953	коэффициент не значим
t23	1,18577	коэффициент не значим
t0	54,8993	коэффициент значим

Проверяем адекватность полученного уравнения регрессии, используя критерий Фишера:

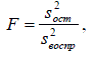
(7)

где 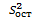- остаточная дисперсия, рассчитывается по формуле:

(8)

L - число значимых коэффициентов в уравнении регрессии.

S²_ост= 0,013616

Табличное значение коэффициента Фишера для р=0,05, f₁=14 и f₂=4 F_1-p(f₁,f₂)=3,1

Если расчетное значение критерия Фишера больше табличного, то полученное уравнение регрессии неадекватно описывает эксперимент.

F= ,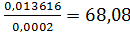

68,08>3,1, следовательно, полученное уравнение регрессии неадекватно описывает эксперимент.

Так как коэффициенты b₀, b₂, b₃ и b3₃ больше табличного значения критерия Стюдента, то их следует оставить в уравнении, а остальные исключить. Вследствие чего уравнение регрессии примет вид:

Y=0,347238-0,0964x₂+0,05864x₃+0,031336x₃²

Дата добавления: 2015-04-24