Основная теорема теории игр

Методы решения матричных игр в смешанных стратегиях основаны на основной теореме теории игр: любая конечная матричная игра имеет оптимальное решение, хотя бы одно.

Для решения важны следующие следствия:

1. Если игрок А придерживается своей оптимальной смешанной стратегии, то независимо от поведения игрока В он получит выигрыш не менее V (равным V, если второй игрок также придерживается оптимальной смешанной стратегии), т.е.

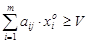. (8)

2. Если игрок В придерживается своей оптимальной стратегии, то он получит проигрыш не больший V или равный V, если игрок А придерживается своей оптимальной стратегии, т.е.

. (9)

3 и 4. Сумма вероятностей применения игроками своих оптимальных «чистых» стратегий равна 1, т.е.

,

.

Данная система уравнений и неравенств составляется и решается для нахождения .

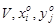Графический способ решения применяется для игровых моделей размерности . Игровые модели любой размерности могут быть решены путем их приведения к основной ЗЛП (ОЗЛП). Реализация этого метода предполагает некоторые преобразования системы неравенств, составленной по основной теореме теории игр.

Во-первых, это прибавление положительного числа C =const ко всем элементам платежной матрицы, если не все элементы больше или равны нулю, что гарантирует положительность значений модифицированной игры. Истинное значение (цена) игры в этом случае меньше найденного после решения основной задачи линейного программирования (ОЗЛП) на величину С.

Во-вторых, введение новых переменных: для игрока А: ; для игрока В: 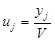. Путем разделения правой и левой частей неравенств (8) и (9) на V, получаем две системы неравенств для игроков А и B соответственно (10) и (11)

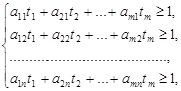
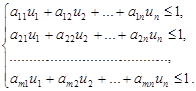
Тогда постановка ОЗЛП для нахождения оптимальной смешанной стратегии игрока А может быть осуществлена следующим образом:

- найти такие , при которых достигается минимум целевой функции , и выполняется система ограничений (10).

Постановка ОЗЛП для игрока В:

- найти такие , при которых достигается максимум целевой функции , и выполняется система ограничений (11).

После решения этих задач осуществляется переход к исходным переменным 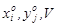с использованием соответствующих преобразований. Эти задачи представляют собой пару двойственных задач линейного программирования и могут быть решены с использованием симплекс-метода.

Дата добавления: 2015-04-24