Формула полной вероятности

Сложение вероятностей совместимых событий

Вероятность суммы двух совместимых событий A и В равна сумме вероятностей этих событий минус вероятность их произведения:

Р(А + В) = Р(А) + Р (В) — Р(АВ).

Вероятности попадания в цель при стрельбе пер­вого и второго орудий соответственно равны: Р(А)=0,7 и Р(В)=0,8. Найти вероятность попадания при одном залпе (из обоих орудий) хотя бы одним из орудий.

Очевидно, события А к В совместимы и независимы. Поэтому

Р (А + В) =Р (А) +Р (В) - Р (АВ) = 0,7 + 0,8 - 0,7* 0,8 = 1,5 — 0,56 = 0,94.

Замечание. Если события А и В несовместимы, то их произведение АВ есть невозможное событие и, следовательно, Р (АВ) = 0.

Вероятность события А, которое может наступить лишь при условии появления одного из n попарно несовместимых событий В₁, В₂,..., В_n образующих полную группу, равна сумме произведений вероятностей каждого из этих событий на соответ­ствующую условную вероятность события А:

Р (А) = Р (В₁) P_B1 (А) + Р (В₂)Р_В2 (А) +... + Р (Вn)Р_Bn(А)

Имеются три одинаковых по виду ящика. В пер­вом находятся две белые мыши и одна серая, во втором — три бе­лые и одна серая, в третьем — две белые и две серые мыши. Какова вероятность того, что из наугад выбранного ящика будет извлечена белая мышь?

Обозначим В₁ — выбор первого ящика, В₂ — выбор второго ящика, B₃ — выбор третьего ящика, А — извлечение белой мыши.

Так как все ящики одинаковы, то Р (B₁)= Р (B₂) = Р (B₃) = 1/3.

Если выбран первый ящик, то Рв₁ (А) = 2/3. Аналогично Рв₂ (А) =3/4, Рв₃(А) = 0,5. Наконец, по формуле получаем:

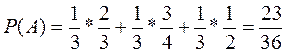
В группе студентов 4 отличника, 13 хорошо успевающих и 8 слабых студентов. Результаты предшествующих экзаменационных сессий показали, что отличники получают только отличные оценки (потому они и отличники); «хорошисты», как правило, в девяти случав из десяти получают отличные или хорошие оценки; наконец слабые студенты в одном случае из пяти получают хорошие оценки.

Для сдачи экзамена выбирается один студент. Найти вероятность события А, что студент получит хорошую или отличную оценку.

Дата добавления: 2015-04-24