Интегрирование элементарных рациональных дробей четырех типов

Способы вычисления коэффициентов при разложении рациональной дроби на элементарные.

Пример.

Теперь надо приравнивать многочлены в числителях дробей и определять неизвестные коэффициенты A, B, M, N, P, Q.

Это можно сделать двумя способами.

1 способ – приравнивать коэффициенты при одинаковых степенях переменной, составлять и решать систему уравнений.

X⁵| 3=A+B+M

X⁴| 1=A-B+N

X³| 7=2A+2B+P

X²| 2=2A-2B+Q Решение системы A=2, B=1, M=N=Q=0, P=1.

X |2=A+B-N-P

1 |1=A-B-N-Q

2 способ – задавать значения неизвестной, вычислять значения числителей и составлять систему уравнений.

X=1 | 16=8A

X= -1| -8=-8B

X=0 | 1=A-B-N-P

X=2 | 181=75A-25B+30M+15N+6P+3Q

X=-2 | -96= -25A-75B-30M+15N-6P+3Q

X=-3 | -824= -200A –400B-240M –80N –24P+8Q

Решая эту систему уравнений, получим то же решение A=2, B=1, M=N=Q=0, P=1.

Какой способ применять – зависит от того, где получается более простая и удобная для решения система уравнений.

В данном примере вторая система сложнее первой.

1) ,

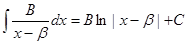2)

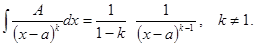
3) =

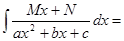
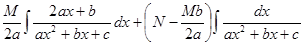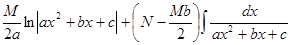(пример рассмотрен во второй лекции). Для того, чтобы вычислить интеграл от дроби в п.3, достаточно в соответствующем примере второй лекции обозначить коэффициенты другими буквами.

4) = =

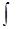
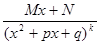
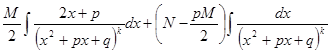, где .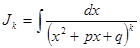

Вычислим интеграл .

.=

- =

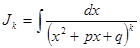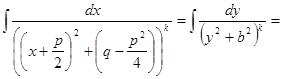
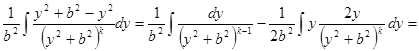
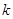По этой рекуррентной формуле можно последовательно вычислять интегралы при различных , предварительно вычислив

.

Таким образом, показано, что все четыре типа элементарных рациональных дробей интегрируемы. Следовательно, класс рациональных функций представляет собой класс интегрируемых функций.

При интегрировании конкретных рациональных функций выделяют целую часть и раскладывают рациональную дробь на элементарные. Затем интегрируют элементарные рациональные дроби.

Пример.

Составляем и решаем систему уравнений относительно неопределенных коэффициентов (первый способ определения коэффициентов)

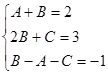Получим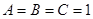

Можно воспользоваться и вторым способом определения коэффициентов.

X=0 | -1 = B-A-C

X=1 | 4 = A+B+2B+C+B-A-C= 4B

X=-1| -2 = A+B-2B-C+B-A-C= -2C. Отсюда C=1, B=1, A=1.

Вторая система проще, чем первая.

Теперь интегрируем сумму элементарных дробей.

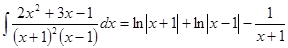
Дата добавления: 2015-04-24