Многофакторные эколого-математические модели. Анализ влияния отдельных факторов в экологической модели

Лекция 7.

В практике часто возникают ситуации, когда функция отклика
(цели) У зависит не от одного, а от многих факторов. Установление
формы связи в этих случаях начинают, как правило, с рассмотрения линейной регрессии вида

В этом случае результаты наблюдений должны быть представлены

уравнениями, полученными в каждом из и опытов:

или в виде матрицы результатов наблюдений

где n — количество опытов; k — количество факторов.

Для решения систем уравнений необходимо, чтобы количество
опытов было не менее (k+1), т.е. n > k+l.

Задачей множественного регрессионного анализа является пост-
роение такого уравнения прямой в k-мерном пространстве, откло-
нения результатов наблюдений х_ij от которой были бы минималь-
ными. Используя для этого метод наименьших квадратов, получаем
систему нормальных уравнений

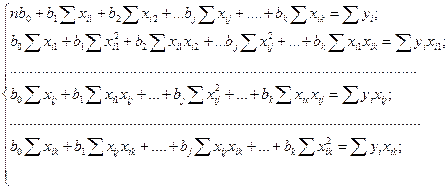
В матричном виде

,

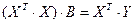где В — вектор-столбец коэффициентов уравнения регрессии;

Х — матрица значений факторов;
Y — вектор-столбец функций отклика;
Х^T — транспонированная матрица Х Они соответственно равны:

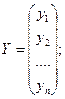
при х_j0 = 1, j =1,n;

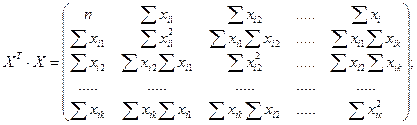
Умножая правую и левую части уравнения на обратную матри-
цу (Х^T∙Х)^-1, при (Х^T∙Х)^-1∙(Х^T∙Х)^-1= Е = 1 получим:

(Х^T∙Х)^-1(Х^T∙Х)В= (Х^T∙Х)^-1(Х^T∙Y).

Откуда В= (Х^T∙Х)^-1(Х^T∙Y). Каждый коэффициент уравнения
регрессии вычисляется по формуле

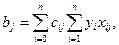
где с_ij — элементы обратной матрицы (Х^T∙Х)^-1.

Пример. В результате проведенных исследований влияния мощ-
ности гумусового слоя почвы (Х₁) и количества внесенного слож-
ного состава минерального удобрения (Х₂) на урожайность зерно-
вой культуры (Y) получены уравнения:

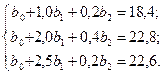
Установить форму связи урожайности е факторами х ₁и х ₂в
виде линейного уравнения регрессии.

Р е ш е н и е. Представляем результаты опытов в виде матриц:

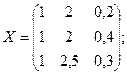
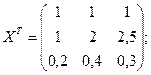
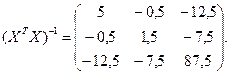
Определяем коэффициенты уравнения регрессии

Отсюда b₀ = 14, b₁ = 2, b₂ = 12 и уравнение регрессии имеет вид

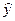=14+2х₁ +12х₂.

Для проверки значимости уравнения регрессии необходимо при заданных значениях (х₁,х₂) провести несколько экспериментов, чтобы для данного значения (х₁,х₂) получить
некоторое среднее значение функции у. В этом случае экспериментальный материал представляется, например, в виде
табл. 7.1.

Таблица 7.1

Дата добавления: 2015-04-24