Метод Лагранжа

Методы оптимизации. Метод Лагранжа

Лекция 9.

Анализ влияния отдельных факторов в экологической модели.

Лекция 8.

(Самостоятельно – Гринин А.С., Орехов Н.А., Новиков В.Н. Глава 3§3.6.) Некоторые особенности применения экспериментально-статистических методов в экологии. Проверка статистических гипотез при планировании экспериментов.

В экологии часто встречаются объекты исследования, состояние
которых определяется факторами, не имеющими количественной
оценки. Такими факторами могут быть неуправляемые и управляемые переменные, которые по каким-либо причинам не позволяют
производить их измерение в данном эксперименте, а также те не-
контролируемые переменные, уровни варьирования которых можно
произвольно выбирать и фиксировать по времени.

Для изучения влияния факторов подобного рода на функцию
отклика Y (целевую функцию), их общего оценивания, ранжирования и выделения среди них существенных, методы регрессионного
анализа непригодны, поскольку они решают задачи определения
вида математической модели при варьировании величиной факторов. Здесь целесообразно использовать методы дисперсионного анализа.

назад

Оптимизация играет важную роль при экологических исследованиях и поиске наилучших характеристик объекта или наименьших затрат ресурсов.

Оптимизации подвергается целевая функция, которая в этом
случае выражается через какие-либо параметры (факторы), при не-
которых заданных ограничениях. В общем случае задача оптимизации формулируется следующим образом: найти значения параметров х ₁, х ₂,..., х _n, при которых целевая функция

Y= f (х ₁, х ₂ ,..., х _n)

принимает максимальное (минимальное) значение при функциональных ограничениях, выражаемых в виде равенств

F ₁ =f ₁(х ₁, х ₂ ,..., х _n)

F ₂ =f ₂(х ₁, х ₂ ,..., х _n) (9.1)

………………………..

F _m =f _m(х ₁, х ₂ ,..., х _n)

и областных ограничений в виде неравенств

Ф₁=φ₁(х ₁, х ₂ ,..., х _n) ≤ b₁
Ф₂=φ₂(х ₁, х ₂ ,..., х _n) ≤ b₂

……………………… (9.2)

Ф_p=φ_p(х ₁, х ₂ ,..., х _n) ≤ b_p

Для решения таких задач могут быть использованы методы: диффуренциро-ваия, множителей Лагранжа, численные методы, математическое программирование и др.

При оптимизации методом дифференцирования оптимум находится приравниванием частных производных целевой функции и затем из решений совместной системы n-уравнений находится значение всех переменных х _i.

i=

Пример. Стоимость продукта зависит от степени его очистки х, ма-
териалов на очистку k₁ и затрат труда k₂ что выражается зависимостью

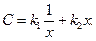
При этом чистота продукта (х) изменяется в пределах от 25%
до 90%, а имеющиеся средства на очистку равны , где 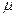— максимальная сумма денежных средств.

Требуется найти такое значение х, при котором затраты С ми-
нимальны.

Р е ш е н и е. Находим производную

Откуда

.

Это оптимальное значение получено без учета ограничений
25% < х < 90% и . Если они при этом удовлетворяются, то
обычно решение находится путем использования в качестве ограничения соответствующего предельно допустимого значения, т.е. для
нашего примера нижнего (25%-ного) или верхнего(90%-ного) уровня. При наличии функциональных ограничений их обычно можно
использовать до начала дифференцирования для уменьшения числа
параметров и, таким образом, основная задача не меняется.

Метод множителей Лагранжа используется, когда целевая функция находится при функциональных ограничениях. Задача решается следующим образом.

Оптимизировать целевую функцию

Y= f(х ₁, х ₂,..., х _n) (9.3)

при ограничениях

Ф₁= φ₁(х ₁, х ₂,..., х _n) = 0

Ф₂= φ₂(х ₁, х ₂,..., х _n) = 0

………………………. (9.4)

Ф_m= φ_m(х ₁, х ₂,..., х _n) = 0.

Дифференцируя целевую функцию, найдем ее дифференциал и
приравняем его кнулю

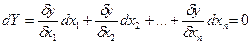
Дифференцируем каждые т ограничений

……………………..

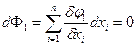
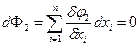
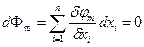
Умножаем каждое из т уравнений (9.4) на неизвестный
параметр λ_i, i= 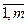, называемый множителем Лагранжа. Эти множители различны для разных уравнений.

Имеем

……………………

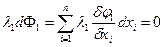
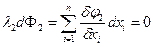
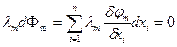
Если теперь сложить вместе все эти уравнения, прибавив уравнение dY, то получим:

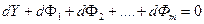
или

Поскольку все параметры х_i независимы, чтобы это уравнение
удовлетворялось, каждый из n заключенных в скобки членов предыдущего уравнения должен равняться нулю. Отсюда получим n
уравнений вида:

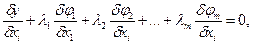i=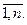

Имеется также m уравнений. Таким образом, имеется всего (n +
m) уравнений с (n + m) неизвестными: n неизвестных х_i, и т неиз-
вестных 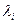. Решение этой системы даст искомое оптимальное реш
ение.

Пример. Требуется построить цилиндрический резервуар емкостью 10м³ при наименьшем расходе материала. Таким образом, целевой функцией является площадь поверхности А= 2πr²+ 2 πrl, где r —
радиус цилиндра; l — высота цилиндра. Функциональное ограничение V= πr² l = 10м³.

Р е ш е н и е. Находим производные

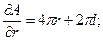
Уравнение ограничения :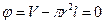

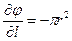
Отсюда получим три уравнения

,

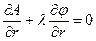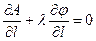
определяющих три неизвестных r, l и 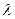, т.е.

4πr+2πl+λ(-2πl)=0;

-2πr+ λ(πr²)=0;

V= -πr² l = 0

Решая уравнения, получим:

λ = 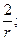l =2r; r=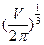

при V= 10м³; r = 1,167м; l = 2,334м.

назад

Дата добавления: 2015-04-24