Численные ошибки использованных для вычисления данных

Степень много- члена	Аппроксимация dT/dz при z =2	Порядок остаточного члена	Численное значение (dT/dz)z 0 = 0
	(Т 1 — Т 0 ) / h	h	4,12
	(-Т2 + 4Т1 — 3Т 0 ) / 2 h	h^2	4,71
	(-2 Т 3 - 9T2 + 18 Т 1 - 11 T 0)/6h	h^3	5,25
4	(-3T 4 + 16Т3 - 36Т2+ 48Т 1 - 25T 0 )/12h	h^4	3,47

Здесь аппроксимация градиента d/Т/dz и «порядок ошибки» маскируют значительно более важный источник ошибки при вычислении dT/dz, а именно случайную ошибку, порождаемую измерением.

Предположим, что все величины Т_i в табл. 12.4 обладают одинаковым стандартным отклонением 0,01 (1% от Т₀) или дисперсией в
10^-4. Тогда для многочлена четвертого порядка

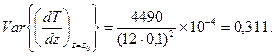
при измерениях: T _o =- 1,000; Т ₁= - 0,588; Т ₂ =- 0,295; Т ₃ =- 0,259; T ₄=-0,305; h = 0,1.
Тогда , что составляет около 16% от .

Оценивание методом наименьших квадратов. Если наблюдения Y
для откликов модели представляют собой непрерывные функции
времени в интервале от t = 0 до t = t_i то МНК требует минимизировать величину

,

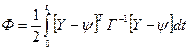где Г — ковариационная матрица;

Ф — проинтегрированное по времени значение квадрата ошибки.
Если наблюдения производились в дискретные моменты времени t _i,
i= 1, 2,..., n, то, согласно критерию Маркова, следует минимизировать величину

.

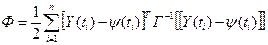Если матрица Г является диагональной, то Ф соответствует критерию «взвешенных наименьших квадратов». Если же Г = получается критерий «обыкновенных наименьших квадратов».

Величина ψ в общей форме

ψ (α,у₀,t_i) = Y(t_i) - ε(t_i),

ε(t_i) = Y(t_i) - ψ (t_i).

т.е.

Для минимизации дифференцируем функцию Ф по у₀ и α.

Приравниваем ее нулю

Подобную систему уравнений можно получить и для непрерывных данных, заменяя суммы по дисперсионным значениям на интегралы по времени. Для получения оценки точност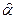и и 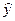необходимо сделать
некоторое предположение относительно распределения ненаблюдаемых ошибок, например, постулировать нормальное совместное распределение.

Чтобы получить оценки точности 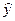, решение модели необходимо приближенно представить в виде линейной функции параметров, разлагая это решение в ряд относительно оценок этих
параметров линеаризацией.

Пример. Пусть имеем модель

.

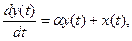
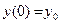Тогда

.

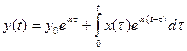Дифференцируя

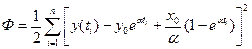
по у₀ а затем по α и заменяя в получившихся выражениях у₀ и α на их оценки получим:

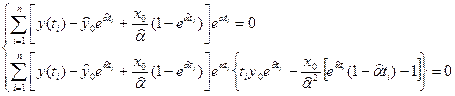
Используя функцию Ф следует учитывать:

1) ненаблюдаемая ошибка добавляется к детерминированному отклику специальным образом;

2) в оценках используются одновременно все n откликов;

3) в критерии не входит никакая априорная статистическая
информация, за исключением, быть может, той, которая вводится
с помощью матрицы Г.

назад

Дата добавления: 2015-04-24