Модели процессов содержащие обыкновенные дифференциальные уравнения

Лекция 12.

Многие экологические процессы развиваются во времени и
представляют собой динамические процессы, которые характеризуются изменением скорости течения. Такие процессы могут
рассматриваться с точки зрения оценивания состояния системы
в заданные моменты времени.

Определение состояния процесса означает оценивание зависимых переменных этого процесса. Можно различить три типа
оценивания состояния. Если проведены наблюдения в интервале
от t ₀до t_i, то оценивание вектора состояния в момент времени t
классифицируется как:

1) интерполяция (сглаживание), если t < t_i;
2) фильтрация, если t = t_i;
3) экстраполяция (предсказание), если t > t_i.

Если модель процесса представляет собой дифференциальное уравнение, то эксперименты следует проводить по планам, которые должны давать независимые ошибки при измерениях, а модель, коэффициенты которой требуется оценить, должна быть адекватной.

Модель должна содержать: дифференциальные уравнения и граничные и(или) начальные условия. Последние необходимы для
того, чтобы модель имела единственное решение.

В модели с начальными значениями, содержащей одно дифференциальное уравнение, число задаваемых начальных условий
должно равняться порядку наивысшей производной. Для системы дифференциальных уравнений первого порядка обычно задается по одному начальному условию на зависимую переменную в
каждом уравнении.

В модели с граничными значениями соответствующее число
значений зависимой переменной или ее производных задается
при различных значениях независимых переменной, т.е. не только в начале, но и в конце интервала изменения независимой
переменной. Если общее решение модели известно, заданные
значения можно подставить в общее решение и вычислить произвольные постоянные.

Простейшей моделью является обыкновенное дифференциальное
уравнение первого порядка с постоянным коэффициентом

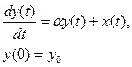
которое имеет решение

,

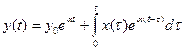где τ — переменная интегрирования;

α — коэффициент;

у — зависимая переменная, которая называется состоянием
системы;

t — независимая переменная, которая может быть не только
временем;

у₀ — не зависящее от времени начальное условие;

x(τ) — детерминированная входная функция (возмущающая сила).

Для того чтобы получить наблюдаемую зависимую переменную
Y(t), к функции у(τ) следует добавить ненаблюдаемую ошибку ε(t).
Для дискретных наблюдений

Y(t_i) = y(t_i)+ ε(t _i),

а для непрерывных переменных

Y(_i) = y(t)+ ε(t)

Если параметр, αзаменить его оценкой 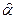, то остаточная ошибка
определяется

Е(t) = Y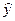(t) - (t).

Целью оценивания параметров является получение значения параметра, а в процессе наблюдений Y(t_i) и Y(t). Чтобы сделать это,
необходимо знать функцию х (t) и иметь некоторую информацию о
характере ε(t).

Более общей является модель, содержащая систему линейных
обыкновенных дифференциальных уравнений первого порядка с
постоянными коэффициентами (рис. 12.6)

.

Рис. 12.6. Многомерный процесс с несколькими входами

В матричной форме модель имеет вид:

, .

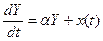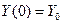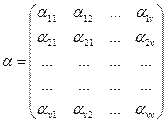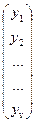; Y= ; Х = .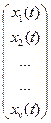

Тогда решение можно записать в форме

.

Модель, содержащую одно или несколько линейных дифференциальных уравнений более высокого порядка с постоянными
коэффициентами, например

,

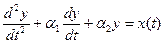можно преобразовать в модель, содержащую систему обыкновенных дифференциальных уравнений первого порядка, следующим
образом. Введём обозначения

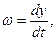
Тогда уравнение второго порядка будет представлено в виде
двух уравнений первого порядка

, ,

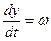однако функция, а в действительности является производной.

Общая нелинейная модель первого порядка имеет вид

,

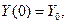
где F (α ,Y,t)представляет собой весьма общую нелинейную функцию. Уравнение, за редким исключением, не имеет аналитического решения и его следует решать численными методами.

Вследствие трудностей получения аналитических решений для
детерминированной модели процесса

эксперименты должны быть поставлены так, чтобы измерялся вектор производных dy/dt а не сам вектор Y. Если наблюдаемой
переменной является производная, то процедура оценивания вообще не затрагивает дифференциального уравнения; параметры и начальные условия можно оценить методами регрессионного анализа.

Другой способ (менее удовлетворительный) позволяет избежать операций с производными при оценивании. Он состоит в использовании численных значений производных, полученных по наблюдениям величины Y.

Вычисленные производные содержат два основных вида ошибок: вводимые при использовании численной схемы и случайные
ошибки, связанные с наблюдениями.

Исследуем численную оценку. Численное дифференцирование детерминирова-нных переменных предусматривает вычисление dy/dt или
высших производных при некотором произвольном значении независимой переменной t (напри-мер, t ₀) по заданному ряду значений у в
некотором интервале вблизи t ₀. Детерминированная ошибка в производной становится меньше, если данные концентрируются около значения t ₀, расположенного в середине интервала изменения t, чем когда значение t ₀попадает на тот или другой конец интервала. Вместо
непрерывной производной можно использовать любой из интерполяционных многочленов (Лагранжа, Грама).

Большинство схем аппроксимации для производных можно записать в общей форме

)

где а_i— постоянные;

D — дифференциальный оператор;

k — порядок производной;

h — фиксированное приращение независимой переменной;

(m +1) — число используемых опорных точек.

Следовательно, дисперсию производной можно оценить с по-
мощью формулы переноса ошибок, предполагая, что величины Y,
стохастически не зависимы, (но это практически маловероятно)

.

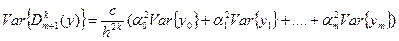Если принять дисперсии всех величин у_i, равными друг другу, то

.

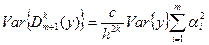Отсюда видно, что чем меньше интервал h и чем больше членов в формуле, тем больше ошибка в производной. Эта ошибка
растет с увеличением порядка производной.

Пример. В табл. 12.4 представлены численные ошибки для не-
скольких разностных формул, использованных для вычисления температурного градиента в стенке (dТ/dz)z ₀по измеренным значениям
температуры, которая считалась детерминированной переменной.

Таблица 12.4

Дата добавления: 2015-04-24