Балансовые модели

Лекция 14.

Национальное хозяйство развивается в сложной сети межотраслевых взаимосвязей, понять которые во всей их совокупности путем простого суммирования невозможно. Например, спрос на металл оказывает влияние на добычу железной руды и руд, содержащих различные металлы и вещества, необходимые для получения
стали и сплавов. Это в свою очередь увеличивает спрос на горнорудную технику. Обычные методы счета не пригодны для количественного анализа прямого и косвенного эффектов распространения таких влияний одной отрасли на другую. Решить проблему
можно только с помощью современных методов анализа, в основе
которых заложен метод межотраслевого баланса («затраты — вы-
пуск»). Этот метод разработан В. Леонтьевым. Он позволяет дать
последовательные и численно определенные ответы на вопросы, связанные с межотраслевыми взаимодействиями и их влиянием на современные макроэкономические показатели. Метод межотраслевого
баланса оказался пригоден для решения целого класса экологических задач, связанных с расходами и пополнениями экологических
ресурсов.

Рассмотрим математическую модель рационального использования природных ресурсов в процессе промышленного производства, в
котором используется модель межотраслевого баланса.

Сферу жизнедеятельности человека составляют семь основных
экологических подсистем: космос, солнечная энергия, атмосфера,
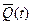почва, леса, вода, недра Земли, каждая из которых характеризуются определенными параметрами , запасами ресурсов , их
расходом 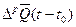за период от t₀ до t и восполнением 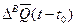за
этот же период.

Введём понятие «экологическое равновесие» для подсистем,
которое определяется условием сохранения запаса ресурсов и их
параметрами, обеспечивающими жизнедеятельность человека и
сохранность других экологических подсистем региона, что может быть представлено в виде неравенств:

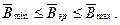
Общий запас ресурса и его параметров

.

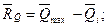
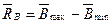Оценка запаса ресурса и его параметров в момент времени t
есть оперативный запас, который равен:

.

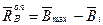В процессе жизнедеятельности за период Т человек потребляет в
среднем единиц ресурса наличное потребление и единиц
ресурса на производственные нужды. Тогда общая потребность в
ресурсах за период Т будетравна:

где N — средняя численность населения региона в период Т.

В качестве условий экологического равновесия подсистемы можно записать:

.

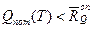при условии .

С другой стороны, желательно, чтобы расход ресурса пополнялся, т.е.:

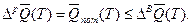
Личное потребление всех видов ресурсов за время T.

,

где n — число видов ресурсов в личном потреблении.

Потребление за единицу времени

.

При приращении личного потребления i-го ресурса на величину
за время ∆ t, предельный расход по каждому из и ресурсов
будет равен:

,

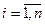т.е. скорости расхода i-го ресурса V_i.

Соответственно, для расхода ресурсов на производственные нужды:

;

;

,

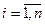
Изменение параметра b_j (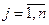) i- го ресурса (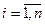) при личном

потреблении за время Т равно 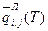за единицу времени —
Суммарное потребление по параметрам i-го ресурса

.

Суммарное потребление по параметрам всех видов ресурсов

В качестве условий экологического равновесия подсистемы можно записать:

.

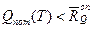при условии .

С другой стороны, желательно, чтобы расход ресурса пополнялся, т.е.:

.

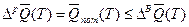Личное потребление всех видов ресурсов за время Т:

q (Т)=q,""(Т)+ц,"(Т)+...+q„(T),

где n — число видов ресурсов в личном потреблении.

Потребление за единицу времени

При приращении личного потребления i-го ресурса на величину
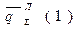за время ∆ t, предельный расход по каждому из и ресурсов
будет равен:

, i= .

т.е. скорости расхода i-го ресурса V_i,

Соответственно, для расхода ресурсов на производственные нужды:

;

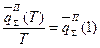
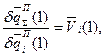i= .

Изменение параметра b _j (j' = ) i-го ресурса (i = ) при личном потреблении за время Т равно 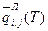за единицу времени —
Суммарное потребление по параметрам i-го ресурса –

.

Суммарное потребление по параметрам всех видов ресурсов

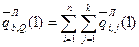. (5.35)

Функция личного потребления ресурсов

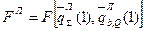, (5.36)

характеризует влияние личности на потребление ресурсов и изменение их параметров в процессе жизнедеятельности.

При потреблении ресурсов для производственных нужд по
параметрам, аналогично формулам (5.35) и (5.36), запишем

.

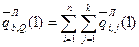Производственная функция

характеризует влияние производственной (и иной подобной деятельности) на потребление ресурсов и изменение их параметров
в процессе производства.

Таким образом, потребление ресурсов можно представить в
виде матриц:

а) суммарного потребления ресурсов:

на личное потребление

, i= .;

производственное потребление

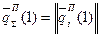
i= .

б) суммарное потребление ресурсов по параметрам:

личное потребление

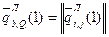, i= , i= .

производственное потребление

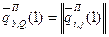i= , i= .

Общее потребление ресурсов в единицу времени

,

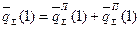Общая функция потребления

характеризует влияние личной и производственной деятельности на
экологическую систему в целом на данном этапе существования
региона (общества, проживающего в данном регионе).

Экономический механизм использования природных ресурсов
из условия «экологического равновесия» может быть представлен в
виде условий для периода времени Т (от t ₁до t ₂).

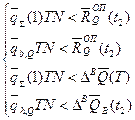
при условии

,

где — запас ресурсов кконцу периода Т;

— восстановление параметров ресурсов кконцу периода Т.

Из условия максимального уровня жизни на данный период функция полезности

.

Стоимость единицы ресурса при потреблении обозначим 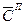по параметру b_i – 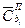. Стоимость единицы ресурса при восстановлении
(пополнении) – 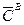; по параметру b _i — 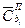. Стоимость расхода ресурсов есть функция запаса ресурсов

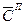= f(R _Q),

изменяющаяся в зависимости от исчерпываемости и восстанавливаемости запасов. Графики функций представлены на рис. 14.12. Отсюда видно,
что стоимость ресурса возрастает с убыванием его запаса.

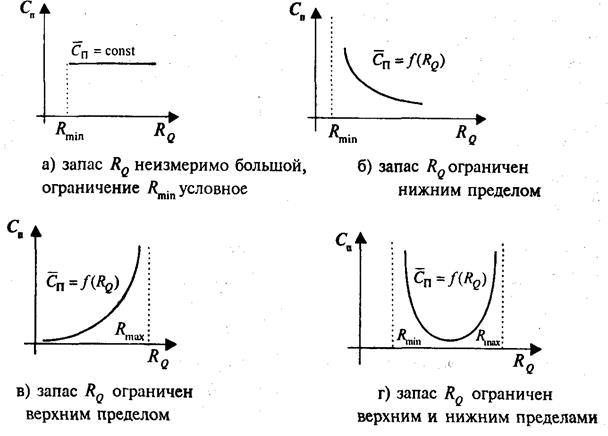
Рис. 14.12. Графики стоимости ресурсов в зависимости от их запасов

Стоимость восстановления ресурсов зависит от капитальных зат-
рат (К^в) и затрат труда (L^B), т.е.

,

а также от выбора технологий восстановления, при условии

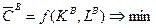
С точки зрения общественной целесообразности желательно,
чтобы цены 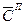и 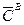были минимальны, а цена 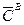, кроме того,
была бы не настолько велика, чтобы можно было организовать воспроизводство ресурса.

Следует учесть, что при восстановлении i- гo
ресурса часто требуется затратить часть других видов ресурса, в свою
очередь требующих восстановления. Если в регионе имеется k видов ресурсов (j = ) и n производственных потребителей этих ресурсов (i = ), то расход зависит от
объема выпускаемой продукции каждым из этих потребителей.

Пусть общий объем выпускаемой продукции первым предприятием , складывается из продукции, удовлетворяющей спрос других производителей, у которых она используется для производства
собственной продукции и продукции конечного спроса, поступаю-
щей на рынок, т.е.

, i= ,

где – объем выпускаемой продукции первым предприятием, который
потребляется i-ым предприятием для выпуска своей продукции.
Тогда общий объем выпускаемой продукции в регионе равен:

или в матричной форме, с учетом матрицы коэффициентов прямых затрат А с элементами:

, ,

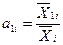и мультипликатора Леонтьева В = (1 — А)^-1, объем выпускаемой продукции по региону составит

Х = (l — А)^-1 F,

или

Х= ВF.

где l — единичная матрица размером пп;

В — матрица коэффициентов полных затрат при выпуске продукции.
Пусть каждый i -й потребитель использует i -й ресурс в количестве q_il на единицу выпускаемой продукции. Матрица удельных расходов будет иметь вид:

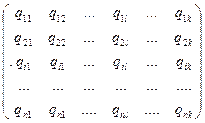
тогда расход ресурсов по региону равен:

Q= X ^TxG=(X₁, X₁, …., X₁)x 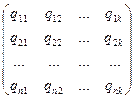=(Q₁, Q₂, …., Q_n),

где Q_i — общий расход i -го ресурса по региону l = .

При стоимости единицы ресурса с ₁, с ₂ ,..., с_l,..., с_k общая стои-
мость потребляемых ресурсов будет равна:

, или .

Обозначим общий объем l -го ресурса в регионе через R₁, а до-
пустимый расход ресурса — 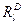. В случае, если

,

то стоимость единицы ресурса остается постоянной. Если имеет место дефицит ресурса, т.е. когда

или (5.37)

стоимость ресурса возрастает с ростом дефицита .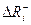

Допустим, что «экологическое равновесие» в регионе определяется условием

Q≤R^D

В этом случае основная задача экологической системы состоит
в контроле условия (5.32), которое для каждого ресурса можно за-
писать в виде

,

где — запас l -го ресурса.

В случае дефицита l -ro ресурса требуется уменьшение объема
выпускаемой продукции, для которой необходим этот ресурс. Та-
ким образом, задача становится задачей выбора решения: либо работать с дефицитом природного ресурса, либо уменьшить объём
выпускаемой продукции. В более общем виде эта задача сводится
к минимизации потерь региона, которую мы и рассмотрим.

Пусть система имеет начальное состояние S₀ удовлетворяющее по всем видам ресурсов условиям «экологического равновесия» 5.32. Из состояния S₀ система может переходить в состояния
S₁, S₂,..., S_n, каждое из которых характеризуется дефицитом при-
родных ресурсов и соответствующими объемами производства.

Если система находится в состоянии S_i, то мы имеем множество
D (S)различных допустимых решений о минимизации в этом состоя-
нии. Ожидаемые экономические потери, обусловленные решением
d D (S), в состоянии системы S_i. обозначим через R (S_i, d_i)

После того как принято решение d_i из множества возможных
D(S_i), система переходит из состояния S_i, в состояние S_i+1. Вероятность перехода из S_i в S_i+1, равна p(S_i→S_i+1, d_i). Экономические
потери от нового состояния R(S_i→S_i+1, d_i). Тогда ожидаемые потери от дефицита ресурсов 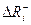и увеличения объема выпускаемой
продукции ∆ Х будут определяться условиями

назад

Дата добавления: 2015-04-24