Использование информационных технологий для решения задач экологии. 1 страница

Лекция 17.

Исследование и использование природных ресурсов, рациональное ведение хозяйственной деятельности, охрана природы и мониторинг, принятие важных практических решений, связанных с окружающей средой, невозможны без прочного информационного
обеспечения. Поэтому создание географических информационных
систем (ТИС) — одна из актуальных задач, решением которой в
настоящее время занимаются многие научные и производственные
организации.

Географическая информационная система представляет собой
совокупность технологических средств, информационных ресурсов
и персонала, позволяющих на единой географической основе поддерживать в оперативном состоянии информационную модель территории, моделировать протекающие региональные процессы и решать задачи регионального управления.

Разработка ГИС — это та сфера научно-технического прогресса,
развитие которой невозможно без опоры на картографирование и
аэрокосмическое зондирование.

Пространственные географические данные — весьма ценный
информационный продукт. Кто ими владеет, тот владеет ситуацией
и имеет шансы избежать ошибок при принятии политических, экономических, экологических решений, улаживании конфликтов,
реализации долгосрочных проектов и программ.

Источники пространственной информации многочисленны и
различны по качеству и точности. Это карты, аэро- и космические снимки, материалы статистической отчетности и кадастры (регистры), данные гидрометеорологических наблюдений, экологического
мониторинга и т.д. Сбор, хранение, увязку и обработку всех этих
данных в цифровой компьютерной форме осуществляют географические информационные системы. Они и выдают информацию пользователю по запросу в наиболее удобной для него форме — обычно, в
виде карт, схем, таблиц.

ГИС носит межотраслевой характер и призвана обеспечивать
широкий круг задач регионального управления:

• задачи учета, регистрации и оценки природного и экономического потенциала территории;

• задачи мониторинга и моделирования экономической и социальной обстановки;

• задачи комплексного развития территории, размещения производительных сил;

• обеспечение экологической безопасности и охраны природы.

Технологии в системе ГИС используются практически во всех
сферах хозяйства страны и незаменимы в случаях, где требуются
пространственно-координатные данные объекта или данные для построения информационной модели территории.

Модель формируется послойно, где каждый информационный слой объединяет группу объектов одного типа (например,
леса, реки, озера, здания, сооружения и т.п.). Однотипные объекты описаны словами, цифрами, формулами и формируют так
называемые атрибутивные данные слоя.

Принципиальным моментом является то, что создаваемые и
существующие информационные слои привязываются к единой
пространственной основе, т.е. формируются в рамках единой картографической системы.

Отличительной особенностью начального этапа развития технического обеспечения ГИС является ориентация на территориальные
вычислительные комплексы. Необходимо найти возможности для интеграции в них, что предполагает методическое и информационно--
программное единство методов и моделей реализации однотипных функций управления на различных уровнях системы.

При этом при разработке эколого-математических моделей
должно быть обеспечено согласование системы критериев и ограничений, а также единство методов, средств агрегирования и
дезагрегирования необходимой информации.

В современных условиях создание ГИС реализуется на новых
принципах в виде межведомственного территориально-распределительного вычислительного комплекса коллективного пользования (МТВК).

Основные цели создания МТВК:

• оперативность и качество обслуживания пользователей за счет
децентрализованных методов обработки данных, использования на
всех уровнях управления локальных вычислительных устройств для
первичной обработки экологической информации в местах ее возникновения;

• повышение эффективности использования вычислительной
техники за счет концентрации вычислительных ресурсов в центрах обработки данных, возможности оперативного распределения и перераспределения свободных вычислительных мощностей,
специализации отдельных вычислительных центров по сопровождению (эксплуатации) проблемно-ориентированных функциональных
программных комплексов, унификации технологии обработки данных;

• оперативность решения межведомственных задач управления
и информационного обслуживания пользователей за счет комплексирования средств вычислительной техники различных предприятий и организаций.

Требования адекватности построения генеральной схемы управления ГИС определяют выделение следующих уровней организации комплекса:

• вычислительную сеть для обслуживания экологических организаций;

• ведомственную (отраслевую) вычислительную сеть;
• межведомственную вычислительную сеть.

Взаимодействие между уровнями связано с обменом информацией при решении функциональных задач ГИС и осуществляется на уровне обмена информацией через внешние носители и
по выделенным каналам связи. При этом технология взаимодействия определяется системой территориальных стандартов.

В системе ГИС в качестве оконечных вычислительных устройств целесообразно использовать проблемно-ориентированные
автоматизированные места (АРМ).

Одной из подсистем ГИС должна быть экспертная система, как
часть искусственного интеллекта. Она включает базу данных с на-
бором правил и механизмом вывода, позволяющим на основе представляемых фактов распознать экологическую ситуацию, поставить
диагноз, формулировать решения или дать рекомендации персоналу
для выбора плана действий.

Экспертные системы (ЭС) предназначены для воссоздания опыта,
знаний профессионалов высокого уровня и использования этих знаний при управлении экологическими процессами.

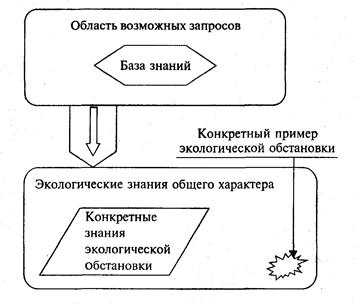
В общем виде ЭС содержат двумерный массив: область запросов и базу знаний (рис. 17.5).

Рис. 17.5. Схема базы данных и область запросов.

Область запросов — основной элемент ЭС. Если в область запросов попали какие-то данные, то систему можно запросить об этом.

База знаний содержит все знания ЭС по данному вопросу. Если
запрос соответствует конкретным знаниям экологической обстановки ЭС, то ответ может быть получен немедленно.

Если вопрос касается конкретного примера экологической
обстановки (рис. 6.5) с элементами экологических знаний обще-
го характера, то ЭС вступает в диалог с пользователем до тех
пор, пока не уточнит детали обстановки. После этого ЭС может
выдать то или иное решение по данному вопросу.

ЭСмогут быть более сложными, чем те, которые были рассмотрены. Например, машинно-обучающие экспертные системы.

назад

Специальные приложения.

Приложение 1

Значение функции

u	F(u)	u	F(u)	u	F(u)	u	F(u)
-0,00	0,5000	-0,90	0,1841	0.00	0,5000	1,80	0,9641
-0,02	0,4920	-1,00	0,1587	0,02	0,5080	2,00	0,9772
-0,04	0,4840	-1,20	0,1151	0,04		2,20	0,9861
-0,06	0,4761	-1,40	0,0808	0,06	0,5239	2,30	0,9893
-0,08	0,4681	-1,60	0,0548	0,08	0,5319	2,40	0,9918
-0,10	0,4602	-1,80	0,0359	0,10	0,5398	2,50	0,9938
-0,14	0,4443	-2,00	0,0228	0,14	0,5557	2,60	0,9953
-0,18	0,4286	-2,20	0,0139	0,18	0,5714	2,70	0,9965
-0,20	0,4207	-2,40	0,0082	0,20	0,5793	2,80	0,9974
-0,25	0,4013	-2,60	0,0047	0,25	0,5987	2,90	0,9981
-0,30	0,3821	-2,80	0,0026	0,30	0,6179	3,00	0,9986
-0,35	0,3632	-3,00	0,0014	0,35	0,6368	3,10	0,9990
-0,40	0,3446	-3,20	0,0007	0,40	0,6554	3,20	0,9993
-0,45	0,3264	-3,40	0,0003	0,45	0,6736	3,30	0,9995
-0,50	0,3085	-3,40	0,0002	0,50	0,6915	3,40	0,9997
-0,55	0,2912	-3,60	0,0001	0,60	0,7257	3,50	0,9998
-0,60	0,2743	-3,80	0,0000	0,70	0,7580	3,60	0,9998
-0,70	0,2420	-3,90		0,80	0,7881	3,70	0,9999
-0,80	0,2119	-3,9		1,00	0,8413	3,80	0,9999
				1,20	0,8849	3,90	1,0000
				1,40	0,9192	>3,9
				1,60	0,9452

Приложение 2

Значение двухстороннего критерия

Стьюдента — t_α. _k при разных уровнях значимости

Число степеней свободы к	Уровни значимости
0,10	0,05	0,01	0,001
	6,318	12,706	63,657	637,0
	2,920	4,302	9,924	31,6
	2,353	3,182	5,840	12,9
	2,132	2,776	4,604	8,610
	2,015	2,571	4,032	6,859
	1,943	2,447	3,707	5,959
	1,895	2,365	3,499	5,405
	1,860	2,306	3,355	5,041
	1,833	2,262	3,250	4,781
	1,812	2,228	3,169	4,587
	1,796	2,201	3,106	4,487
	1,782	2,179	3,005	4,318
	1,761	2,145	2,977	4,140
	1,746	2,120	2,921	4,015
	1,734	2,103	2,878	3,922
	1,725	2,086	2,845	3,850
	1,708	2,060	2,787	3,725
	1,697	2,042	2,750	3,646
	1,689	2,030	2,724	3,591
	1,684	2,021	2,704	3,551
	1,679	2,014	2,689	3,522
	1,671	2,000	2,666	3,460
	1,664		2,639	3,416
	1,660		2,626	3,391
	1,660		2,620	3,370
∞	1,645		2,576	3,291

Приложение 3

Значение критических точек критерия Пирсона

χ ² (хи-квадрат) при разных уровнях значимости

Число степе- ней свобо- ды к	Уровни значимости
0,01	0,025	0,05	0,10	0,95	0,975	0,99
	6,63	5,02	3,84	2,71	0,039	0,00098	0,00016
	9,21	7,38	5,99	4,61	0,103	0,051	0,020
	11,34	9,35	7,81	6,25	0,352	0,216	0,115
	13,28	11,14	9,49	7,78	0,71	0,48	0,29
	15,09	12,83	11,07	9,24	1,15	0,83	0,55
	16,81	14,45	12,59	10,64	1,64	1,24	0,87
	18,48	16,01	14,07	12,02	2,17	1,69	1,24
	20,09	17,53	15,51	13,36	2,73	2,18	1,65
	21,67	19,02	16,62	14,68	3,33	2,70	2,09
	23,21	20,48	18,31	15,99	3,94	3,25	2,56
	24,72	21,92	19,68	17,28	4,57	3,88	3,05
	26,22	23,34	21,03	18,55	5,23	4,40	3,57
	29,14	26,12	23,68	21,06	6,57	5,63	4,66
	32,00	28,85	26,30	23,54	7,96	6,91	5,81
	34,81	31,53	28,87	25,99	9,39	8,23	7,01
	37,57	34,17	31,41	28,41	10,90	9,59	8,26
	40,29	36,78	33,92	30,81	12,3	11,0	9,54
	42,98	39,36	36,42	33,20	13,8	12,4	10,9
	45,64	41,92	38,89	35,56	15,4	13,8	12,2
	48,28	44,46	41,34	37,92	16,9	15,3	13,6
	50,89	46,98	43,77	40,26	18,5	16,8	15,0
	63,69	59,34	55,76	51,80
	76,15	71,42	67,50	63,17
	88,38	83,3	79,08	74,40
	100,42	95,03	90,53	85,53
	112,12	106,63	101,88	96,58
	124,12	118,14	113,14	107,561
	135,81	129,56	124,34	118,50

Приложение 4

Значение функции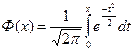

x	Ф(х)	x	Ф(х)	x	Ф(х)
0,00	0,0000	1,30	0,4032	2,60	0,4 953 380
0,05	0,0199	1,35	0,4115	2,65	0,4 959 754
0,10	0,0398	1,40	0,4192	2,70	0,4 965 330
0,15	0,0596	1,45	0,4265	2,75	0,4 970 202
0,20	0,0793	1,50	0,4332	2,80	0,4 974 449
0,25	0,0987	1,55	0,4394	2,85	0,4 978 140
0,30	0,1179	1,60	0,4452	2,90	0,4 981 342
0,35	0,1368	1,65	0,4505	2,95	0,4 984 11
0,40	0,1554	1,70	0,4554	3,00	0,4 986 501
0,45	0,1736	1,75	0,4599	3,10	0,4 990 324
0,50	0,1915	1,80	0,4641	3,20	0,4 993 129
0,55	0,2088	1,85	0,4678	3,30	0,4 995 166
0,60	0,2257	1,90	0,4713	3,40	0,4 996 631
0,65	0,2422	1,95	0,4744	3,50	0,4 997 674
0,70	0,2580	2,00	0,4772	3,60	0,4 998 409
0,75	0,2734	2,05	0,4798	3,70	0,4 998 922
0,80	0,2881	2,10	0,4821	3,80	0,4 999 276
0,85	0,3023	2,15	0,4842	3,90	0,4 999 519
0,90	0,3159	2,20	0,4860	4,00	0,4 999 683
0,95	0,3289	2,25	0,4877	4,20	0,4 999 867
1,00	0,3413	2,30	0,4892	4,40	0,4 999 946
1,05	0,3531	2,35	0,4906	4,50	0,4 999 966
1,10	0,3643	2,40	0,4918	4,60	0,4 999 979
1,15	0,3749	2,45	0,4928	4,80	0,4 999 992
1,20	0,3849	2,50	0,4937	5,00	0,4 999 997
1,25	0,3944	2,55	0,4946	-	-

Приложение 5

Значение функции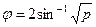

Выборочная доля Р, %	φ	Р	φ	Р	φ
0,01	0,0200		0,7079		2,3186
0,02	0,0283		0,7670		2,3746
0,03	0,0346		0,8230		2,4341
0,04	0,0400		0,8763		2,4981
0,05	0,0448		0,9273		2,5681
0,06	0,0490		0,9764		2,6467
0,07	0,0529		1,0240		2,7389
0,08	0,0566		1,0701		2,8578
0,09	0,0600		1,1152		2,9412
0,1	0,0632		1,1593	99,1	2,9515
	0,0895		1,2025	99,2	2,9741
0,3	0,1096		1,2451	99,3	2,9741
	0,1266		1,2870	99,4	2,9865
	0,1415		1,3284	99,5	3,0000
0,6	0,1551		1,3294	99,6	3,0150
0,7	0,1676		1,4101	99,7	3,0320
0,8	0,1791		1,4505	99,8	3,0521
0,9	0,1900		1,4907	99,90	3,0783
	0,2003		1,5308	99,91	3,0847
	0,2838		1,5708	99,92	3,0910
	0,3482		1,6509	99,93	3,0973
	0,4027		1,6911	99,94	3,1036
	0,4510		1,7722	99,95	3,1099
	0,4949		1,8546	99,96	3,1163
	0,5355		1,8965	99,97	3,1226
	0,5735		1,9823	99,98	3,1289
	0,6094		2,0715	99,99	3,1353
	0,6435		2,1177		3,1459
			2,2143	-	-
			2,2653	-	-

Приложение 6,а

Значение критерия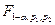

при (1-α) = 0,95 (числитель) и (1-α) = 0,99 (знаменатель)

P2	Р,
	40,52	200 4999		225 5625	234 5859	239 5981	242 6056	244 6106	248 6208	252 6302	253 6334
	18,51 98,49	19,00 99,01	19,16 99,17	19,25 99,25	19,33 93,33	19,37 99,36	19,39 99,40	19,41 99,45	19,44 99,45	19,47 99,48	19,49 99,49
	10,13 34,12	9,55 30,81	9,28 29,46	9,12 28,71	8,94 27,91	8,84 27,49	8,78 27,23	8,74 27,05	8,66 26,69	8,58 26,35	8,56 26,23
	7,71 21,20	6,94 18,00	6,59 16,69	6,39 15,98	6,16 15,21	6,04 14,80	5,96 14,54	5,91 14,37	5,80 14,02	5,70 13,69	5,66 13,57
	6,61 16,26	5,79 13,27	5,41 12,06	5,19 11,39	4,95 10,67	4,82 10,-27	4,74 10,05	4,68 9,89	4,56 9,55	4,44 9,24	4,40 9,13
	5,99 13,74	5,14 10,92	4,76 9,78	4,53 9,15	4,28 8,47	4,15 8,10	4,06 7,87	4,00 7,72	3,87 7,39	3,75 7,09	3,71 6,99
	5,32 11,26	4,46 8,65	4,07 7,59	3,84 7,01	3,58 6,37	3,44 6,03	3,34 5,82	3,28 5,67	3,15 5,36	3,03 5,06	2,98 4,96
	4,96 1,04	4,10 7,56	3,71 6,55	3,48 5,99	3,22 5,39	3,07 5,06	2,97 4,85	2,91 4,71	2,77 4,41	2,64 4,12	2,59 4,01
	4,75 9,33	3,88 6,93	3,49 5,95	3,26 5,41	3,00 4,82	2,85 4,50	2,76 4,30	2,69 4,16	2,54 3,86	2,40 3,56	2,35 3,46
	4,35 8,10	3,49 5,85	3,10 4,94	2,87 4,43	2,60 3,87	2,45 3,56	2,35 337	2,28 3,23	2,12 2,94	1,96 2,63	1,90 2,53
	4,17 7,56	3,32 5,39	2,92 4,51	2,69 4,02	2,42 3,47	2,27 3,17	2,16 2,98	2,09 2,84	1,93 2,55	1,76 2,24	1,69 2,13
	4,03 7,17	3,18 5,06	2,79 4,20	2,56 3,72	2,29 3,18	2,13 2,88	2,02 2,70	5,95 2,56	1,78 2,36	1,60 1,94	1,52 1,82
	3,89 6,90	3,09 4,82	2,70 3,98	2,46 3,51	2,19 2,99	2,03 2,69	1,92 2,51	1,85 2,36	1,68 2,06	1,48 1,73	1,39 1,59
	3,89 6,76	3,04 4,71	2,65 3,88	2,41 3,41	2,14 2,90	1,98 2,60	1,67 2,41	1,80 2,28	1,62 1,97	1,42 1,62	1,32 1,48
	3,85 6,66	3,00 4,62	2,81 3,80	2,38 3,34	2,10 2,82	1,95 2,53	1,84 2,34	1,76 2,20	1,58 1,89	1,36 1,54	1,26 1,38

Приложение 6, б

Дата добавления: 2015-04-24