Первая теорема подобия

У явлений, подобных в том или ином смысле (физически или математически), можно найти определенные сочетания параметров, называемые критериями подобия, которые имеют одинаковые значения.

Рассмотрим два процесса, описываемых однородными уравнениями.

Для первого процесса

Q ₁ + Q ₂ +……+ Q_n = 0. (2.3)

Для второго процесса

q ₁+ q ₂+ …… + q _n= 0.4)

где

Q _i= f_i(P₁,P₂,….,P_m), i = 1…. n (2.5)

q _i= f_i(R₁,R₂,…..,R_m), i = 1…. n

В уравнениях (2.3) и (2.4) Q_i и q_i - однородные функции. В свою очередь P ₁ и R ₁, Р ₂ и R ₂... P_m и R_m – сходственные переменные и параметры двух процессов. Поскольку Q_n и q_n не равны нулю, то уравнения (2.3) и (2.4) можно переписать в виде:

(2.3а)

(2.4а)

Для подобных процессов уравнения (2.3а) и (2.4а) совпадают, т.е. они тождественны. Поскольку процессы подобны, то:

; ; ……;

или

P₁ = m₁R₁; P₂ = m₂R₂; ……; P_m = m_mR_m (2.6)

После подстановки в уравнение (2.5) соотношений (2.6) вследствие однородности функции i Q можно вынести масштабы m₁,m₂, ….., m_m в соответствующих степенях за знак функции в виде общего множителя N_i, т. е.

Q_i = f_i (P₁,…..,P_m)= f_i (m₁ R₁,….., m_mR m)= N_i f_i (R₁,…..,R_m)= N_iq_i

Поскольку

Q_i = N_i q_i

то имеют место равенства

Q₁ = N₁ q₁ Q₂ = N₂ q₂ Q₃ = N₃ q₃ ……….. Q_n = N_n q_n  

(2.7)

Теперь подставим равенства (2.7) в уравнение (2.3а)

В соответствии с уравнением Фурье

N₁ = N₂ =…..= N_n

т.е.

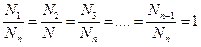
В результате от уравнения (2.3а) приходим к уравнению (2.4а).

Следовательно, уравнения (2.3а) и (2.4а) оказываются тождественными. Это означает, что между соответствующими членами уравнений (2.3а) и (2.4а) существуют соотношения:

; ; …….

Обобщая полученные результаты на S подобных процессов, получаем

где 1,2, …, S – номер процесса.

Индексы, характеризующие номер процесса, можно опустить и

записать (2.9) в общем виде

,

где idem - означает "соответственно одинаково для всех рассматриваемых процессов". Таким образом, у подобных процессов некоторые соотношения

параметров, называемые критериями подобия, оказались численно

одинаковыми. В сложных явлениях может одновременно протекать несколько различных процессов. Подобие каждого из этих процессов в отдельности обеспечивает подобие всего явления.

Обозначая критерий подобия буквой П (пи), можно дать краткую формулировку первой теоремы: для всех подобных явлений

П = idem.

Следует заметить, что справедливо и обратное положение: если критерии подобия численно одинаковы, то явления подобны. Нужно обратить внимание на практически важное свойство критериев подобия: критерии подобия любого явления могут преобразовываться в критерии другой формы, получаемые за счет операции умножения или деления ранее найденных критериев друг на друга или на какой-либо из них, т.е. если какие-либо критерии

П_k = idem и П_k+j = idem

то очевидно

П_k П_k+j = idem; ; ; k П_kj = idem.

где k - любая постоянная величина.

Заметим, что уравнение (2.3а) могло иметь совершенно иную физическую природу, чем уравнение (2.4а) при одинаковой их математической записи.

Дата добавления: 2015-04-24