Постановка задачи. Дифференциальными называются уравнения, содержащие одну или несколько производных

ЧИСЛЕННЫЕ МЕТОДЫ РЕШЕНИЯ ДИФФЕРЕНЦИАЛЬНЫХ УРАВНЕНИЙ

Дифференциальными называются уравнения, содержащие одну или несколько производных. Инженеру очень часто приходится сталкиваться с ними при разработке новых изделий или технологических процессов, так как б о льшая часть законов физики формулируется именно в виде дифференциальных равнений. Любая задача проектирования, связанная с расчетом потоков энергии или движением тел, в конечном счете, сводится к решению дифференциальных уравнений. Лишь очень немногие из них удается решить без помощи вычислительных машин. Поэтому численные методы решения дифференциальных уравнений играют такую важную роль в практике инженерных расчетов и в моделировании.

Так при реализации цифровых систем управления инженеру-системотех-нику приходится решать дифференциальные уравнения в реальном масштабе времени, т.е. непосредственно в процессе управления объектом. Примером могут служить цифровые регуляторы в системах управления электроприводами металлорежущих станков и промышленных роботов, а также цифровые системы управления автомобильными и авиационными двигателями, летательными аппаратами, морскими судами и т.д.

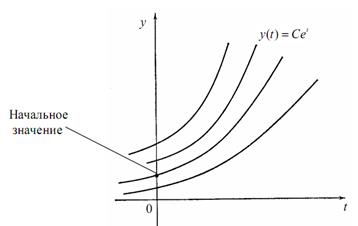
Рис. 11.3.1. Решения дифференциального уравнения

Известные математические программы – MathCAD, Matlab, Mathematica и др. непригодны для решения таких задач. Эти программы занимают в ЭВМ много памяти и, кроме того, они не могут работать в реальном масштабе времени. Поэтому для построения компактных, работающих в реальном времени цифровых моделей и систем инженеру приходится самостоятельно разрабатывать алгоритмы и программы для решения дифференциальных уравнений тем или иным численным методом.

В зависимости от числа независимых переменных и, следовательно, типа входящих в них производных дифференциальные уравнения делятся на две различные категории:

обыкновенные, содержащие одну независимую переменную и производные по ней, и уравнения в частных производных, содержащие несколько независимых переменных и производные по ним, которые называют частными.

Рассмотрим методы решения обыкновенных дифференциальных уравнений (ОДУ). Дифференциальное уравнение первого порядка можно записать в виде

y ' = f (y, t).

Это уравнение имеет семейство решений y (t). Например, если f (y, t) = y, то для произвольной константы С функция y (t) = Ce^t является решением (рис.3.1). Выбор начального значения, скажем y (0), служит для выделения одной кривой из семейства кривых. Зачастую имеется более чем одна зависимая переменная, и тогда задача заключается в решении системы уравнений первого порядка, например,

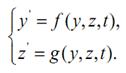
Решение этой системы содержит две постоянные интегрирования, и, следовательно, нужны два начальных условия, чтобы определить эти константы.

Если значения y и z указаны при одном и том же значении независимой переменной t ₀, то система будет иметь единственное решение. Задача определения y и z для будущих значений t > t ₀ называется задачей с начальными условиями или задачей Коши. Если же условия задаются при двух или более значениях независимой переменной, то задача называется краевой. В задаче Коши дополнительные условия называют начальными, а в краевой задаче – граничными.

Любое обыкновенное дифференциальное уравнение порядка n, которое можно записать так, что его левая часть есть производная наивысшего порядка, а в правой части эта производная не встречается, может быть записана из n уравнений первого порядка путем введения n -1 новых переменных.

Например, уравнение

u '' = g (u, u ' t)

можно записать как систему

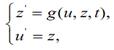
где z '(t) = u ''(t).

При обсуждении методов для задачи Коши удобно представлять

себе единственное уравнение

y '= f (y, t)

с начальным условием y (t ₀) = y₀. Однако методы с равным успехом применимы и к системам уравнений. Часто в задаче Коши в роли независимой переменной выступает время.

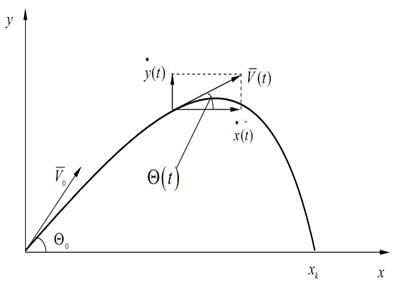
Рис 3.2. К задаче о траектории

Дата добавления: 2015-04-24