Пример 3.1

Примером может служить задача о траектории. Предположим, что снаряд выпускается с начальной скоростью V ₀ под заданным углом наклона Q₀ к поверхности.

Как видно из рис. 3.2 функции x (t) и y (t) обозначают координаты x и у снаряда в момент времени t, а функци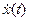и и 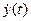определяют его скорость V (t).

Расстояние x _k, на котором упадет снаряд, зависит от целого ряда факторов: массы снаряда, начальной скорости, гравитационных сил и т.д.

Математическая модель этой задачи выводится из второго закона Ньютона:

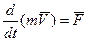(3.1)

где m - масса снаряда; F - результирующая действующих на снаряд сил.

На снаряд действуют две силы:

1) cила сопротивления воздуха

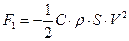(3.2)

где C - коэффициент сопротивления; ρ - плотность воздуха; S - поперечное сечение снаряда;

2) сила гравитации

F ₂= - mg, (3.3)

где g - ускорение свободного падения.

Чтобы записать уравнение (3.1) в переменных x и y, заметим, что сила сопротивления F ₁действует вдоль оси снаряда, а сила гравитации F ₂ только в вертикальном направлении. Поэтому уравнение (3.1) можно записать покоординатно следующим образом:

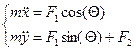(3.4)

Используя (3.2), (3.3) и меняя порядок членов, перепишем

уравнения (3.4) в виде:

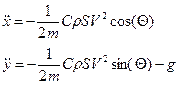(3.5)

Для численного решения необходимо преобразовать два уравнения второго порядка (3.5) в систему четырех уравнений первого порядка. Дифференцируя соотношение

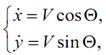(3.6)

Имеем

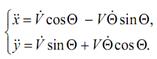(3.7)

Подставляя теперь выражения (3.7) в уравнение (3.5) и разрешая последние относительно 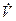и 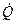, получаем

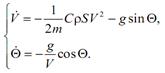(3.8)

Уравнения (3.6) вместе с (3.8) составляют систему четырех нелинейных уравнений первого порядка относительно функций x, y, V, θ. Это связанная система нелинейных дифференциальных уравнений, явное решение которых невозможно и возникает необходимость в приближенном численном решении на ЭВМ. Решение системы (3.6), (3.8) должно удовлетворять четырем необходимым начальным условиям.

Считаем, что снаряд выпускается в момент времени t = 0, так что

(x₀) = 0,

(y₀) = 0.

Другие два начальных условия даются соотношениями

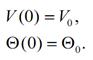
Следовательно, в данном случае рассматривается задача Коши. При заданных характеристиках снаряда и заданном V ₀ имеется только один свободный параметр – угол стрельбы Q₀. Его изменение будет, очевидно, приводить к изменению траектории.

Дата добавления: 2015-04-24