Моделировании

Применение методов подобия в математическом

Теория размерностей и подобия применяется для анализа и упрощения математических моделей. Упрощение состоит в понижении порядка системы уравнений, образующих модель, в уменьшении числа переменных или числа параметров, определяющих процесс. Системы единиц измерений можно выбирать по-разному, причем связи между величинами, определяющими модель, не должны изменяться при изменении единиц измерения.

Инвариантность явлений и процессов к изменению единиц измерения

определяется P -теоремой [11].

Пусть имеется функциональная связь

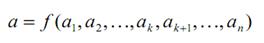(2.14)

между n +1 размерными величинами a, a ₁, …, a_n, где величины a₁, …,a_k имеют независимую размерность, и пусть эта связь не зависит от выбора системы единиц измерения (величина a определяемая, а остальные определяющие). Тогда связь (2.14) может быть записана как соотношение

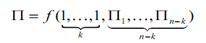(2.15)

между n +1- k критериями подобия П, П₁,…, П_n-k представляющими собой безразмерные комбинации из n +1 размерных величин а, а₁, …, а_n.

При этом критерии подобия П, П₁,…, П_n-k связаны с переменными а, а₁, …, а_nсоотношениями:

(2.16)

Здесь показатели степеней α, β, …, γ; α₁, β₁, …, γ₁; α _{n - k}, β _{n - k}, …, γ _{n - k} те

же, что и в соответствующих формулах размерностей для размерно-зависи-мых величин a, a _{K+ 1}, a_n например в формуле .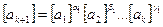

Доказательство П - теоремы основано на инвариантности связи (2.14) относительно единиц измерения.

Представим любую размерно-независимую величину a_i i = 1, …, k в виде

a_i = { a_i }[ a_i ],

где { a_i }- числовое значение величины a_i (безразмерный коэффициент); [ a_i ] - некоторая произвольно выбранная единица измерения.

Числовые значения безразмерных коэффициентов для размерно-зависимых величин a, a _{k+ 1}, a_n вычисляются с использованием выбранных единиц измерений a_i i = 1, …, k по правилу

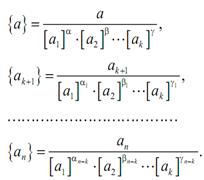
Соотношения (2.14) можно трактовать также и как связь между числовыми значениями величин a, a ₁, …, a_n (т.е. связь между безразмерными величинами { a }, { a ₁}, …., { a_n }, не зависящую, по предположению, от единиц измерения). Таким образом, для любых единиц измерений [ a_i ] справедливо равенство

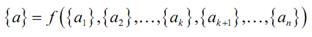
или

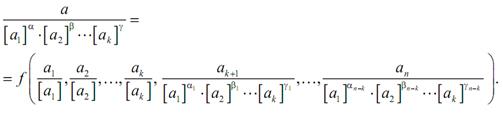
Положим теперь [ a ₁] = a ₁, [ a₂ ] = a ₂, …, [ a_k ] = a _k. Другими словами, выберем единицы измерений так, чтобы в полученной системе единиц измерений величины { a₁ }, { a₂ }, …., { a_k }тождественно равнялись единице. Тогда из последнего соотношения немедленно вытекают формулы (2.15) и (2.16).

Заметим, что поскольку единицы измерений [ a ₁], [ a₂ ], …, [ a_k ] выбраны равными самим величинам a ₁ ,a ₂, …, a _k, то эти единицы измерений не остаются постоянными. Каждым новым значениям величин a ₁ ,a ₂, …, a _kотвечают новые значения единиц измерений. Однако такой подход к выбору единиц измерений не противоречит законам теории размерностей и подобия.

Применение П -теоремы уменьшает число величин в описании объекта и позволяет явно выразить определяемую величину a, а также величины a_{k +1}, …, a _n через П, П₁, …., П_n-k и a ₁ ,a ₂, …, a _k.

В частности, если n = k, то, как следует из уравнения (2.15), П= const и

т.е. решение задачи получается в виде простого выражения через определяющие параметры. Чтобы знать точное значение a, остается определить константу.

Дата добавления: 2015-04-24