
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Пример 2.4
|
|
|
|
Пример 2.3
Определим с помощью П-теоремы критерий подобия для 2-го закона Ньютона. Этот закон можно записать как функциональную зависимость
F = f (m, l, t),
где F - сила; m - масса; l - расстояние; t - время.
Размерности параметров в классе MLT (масса, длина, время) выражаются следующими соотношениями:
[ F ] = LMT -2, [ m ] = M, [ l ] = L, [ t ] = T.
Легко видеть, что определяющие параметры m, l и t имеют независимые размерности, размерность же параметра F выражается через размерности первых трех
[ F ] = [ m ] [ l ] [ t- 2].
Таким образом, n = k = 3 и анализ размерности дает выражение для критерия подобия
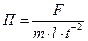 ,
,
что совпадает с результатом, который был получен для этой задачи в примере 2.1.
Определим с помощью П -теоремы критерий подобия для электрической цепи, которая была рассмотрена в примере 2.3. Цепь содержит активное сопротивление R и индуктивность L. При включении цепи на постоянное напряжение U в ней протекает процесс, который можно записать в виде функциональной зависимости
U = f (t, i, R, L).
Допустим, что определяющие параметры t, i, R имеют независимые размерности
[ t ] = T, [ i ] = I, [ R ] = L 2 MT -3 I -2.
Тогда параметры U и L будут размерно-зависимыми.
[ U ] = L 2 MT -3 I -1, [ L ] = L 2 MT -2 I -2.
В данном случае k = 3, n - k =1. Анализируя размерности параметров, находим критерии подобия.

Заметим, что в примерах 2.3 и 2.4 критерии подобия найдены на основе общих функциональных зависимостей между определяющими и определяемыми параметрами. Точные уравнения физических зависимостей нами не рассматривались. Независимость физической закономерности (2.14) от выбора
единиц измерения означает, что эту зависимость можно представить
в виде уравнения
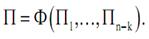
Уменьшение числа аргументов упрощает исследование. Пусть в уравнении (2.14) для выяснения зависимости величины a от некоторого определяющего параметра ai надо измерить эту величину при десяти значениях данного аргумента. Тогда для экспериментального нахождения величины a - как функции n определяющих параметров a 1 ,…, an - следует произвести 10 n экспериментов.
Согласно П - теореме, если все величины a 1, a2,…, an выражаются через k независимых размерностей, задача сводится к определению функции n - k безразмерных аргументов П1, …, П n - k, для нахождения которых достаточно 10 n - k опытов, т.е. в 10 k раз меньше. Трудоемкость установления искомой функции сокращается на столько порядков, сколько среди определяющих параметров величин с независимыми размерностями.
В примере 2.4 исходное уравнение можно заменить зависимостью
П = Ф (П1).
Следовательно, в координатах П, П1 все опытные точки должны располагаться на единой кривой. Таким образом, заранее проведенный анализ размерностей сокращает объем экспериментальной работы во много раз.
|
|
|
|
|
Дата добавления: 2015-04-24; Просмотров: 413; Нарушение авторских прав?; Мы поможем в написании вашей работы!