Види статистичної звітності в органах, які ведуть боротьбу з адміністративними правопорушеннями 10 страница

Наведемо приклад за даними табл. 19, який дасть змогу зрозумі­ти, як слід обчислювати цей показник. Візьмемо дані 1993 р. Темп зро­стання в цьому році відносно 1990 р. (базисний спосіб) становив 145,8% (539299: 369809 х 100); відносно попереднього, тобто до рівня 1992 р. (ланцюговий спосіб), — 112,2 % (539299:480478 х 100). Дані по всіх роках, наведені в стовпчиках 5 і 6 табл. 19, обчислено аналогічно.

Темп приросту характеризує, на скільки відсотків один рівень ряду більше чи менше іншого рівня. Він обчислюється як відношен­ня абсолютного приросту до рівня ряду, з яким проводиться по­рівняння. Темп приросту можна обчислити за формулами

Перша формула — це темпи приросту, обчислені ланцюговим способом; друга — базисним способом.

Темп приросту можна обчислювати й спрощеним способом — шляхом віднімання від показника темпу зростання 100 % або оди­ниці, якщо темпи зростання наведено у вигляді коефіцієнтів. Як правило, на практиці завжди використовують цей спрощений спосіб, тому що він дає змогу швидше одержати результат. У виг­ляді формули його можна записати так:

де Г — темп приросту; Г — темп зростання. Хоча темп приросту є відносною величиною, він, як і абсолют­ний приріст, може мати знак мінус. Якщо темп приросту має знак Плюс, то це свідчить про те, що явище зросло; якщо ж темп приро­сту має знак мінус, то явище зменшилося.

За даними табл. 19 пояснимо обчислення темпів приросту. Візьмемо 1995 р. і порівнюватимемо його дані з даними 1994 р. З даних, наведених у стовпчику 4, випливає, що абсолютний приріст склав 70228. Якщо застосувати перший спосіб одержання резуль­тату, то цей абсолютний приріст треба поділити на рівень 1994 р. і помножити результат ділення на 100 %, тобто (70228: 571632 х 100 %). У підсумку маємо 12, 2 %. Якщо б був застосований спрощений спосіб обчислення, то від значення, наведеного в стовпчику 6, треба відняти 100 %, і зразу одержуємо результат — 12,2 %, який і запи­сано в стовпчику 8 табл. 19.

Аналізуючи відносні величини показників інтервального ряду динаміки (темпи зростання і темпи приросту), не можна ви­користовувати їх окремо від абсолютних показників, тому що іноді уповільнення темпів зростання не супроводжується змен­шенням абсолютних приростів. Для того щоб вірно оцінити зна­чення темпів приросту, їх розглядають у порівнянні з абсолют­ним приростом, обчислюючи абсолютне значення одного відсот­ка приросту

Абсолютне значення одного відсотка приросту характеризує,

скільки одиниць досліджуваного явища знаходиться в одному відсотку його зміни. Цей показник обчислюється шляхом ділення абсолютного приросту на темп приросту за один і той же проміжок часу При цьому порівнюються лише показники, обчислені ланцю­говим способом. На практиці шляхом математичного перетворен­ня формули обчислення цього показника доведено, що абсолютне значення одного відсотка приросту дорівнює одній сотій частині базисного рівня, що він в 100 разів менше за попередній рівень ряду динаміки. Цей висновок підтверджується формулою

Останній стовпчик табл. 19 обчислено в такій спосіб. Щоб перевірити цю тезу, обчислимо, наприклад, абсолютне зна­чення одного відсотка приросту в 1992 р.: поділимо 74962 на 18,5 %. Ми одержали 4052. Але щоб обчислити темп приросту з більшим сту­пенем значущості, слід було поділити його не на 18,5 %, а 18,486 %. Якщо ми дійсно поділимо 74962 на 18,486 %, то одержимо 4055 одиниць. Отже, в 1992 р. кожний відсоток приросту складав 4055 злочинів.

Наведені дані свідчать про те, що, починаючи з 1997 р., змен­шилося абсолютне значення одного відсотка приросту відносно попереднього періоду. До цього періоду (з 1990 по 1996 р.) відбува­лось неухильне зростання даного показника.

Середній темп зростання (зниження). Після обчислення темпів зростання виникає потреба обчислити середній темп зростання, щоб охарактеризувати тенденції розвитку явища. Середній темп зростання можна обчислювати і тоді, коли ми маємо неповний ряд динаміки (лише початковий і останній рівні), де проміжні рівні відсутні. Деякі дослідники вважають, що обчислювати середній темп зростання можна лише тоді, коли явище протягом усього ана­лізованого періоду має або неухильне зростання, або зменшення. На нашу думку, це не обов'язково, тим більш, що суспільним яви­щам притаманні коливання кожного досліджуваного періоду.

Середній темп зростання характеризує, у скільки разів збільшу­вався або зменшувався рівень за певний період. Заданими табл. 19 можна обчислити середньорічний темп зростання рівня злочин­ності в Україні.

Середній темп зростання обчислюється за формулою середньої геометричної з темпів зростання, обчислених ланцюговим способом:

де т — кількість співмножників; Г/, Ту..., 7^ — темпи зростан­ня, обчислені ланцюговим способом, у коефіцієнтах.

Середній темп зростання можна обчислити з рівнів ряду, попе­редньо не обчислюючи темпи зростання. В цьому разі формула се­редньої геометричної для обчислення середнього темпу зростання матиме такий вигляд:

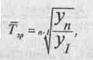
де у^ — останній член ряду динаміки; у, — перший член ряду ди­наміки.

Незалежно від того, обчислювалися темпи зростання чи ні, більш простіший і точніший результат ми одержуємо за другою формулою. Заданими, наведеними в табл. 19, обчислимо середній темп зростання злочинності в Україні за період з 1990 по 2002 р. Для цього необхідно поділити рівень 2002 р. (450661) на рівень 1990 р.

(369809) і з цієї величини здобути корінь дванадцятого ступеня (на одиницю менше, ніж рівнів ряду). В результаті цих арифметичних дій ми одержали, що середньорічний темп зростання дорівнює 101,53 %. Корінь будь-якого ступеня можна обчислювати або за допомогою спеціальних таблиць, або використовуючи відповідну обчислювальну техніку.

Середній темп приросту характеризує, як щорічно змінювався рівень ряду Реально він може мати знак плюс, що свідчить про зро­стання явища, або знак мінус, якщо явище зменшувалося. Обчис­лювати цей показник можна лише після одержання середнього тем­пу зростання: від середнього темпу зростання у відсотках відніма­ють 100 %. У загальному вигляді формулу можна записати так:

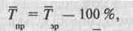
де 7д — середній темп приросту; Г — середній темп зростан­ня.

З даних табл. 19 можна зробити висновок про те, що за дослід­жуваний період злочинність в Україні в середньому зростала що­річно на 1,53 %.

§ 4. Вивчення закономірностей ряду динаміки

Одним з найважливіших завдань аналізу рядів динаміки є виявлен­ня і вивчення закономірностей у розвитку суспільних явищ і про­цесів, тобто встановлення загальної тенденції ряду динаміки та її характеру.

Під загальною тенденцією ряду динаміки (трендом) розуміють тенденцію зміни у певному напрямку рівня ряду динаміки. Загаль­на тенденція може мати вираз рівнів ряду у вигляді або сталих ве­личин, або їх неухильної зміни в бік зменшення чи зростання.

Характер ряду динаміки — це те, яким чином відбуваються ці зміни: за рівняннями прямої лінії або якоїсь кривої.

Загальну тенденцію ряду динаміки можна виявити шляхом ог­ляду рівнів ряду динаміки. Найчастіше для цього використовуєть­ся графічний спосіб.

Іноді необхідна істотна перебудова рівнів ряду. Найчастіше це відбувається тоді, коли рівні ряду внаслідок дії багатьох випадко­вих і короткочасних обставин мають коливання, які ускладнюють

аналіз показників ряду динаміки. В таких випадках у статистиці застосовують різні прийоми перебудови рядів динаміки з метою виявлення прихованих закономірностей, які неможливо виявити візуально. Головні із цих методів — укрупнення інтервалів, обчис­лення ковзної середньої, аналітичне вирівнювання.

Найпростіший метод — укрупнення інтервалів (періодів) — це перехід від первинних даних до укрупнених середніх даних за більший відрізок часу. Наприклад, якщо ми маємо первинні дані за кожний окремий місяць, то їх можна замінити на дані за квартал, півріччя або рік. Таке укрупнення інтервалів проводиться поступо­во: від малих до все більших інтервалів, поки загальна тенденція ряду динаміки не стане досить чіткою. Але слід відзначити, що за­стосування цього способу можливо лише при рівності порівнюва­них інтервалів. При такому способі кількість членів ряду динаміки значно скорочується, а також випадає з поля зору рух рівнів ряду динаміки усередині цього укрупненого періоду. Укрупнені періоди обов'язково характеризуються середніми рівнями ряду.

В табл. 20 наведено дані про кількість зареєстрованих злочинів по лінії карного розшуку для обчислення і виявлення загальної тен­денції ряду динаміки.

У стовпчику 3 табл. 20 відмічено, що вирівнювання здійснюєть­ся за квартал. У стовпчику 4 цієї ж таблиці обчислено загальну

Таблиця 20 Кількість зареєстрованих злочинів по місяцях

Місяць	Кількість злочинів	Період укрупнен­ня, квартал	Загальна кількість за період	Середня кількість за період	Ковзна середня за три місяці	Теоретична пряма. У,
січень					-	36695,12
лютий		І		37235,3	37235,3	37397,24
березень					40961,7	38099,36
квітень					41377,3	38801,48
травень		П		41073,7	41073,7	39503,6
червень					40573,3	40205,72
липень					40256,0	40907,84
серпень		Ш		40224,0	40224,0	41609,96
вересень					40254,7	42312,08
жовтень					40389,3	43014,2
листопад		IV		43694,0	43694,0	43716,32
грудень					-	44418,44

кількість зареєстрованих злочинів за квартал. Після цього обчислює­мо середню кількість зареєстрованих злочинів за кожний місяць про­тягом кварталу. Ця середня кількість обчислюється шляхом ділення загальної кількості на три місяці, тобто за середньою арифметичною простою. Дані, наведені в стовпчику 5 табл. 20, підкреслюють на­явність деякої тенденції до зростання кількості зареєстрованих зло­чинів в IV кварталі року порівняно з І кварталом цього ж року.

Значно більші можливості для аналізу ряду динаміки має зас­тосування методу ковзної середньої. Сутність цього методу полягає в тому, що кожний рівень ряду динаміки замінюється на середню величину, яка обчислюється із даного і сусідніх рядів. Цей спосіб одержав назву за техніку обчислення: кожна наступна середня ве­личина обчислюється шляхом переміщення на один рівень ряду. В нашому прикладі спочатку обчислюється середній рівень за три місяці (січень, лютий, березень), а потім — за лютий, березень і квітень і т.д.

Результати обчислення ковзної середньої обов'язково відносять до середини періоду, тому, як правило, її обчислюють з непарного числа рівнів ряду. Якщо період включатиме парну кількість рівнів ряду, то обчислені середні величини необхідно відносити до сере­дини проміжку між двома рівнями ряду.

В стовпчику 6 табл. 20 наведено ковзну середню величину, об­числену за три місяці. З цих даних видно, що наприкінці року дійсно реєструється значно більше злочинів, ніж на початку. Можна обчислити ковзну середню і за більший проміжок часу. Існує дум­ка, згідно з якою чим більший проміжок часу береться за інтервал для обчислення ковзної середньої величини, тим більш зрозумілою стає загальна тенденція ряду динаміки, але в той же час завжди ско­рочується кількість рівнів на величину: тривалість інтервалу ви­рівнювання мінус одиниця. Стовпчик 6 табл. 20 дійсно коротший на два рівні, ніж первинні дані, тому що інтервал вирівнювання дорівнює трьом (3 — 1), тобто зникають один рівень на початку ряду динаміки і один наприкінці.

До недоліків згладжування ряду динаміки методом ковзної середньої належать: 1) неможливість обчислення показників для початкових і останніх рівнів ряду; 2) довільність вибору інтерва­лу згладжування, що може істотно впливати на одержані резуль­тати. Тому цей метод використовується з метою попередньої оцінки наявності чи відсутності загальної тенденції зміни рівнів ряду динаміки.

Найбільш досконалим методом для виявлення загальної тен­денції та її характеру є аналітичне вирівнювання рядів динаміки. Ана­літичне вирівнювання — це основа для використання інших методів поглибленого вивчення рядів динаміки з метою проведення стати­стичного аналізу взаємозв'язків між явищами.

Сутність аналітичного вирівнювання — це знаходження матема­тичного вираження закономірностей (рівняння прямої лінії, гіпер­боли, параболи або якоїсь іншої). Знаходять таке рівняння, яке мак­симально наближуватиметься до первинних даних Наприклад, на графіку (рис. 17) наносимо первинні дані (табл. 20), ковзну середню і будуємо теоретичну пряму лінію, яка з точки зору математики найбільш близько підходить до первинних даних. У математиці з цією метою застосовується метод найменших квадратів, за допомо­гою якого визначають параметри аналітичного рівняння обраної лінії, тобто щоб сума квадратів відхилень фактичних рівнів від вирів­няних, які розташовані на теоретичній лінії, була б найменшою.

Технічно вирівнювання зводиться до заміни фактичних рівнів ряду такими, які б у середньому менше за все відхилялися від фак­тичних, мали певне аналітичне вираження. За даними, наведени­ми в табл. 20, побудуємо теоретичну лінію у вигляді рівняння

де 3^— теоретична лінія значень; а у а^— параметри теоретичної лінії; /— час, порядкові номери проміжків або моментів часу (абс­циси точок прямої).

Параметри ОдТао, теоретичної прямої, яку ми повинні знайти з урахуванням вимог методів найменших квадратів, знаходяться шля­хом розв'язування системи рівнянь. Розв'язавши систему рівнянь, знаходимо, що теоретична лінія матиме вигляд У= 35993 + 702,12/. Результати вирівняних рівнів, одержані внаслідок такого вирівню­вання вихідних даних, наведено в останньому стовпчику табл. 20.

Після всіх проведених розрахунків побудуємо ці дані у вигляді графіку (рис. 17):

Проведене аналітичне вирівнювання на основі прямої лінії дає змогу лише виявити основну закономірність зміни явища. З точки зору математичного аналізу можна використовувати більш складні форми зв'язку. Застосування сучасної обчислювальної техніки значно спрощує техніку обчислення, але підвищує вимоги до рівня обізнаності дослідника, який повинен мати більш чітке уявлення про наявність і форму зв'язку між явищами.

Щорічні рівні більшості суспільних, особливо правових, явищ залежать від сезонних коливань. Перебудова рівнів ряду динаміки за­стосовується для їх виявлення і обчислення індексів сезонності. Індекс сезонності — це відношення кожного рівня ряду динаміки у вигляді відсоткового відношення рівнів кожного місяця до якогось теоретичного, як правило, середнього рівня за рік, який приймається за базу порівняння. Розрахунок можна навести у вигляді формули

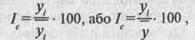
де / — індекс сезонності; у,— фактичні щомісячні рівні ряду; у, — вирівняні рівні (рівні теоретичної лінії); у — середня величина із щомісячних рівнів ряду.

Для більшої надійності одержаних результатів індекси сезон­ності обчислюються за даними за три роки (або більший проміжок

часу). В цьому випадку для кожного місяця обчислюється середня величина рівня за три роки, яка і порівнюється із загальним серед­ньомісячним рівнем за три роки, або для кожного року окремо об­числюються щомісячні індекси сезонності, з яких потім обчис­люється середній рівень для кожного місяця.

Існують й інші, більш складні методи обчислення індексів се­зонності.

Сезонні коливання властиві абсолютній більшості юридичних явищ. Тому їх аналіз має велике значення для планування заходів протидії злочинності, прийняття відповідних управлінських рішень, розв'язання питань оперативного і матеріально-технічно­го забезпечення діяльності правоохоронних органів.

§ 5. Інтерполяція, екстраполяція та прогнозування з використанням рядів динаміки

Вивчення рядів динаміки різних суспільних явищ дає базу для прогнозування і знаходження невідомих рівнів ряду.

Інтерполяція — це метод побудови рядів динаміки за попередній період, коли з якихось причин були відсутні відомості про розміри явища, або для знаходження невідомих проміжних рівнів ряду ди­наміки. Відсутність цих даних може зумовлюватися різними при­чинами: був відсутній облік цих явищ у попередній час, змінилася методика обчислення показника тощо. Для того щоб обчислити невідомі рівні ряду динаміки, проводять математичні розрахунки різної складності.

Невідомі рівні ряду динаміки знаходять або на базі сусідніх відо­мих значень ряду динаміки шляхом обчислення їх середньої ариф­метичної простої, або на базі взаємозв'язку цього явища з іншими, кількісний вираз яких відомий. При застосуванні методу інтерпо­ляції робиться припущення, що загальна тенденція, яку ми маємо зараз, мала місце і в попередній інтервал часу. При застосуванні цього методу завжди проводяться математичні розрахунки різної складності.

Наприклад, таким чином можна обчислити населення країни протягом року, оскільки офіційна статистика обов'язково наводить дані лише на початок кожного року.

Інтерполяція дає змогу приблизно відобразити ті законо­мірності, які склалися протягом певного періоду.

Екстраполяція — це метод подовження кількісних характерис­тик сукупностей за межі досліджуваного явища в майбутнє на базі встановлених закономірностей за попередній строк. За допомогою методу екстраполяції можуть бути зроблені висновки, одержані внаслідок вивчення однієї частини сукупності та поширені на її іншу аналогічну частину.

В основі використання методу екстраполяції лежить припущен­ня, що чинники, які зумовили розвиток даного явища, залишають­ся незмінними і протягом наступного періоду. Цей метод в останні роки найчастіше застосовується для прогнозування явищ лише на короткий проміжок часу.

Використовуючи метод екстраполяції, можна прогнозувати кількість населення, його міграцію, а також зміни в правових явищах.

Для екстраполяції найчастіше застосовують аналітичний метод вирівнювання ряду динаміки. Заданими, наведеними в табл. 20, мож­на спрогнозувати, чому дорівнюватиме кількість зареєстрованих зло­чинів у перший місяць наступного року Для цього у формулу У,= 35993 + 702,12/, підставимо {, яке дорівнює 13 (ми проаналізували дані за 12 місяців поточного року, тому у формулі з метою прогнозу числа зареєстрованих злочинів у січні майбутнього року приймаємо / == 13). Одержимо, що кількість їх становитиме 45 121 злочин. Коли матиме­мо первинні дані, то можна порівняти, на скільки відрізнятиметься наш рівень прогнозу від реальної кількості зареєстрованих злочинів.

Можливе і таке обчислення наступних рівнів ряду динаміки:

кінцевий рівень помножують на середній темп зростання.

Методи інтерполяції і екстраполяції в статистиці застосовують для прогнозування, планування та кореляційного аналізу розвит­ку правових явищ. Використання цих методів можливо лише тоді, коли явища змінюються стабільно. Вперше на можливість спро­гнозувати показники статистичних рядів на нетривалий період звернув увагу А.Кетле, який з великою достовірністю спрогнозував кількість вчинених злочинів у Франції в 1830 р. на базі статистич­них даних 1829 р. На цьому ґрунті пізніше виникла теорія устале­ності статистичних рядів В.Лексіса.

Тому при прогнозуванні на тривалий час ми завжди повинні використовувати методи інтерполяції і екстраполяції в сукупності з іншими методами, такими як методи експертних оцінок, матема­тичного модулювання і т. под.

Питання та завдання для самоконтролю

1. Що в статистиці називають статистичним рядом? Наведіть класифікацію статистичних рядів.

2. Дайте визначення поняття рядів динаміки. Пере­рахуйте їх види.

3. Назвіть вимоги до правильної побудови рядів ди­наміки.

4. Охарактеризуйте показники, які обчислюються в моментних рядах динаміки.

5. Охарактеризуйте показники, які обчислюються в інтервальних рядах динаміки.

6. Розкрийте основні методи перетворення рядів ди­наміки.

7. Дайте визначення понять «інтерполяція», «екст­раполяція» та «прогнозування».

Завдання 1. Обчисліть середній рівень ряду дина­міки за даними про кількість зареєстрованих злочинів у районі: 1996 р. — 101 злочин; 1997 р. — 99; 1998 р. — 101; 1999 р. - 95; 2000 р. - 103; 2001 р. - 97; 2002 р. -87. Який вид ряду динаміки наведено в цьому завданні?

Завдання 2. Маємо такі дані про кількість та рух засуджених у виправно-трудовій установі загального режиму: на 1 січня було 900 засуджених, 20 лютого прибуло ЗО засуджених, 10 березня вибуло 10 засудже­них, 25 березня прибуло 15 засуджених. Обчисліть се­редню кількість засуджених у виправно-трудовій ус­танові загального режиму протягом першого кварталу. Який вид ряду динаміки наведено в цьому завданні?

Завдання 3. Маємо такі дані про залишки нерозгля-нутих районним судом цивільних справ на початок місяця: на 1 січня — 40, на 1 лютого — 45, на 1 березня — 40, на 1 квітня — 46, на 1 травня — 49, на 1 червня — 47, на 1 липня — 52. Обчисліть середній залишок нероз-глянугих цивільних справ на перший та другий кварта­ли. Який вид ряду динаміки наведено в цьому завданні?

Завдання 4. Маємо такі дані про кількість розгля­нутих у суді житлових справ: липень — 300, серпень — 450, вересень — 420, жовтень — 400, листопад — 280, грудень — 220. Обчисліть середній рівень ряду (за півроку), абсолютний приріст (зменшення), темпи

зростання і приросту (зменшення). Який вид ряду динаміки наведено в цьому завданні?

Завдання 5. За даними завдання 1 визначте абсо­лютний приріст, темпи зростання та приросту (змен­шення) базисним способом.

Завдання 6. За даними завдання 1 обчисліть абсо­лютний приріст (зменшення), темпи зростання та приросту (зменшення) ланцюговим способом.

Завдання 7. За даними завдання 1 обчисліть абсо­лютне значення 1 % приросту (зменшення).

Індекси

§ 1. Поняття індексного методу

Слово «індекс» (іпсіех) означає «показник» і застосовується в різних галузях науки.

Індексом у статистиці називається відносний показник, який характеризує зміну рівня якогось суспільного явища з часом або його співвідношення у просторі, а також порівняно з плановим завданням.

У статистичній практиці, особливо в економічній статистиці, індекс є найбільш вживаним узагальнюючим показником. За допо­могою індексів характеризується розвиток національної економі­ки в цілому та окремих її галузей, аналізуються наслідки виробни­чо-господарської діяльності підприємств, досліджується роль ок­ремих факторів у формуванні важливіших економічних показників, виявляються резерви (особливо приховані) виробництва. Індекси використовуються також для міжнародних зіставлень економічних показників, визначення рівня життя населення і т.под.

Юристам також досить часто доводиться мати справу з індекс­ним методом при аналізі правових явищ, наприклад, при розсліду­ванні господарських, службових злочинів, аналізі висновків бухгал­терської, товарознавчої експертиз, для орієнтації у складних еко­номічних питаннях.

Широкою є амплітуда застосування індексного методу при про­веденні кримінологічних досліджень. За його допомогою можна простежити динаміку зміни тяжкості окремих видів злочинів і сту­пеня суспільної небезпечності злочинності у цілому і по окремих видах злочинів. Це дає змогу ефективніше вирішувати питання у сфері попередження злочинності та інших правопорушень.

Цими обставинами і зумовлюється необхідність знання індекс­ного методу для аналізу соціально-правових явищ.

Як відомо, більшість суспільних явищ, які вивчаються статис­тикою, складаються із багатьох окремих елементів. У практиці статистичної роботи до індексів належать показники, які характеризують не тільки співвідношення цих явиш у цілому, а й їх окремих складових частин.

У нашій країні в теорії індексів склалися два напрямки: узагаль­нюючий, або синтетичний, та аналітичний, які і обумовлюють мож­ливість інтерпретації індексів. За допомогою індексів можна виріши­ти такі основні завдання: 1) характеристика загальної зміни склад­ного економічного показника (наприклад, витрат на виготовлення або придбання продукції) або формуючих його окремих показників (факторів); 2) виділення у зміні складного показника впливу одно­го із факторів шляхом виключення впливу інших факторів (наприк­лад, зростання виторгу від реалізації під впливом зростання цін без урахування зміни виробництва продукції в натуральному виразі).

Способи побудови індексів залежать від змісту показників, що вивчаються, методології їх розрахунку, наявних вихідних даних і цілей дослідження.

За ступенем охоплення елементів сукупності прийнято розріз­няти дві категорії індексів: індивідуальні та загальні. Індекс, який характеризує співвідношення величин окремого явища, називаєть­ся індивідуальним. Він позначається літерою і та супроводжується показником індексованої величини (тієї величини, зміна якої вив­чається). Індекс, який характеризує співвідношення рівнів усього явища в цілому або його частин, що складаються з кількох окремих елементів, які безпосередньо не піддаються підсумовуванню, нази­вається загальним. Він позначається літерою /і також обов'язково супроводжується показником індексованої величини, оскільки лише в цьому разі ми можемо визначити назву загального індексу. Загальні індекси, на нашу думку, належать до узагальнюючих по­казників.

Отже, індивідуальні індекси — це відносні величини планово-і го завдання, виконання плану, динаміки (темпи зростання) і по" ^! рівняння. Решта видів відносних величин до індексів не належить. ''• Індивідуальні індекси обчислюються подібно тому, як обчислюєть­ся та чи інша відносна величина.

; Окремі елементи, з яких складається те чи інше суспільне яви- \ ще, можуть бути однорідними і неоднорідними. Однорідні елемен­ти можна підсумовувати. Особливості індексного методу, які дають змогу відрізняти його від методу обчислення відносних величин,

проявляються при розрахунку індексів для складного явища, оди­ниці якого не піддаються безпосередньому підсумовуванню, тому що вони можуть мати різні споживчі властивості (наприклад, 1 тон­на пшениці та 1 тонна сталі) або різні одиниці вимірювання (на­приклад, кількість виробленої продукції тваринництва: молока, м'яса тощо в натуральних одиницях виміру).

Безпосередня несумісність окремих частин складного явища зовсім не означає, що їх не можна взагалі зробити сумісними. У цьому разі, якщо окремі частини у розглядуваному відношенні є якісно однорідними, то для них завжди можна і треба знайти загаль­ну міру, тобто спільномірник. Інакше кажучи, для обчислення за­гальних індексів виникає потреба в застосуванні спеціальних за­собів, які становлять специфіку індексного методу.

Залежно від змісту та характеру індексованої величини розріз­няють індекси кількісних показників (наприклад, індекс кількості суддів і судів, фізичного обсягу продукції) та індекси якісних показ­ників (наприклад, індекс цін, собівартості, злочинності)

Залежно від вибору бази порівняння, яка визначається метою дослідження, існують два можливі способи розрахунку індексів:

Дата добавления: 2015-04-24