Види статистичної звітності в органах, які ведуть боротьбу з адміністративними правопорушеннями 12 страница

тиці, фізиці, астрономії тощо. Він виражається точною математич­ною формулою, яка може бути використана у будь-якому випадку для розглядуваного явища. Так, площа кола (результативна ознака) прямо пропорційна радіусу (факторній ознаці) і виражається фор­мулою 8 == п К², а зв'язок між довжиною кола і радіусом — форму­лою /= 2л" 7?. Прикладами функціональної залежності результатив­ної ознаки від декількох факторних ознак можуть бути: залежність току від напруги і опору, залежність площі трикутника від величи­ни його сторін.

Функціональна залежність проявляється з однаковою силою в усіх одиницях сукупності незалежно від зміни інших ознак даного явища. Наприклад, встановлена залежність площі кола від квадрата радіуса проявлятиметься всюди: і при обчисленні площі кола дис­ка для метання в спортивних змаганнях, і при характеристиці площі кола майдану міста чи села та ін. Отже, якщо встановлено функціо­нальну залежність на базі одиничного дослідження, то нею можна користуватися в усіх аналогічних випадках.

Функціональна залежність має місце і в суспільних явищах, але дуже рідко, і ці зв'язки є одиничними, відображають взаємозв'язок тільки окремих сторін явищ. Наприклад, таким є зв'язок тарифної заробітної плати і відпрацьованого робітником робочого часу тощо. В правових явищах функціональна залежність, як правило, не зус­трічається.

При кореляційному зв 'язку між причиною і наслідком не має повної відповідності, а спостерігається лише певне співвідношен­ня. Під впливом зміни багатьох факторних ознак (деякі з яких мо­жуть бути невідомі) змінюється середня величина результативної ознаки. Кореляційні зв'язки найбільш поширені серед суспільних явищ. Так, між рівнем злочинів проти безпеки виробництва і по­рушенням вимог законодавства про охорону праці на підприєм­ствах є певна взаємозалежність, якщо мати на увазі значну кількість випадків. Але на рівень злочинності у цій сфері впливають і такі фактори, як режим роботи на підприємстві, стан техніки, особисті якості виробничого персоналу та ін.

Або візьмемо зворотну залежність між насильницькою злочинні­стю і освітою осіб, що вчинили злочини. Така залежність є, але на рівень злочинності в різних напрямках діють багато інших факторів (вживання алкоголю, моральні якості особи, матеріально-побутові умови тощо). Тому в кожному конкретному випадку залежність між

освітою і злочинністю може не проявитися і для виявлення такої не­повної залежності треба взяти велику кількість явищ, які слід розгля­дати в сукупності. Подібним чином можна вивчати і залежність між злочинністю і рецидивом, між злочинністю і питомою вагою осіб, які вчинили злочини у складі групи, по окремих видах злочинів.

У цивільно-правової статистиці можна вивчати: залежність між зростанням житлового будівництва і зниженням кількості судових справ відповідної категорії (справ, які виникали на ґрунті сімейно-побутових конфліктів), залежність між кількістю розлучень на 10 тис. населення і умовами життя населення, між кількістю укладених шлюбів на 10 тис. населення і соціально-демографічними показни­ками всього населення тощо.

Отже, наявність багатьох факторних ознак, ступінь впливу яких на результативну ознаку невідомий, є однією з характерних особ­ливостей кореляційних зв'язків. Кореляційний зв'язок між резуль­тативною ознакою і одиницею з певної кількості факторних ознак може проявитися лише в загальному, середньому, при інших одна­кових умовах. Вплив факторів, які не є об'єктом дослідження, усу­вається шляхом заміни їх на середні показники. Відповідно до за­кону великих чисел це досягається на підставі взаємопогашення відхилень ознак певних одиниць в той чи інший бік від середньої при достатньо великій кількості одиниць, що вивчаються. Чим більша статистична сукупність, тим точніше встановлюване співвідношення виражає закономірність кореляційних зв'язків.

Слід ураховувати і те, що у складних взаємовідносинах може знаходитися і результативний фактор — у більш загальному вигляді він може виступати як фактор зміни інших ознак. Це потребує того, щоб результати кореляційного аналізу мали значення для даного виду зв'язку, а інтерпретація цих результатів вимагає побудови си­стеми кореляційних зв'язків у більш загальному вигляді.

Але і на масовому статистичному матеріалі виявлені залежності не матимуть повного, функціонального характеру. Вони певною мірою наближатимуться до функціонального зв'язку, але дія інших факторів, не врахованих дослідженням, призводить до того, що кореляційний зв'язок завжди буде неповним. З цього випливає, що кореляційний зв'язок не виражається певною математичною формулою, він може бути виражений лише приблизно за допомогою аналітичних формул.

За напрямком зв'язку між явищами розрізняють зв'язки прямі та обернені. Якщо із збільшенням факторної ознаки є тенденція до

зростання індивідуальних і середніх значень результативної озна­ки, то це буде прямий зв'язок. Якщо із збільшенням факторної оз­наки результативна ознака зменшується або, навпаки, із зменшен­ням факторної ознаки результативна ознака зростає, то це є обер­нений зв'язок. Наприклад, між пияцтвом і злочинністю є пряма залежність, а між освітою і злочинністю — обернена.

За кількістю взаємодіючих факторів зв'язки можуть бути однофак-торними та багатофакторними. Однофакторні зв'язки — це такі, при яких одна результативна ознака пов'язана з однією факторною оз­накою. Такий зв'язок називають парним. Багатофакторні зв'язки — це такі, при яких одна результативна ознака пов'язана з двома або більшою кількістю факторних ознак. У суспільних явищах найчасті­ше зустрічаються багатофакторні зв'язки. Так, на рішення розірва­ти шлюб впливають багато факторів; на вчинення автотранспортного злочину впливають різні фактори: природні умови, стан дороги, стан транспортних засобів, кваліфікація водія, додержання правил дорож­нього руху водіями та іншими учасниками руху тощо.

За аналітичним вираженням розрізняють прямолінійні (лінійні) та криволінійні (нелінійні) зв'язки. При прямолінійному зв'язку із зрос­танням факторної ознаки відбувається рівномірне зростання (або зменшення) результативної ознаки. Математично такий зв'язок по­значається рівнянням прямої у^ == Од + аре, а графічно — прямою лінією. Тому такий зв'язок і називають лінійним. При криволінійно­му зв'язку із зростанням факторної ознаки зростання (або зменшен­ня) результативної ознаки відбувається нерівномірно або напрямок зв'язку змінюється з прямого на обернений. Геометричне такий зв'я­зок позначається кривими лініями (гіперболою, параболою тощо).

При цьому слід мати на увазі, що лише функціональний зв'язок аналітичним рівнянням виражається точно, а кореляційний зв'язок — лише приблизно, за умови абстрагування від впливу всіх інших ознак. Тому на графіку матиме місце розкидання точок навколо лінії.

§ 3. Прийоми виявлення щільності зв'язку між показниками досліджуваних явищ

Для вивчення кореляційної залежності, інакше кажучи, для від­повіді на питання про наявність чи відсутність кореляційного зв'яз-

ку, застосовують різні методи: балансовий, порівняння паралельних рядів, статистичних групувань, графічний, регресійного та дисперсій­ного аналізу зв'язків та інші методи математичної статистики.

Балансовий метод. Цей метод широко застосовується в статис­тиці для вивчення зв'язку і пропорцій між явищами. Сутність його полягає в тому, що дві суми абсолютних величин пов'язані між со­бою знаком рівності, наприклад:

В такий спосіб можна побудувати баланс надходження до місце­вого суду і розгляду тих чи інших категорій справ, який можна ви­користовувати в контрольних цілях.

При розслідуванні кримінальних справ про економічні злочи­ни цей прийом дає змогу проаналізувати співвідношення між над­ходженням сировини і випуском продукції, наявність і використан­ня окремих ресурсів.

Балансовий метод вивчення взаємозв'язків дуже часто застосо­вується в економічній статистиці. У правовій статистиці цей метод використовується рідко, в основному в практичній діяльності різних правоохоронних органів для побудови балансу руху кримі­нальних, цивільних або адміністративних справ.

Метод порівняння паралельних рядів. Цей метод широко застосовується для встановлення зв'язку між взаємопов'язаними явищами. Сутність його полягає в тому, що дані ряду факторної оз­наки розміщуються за принципом її зростання, або зменшення, або за якимось іншим принципом, і паралельно наводиться ряд даних результативної ознаки, яка залежить від факторної. Шляхом по­рівняння наведених рядів виявляють наявність і напрямок зміни ре­зультативної ознаки залежно від зміни факторної ознаки. У випад­ках, коли зростання факторної ознаки тягне за собою зростання і величини результативної ознаки, можна говорити про наявність пря­мої кореляційної залежності. Якщо ж із збільшенням факторної оз­наки величина результативної ознаки має тенденцію до зменшення, то можна припустити наявність оберненого зв'язку між ознаками.

Наявність великої кількості різних значень результативної оз­наки ускладнює сприйняття таких паралельних рядів, особливо за наявністю значної кількості одиниць, які становлять статистичну

сукупність. У цьому випадку для встановлення факту наявності або відсутності зв'язку доцільно використовувати групові таблиці.

Паралельні ряди можна порівнювати як в статиці, тобто за один і той же час порівняння, так і в динаміці — порівнювати дані за окре­мі хронологічні періоди. Якщо треба порівняти ряди динаміки од­нойменних показників на різних територіях, то можна порівнюва­ти не тільки абсолютні прирости і темпи зростання, а й рівні на однакові дати, щоб одержати відповідь на питання, на скільки рівень одного ряду більше або менше іншого. Можна порівнювати ряди динаміки середніх і відносних величин, що робить статистич­ний аналіз більш глибоким та всебічним.

Ряди розподілу можна використовувати для порівняння розпо­ділу всього населення і осіб, що вчинили злочини, за віком, стат­тю, соціальним, родинним станом тощо. При цьому порівнянні можна встановити, на скільки часто, за той чи інший проміжок часу зустрічається та чи інша група серед осіб, що вчинили злочини, ніж серед усього населення.

Краще порівнювати ряди динаміки, ніж ряди розподілу. При порівняльному аналізі рядів динаміки з метою наочного встанов­лення взаємозалежності між явищами доцільно привести ряди до однієї основи, до загальної бази порівняння. За загальну базу по­рівняння може бути взято не тільки який-небудь безпосередній рівень ряду, а й середній рівень. Приводити ряди динаміки до однієї основи треба тоді, коли ряди характеризують динаміку різних, без­посередньо не сумісних, але взаємопов'язаних рядів. Цей метод ви­користовується в статистичній практиці для виявлення щільності між показниками досліджуваних явищ. За допомогою цього мето­ду можна аналізувати однойменні дані, які належать до різних те­риторій, наприклад, порівнювати динаміку коефіцієнта злочин­ності в різних країнах за певний проміжок часу.

Іноді виникає питання: в яких випадках при вивченні паралель­них рядів можна порівнювати їх рівні відносно базисного (почат­кового) рівня, а в яких — середнього рівня? У загальній теорії ста­тистики існує така точка зору: якщо ряд динаміки має сталу тенден­цію до зростання або зменшення, то лише тоді його треба порівнювати відносно базисного рівня. У правовій статистиці кра­ще порівнювати рівні паралельних рядів відносно базисного рівня без урахування тенденцій зміни того чи іншого явища.

Цей метод вивчення взаємозв'язків між явищами може засто­совуватися і у правовій статистиці. Можна, наприклад, порівнюва-

ти ряди про кількість засуджених за хуліганство і про кількість спо­житого алкоголю на 100 тис. населення по окремих районах, містах або за окремі роки; кількість вчинених злочинів, кількість осіб, що вчинили злочини, і кількість засуджених. У цивільно-правовій ста­тистиці можна порівнювати ряди кількості побудованого житла та інтенсивності житлових спорів (на 10 тис. населення); кількості за­реєстрованих шлюбів і розлучень на 10 тис. населення по окремих районах або за окремі періоди тощо.

Проаналізуємо за допомогою паралельних рядів, чи стають більш молодими злочинці в районі міста за декілька років. Моло­дими у кримінально-правовій статистиці вважаються особи до ЗО років (табл.22).

Таблиця 22 Дані про кількість зареєстрованих у районі міста злочинів

Рік
Кількість осіб, що вчинили злочини
У віці до ЗО років
Питома вага у віці до ЗО років	52,1	49,4	52,2	57,4	58,9

Абсолютні і відносні дані, наведені в табл. 22, не дають змоги встановити наявність чи відсутність тенденції про вчинення зло­чинів у віці до ЗО років. З метою встановлення наявності чи відсут­ності такої залежності побудуємо паралельні ряди, які охарактери­зують зміну питомої ваги осіб віком до ЗО років. Усі дані братиме­мо відносно 1998 р., оскільки він є початковим. Розрахунок показників наведемо в табл. 23.

Таблиця 23 Дані про зміну злочинності в районі міста (в % до 1998 р.)

Рік
Всього осіб		95,9	71,4	53,5	53,9
У віці до ЗО років		90,9	71,6	59,0	60.9
Питома вага у віці до ЗО років		94,8	100,2	110,2	113,1

Тільки обчисливши всідані відносно 1998 р., можна побачити, що в районі міста дійсно відбувалося «омолодження» злочинності (третій рядок табл. 23). Даний числовий приклад дає змогу зрозу­міти застосування паралельних рядів для статистичного аналізу і складність їх використання. При цьому шляхом попереднього тео­ретичного аналізу слід з'ясувати наявність залежності між показни­ками і за якими критеріями її можна оцінити.

Метод статистичних групувань. Цей метод порівняно з методом середніх та відносних величин має велике значення для вивчення взаємозв'язку між явищами суспільного життя.

Щоб вивчити взаємозв'язок за допомогою методу групувань, необхідно розгрупувати всі одиниці за ознакою, вплив якої треба визначити, і в межах кожної групи обчислити середню величину іншої ознаки, залежної від групувальної ознаки(результативної). Порівнюючи середні значення похідної (результативної) ознаки з ознакою, яку покладено в основу групування, встановлюємо зв'я­зок між ознаками. Отже, поєднання методу групувань з методом середніх дає змогу обчислити групові середні, які використовуються для вимірювання взаємозалежності явищ.

При визначенні залежності будь-якої ознаки не від однієї, а від декількох ознак, треба провести групування за цими ознаками, взяти­ми в сукупності, тобто в комбінації. На базі цього групування слід по­будувати комбінаційну таблицю, в підметі якої будуть групи і підгру­пи, утворені за кількома ознаками, взятими в комбінації, а в присуд­ку — середні розміри ознаки, зумовлені групувальними ознаками.

За допомогою таких групувань можна вивчити зв'язок між зло­чинністю і «фоновими» явищами (алкоголізмом, наркоманією, розпутством тощо), між злочинністю неповнолітніх та їх сімейно-побутовими умовами життя, між злочинністю і рівнем освіти осіб, що вчинили злочини, і т.под. Цей метод дає змогу встановити на­явність чи відсутність зв'язку між явищами, а також загальну тен­денцію цієї залежності. Для проведення таких групувань є достатньо ' даних у статистичній звітності правоохоронних органів.

Наприклад, у табл. 24 наведено дані про роботу 15 суддів місце­вого суду

Використовуючи метод групування, розіб'ємо всі дані на п'ять груп з рівними інтервалами за правилами, викладеними у розділі V даного підручника. Для цього від максимальної кількості розгляну­тих справ (201 справа) віднімемо мінімальну кількість розглянутих справ (26 справ) і одержаний результат поділимо на 5. Інтервали

Таблиця 24 Відомості про кількість розглянутих справ і якість їх розгляду

№ судді	Кількість розглянутих справ	% нескасованих вироків
		79,2
		76,3
		90,2
		88,4
		96,0
		91,0
		83,2
		94,1
		94,2

дорівнюватимуть 35 справам. Після цього шляхом нескладних арифметичних розрахунків одержимо такі дані, які будуть нагляд­но свідчити про залежність якості розгляду справ від завантаженості суддів. Зростання кількості розглянутих справ призводить до зни­ження якості судочинства і, як наслідок, до зростання питомої ваги скасованих вироків (табл. 25).

Метод групувань, як й інші методи, дає змогу встановити на­явність чи відсутність залежності між явищами, а також загальний напрямок цієї залежності.

За допомогою методу статистичних групувань можна встанови­ти вплив двох і більше факторів на зміну результативної ознаки (комбінаційні групування). Групування важливі і для вивчення зв'язків між якісними та кількісними показниками. Але метод гру­пувань та інші розглянуті методи не ставлять своїм завданням

Табл й ця 25 Залежність якості судочинства від завантаженості суддів

Групи суддів за кількістю розглянутих справ	Кількість суддів	Середній відсоток нескасованих вироків на одного суддю
25-60
61-95
96 - 130
131-165
Більше 165
Всього

кількісний вираз щільності зв'язку Це питання розв'язується в ста­тистиці лише за допомогою методів кореляції, розроблених мате­матичною статистикою.

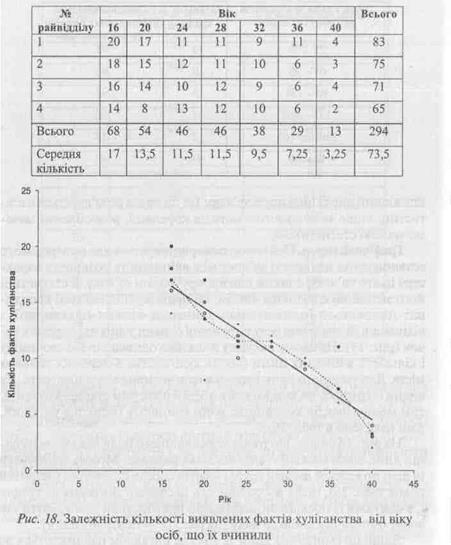
Графічний метод. Цей метод використовується для попереднього встановлення наявності зв'язку між явищами та розкриття харак­теру цього зв'язку, а також для вибору форми зв'язку. В статистиці його застосовують таким чином: на прямокутній системі коорди­нат наносяться індивідуальні значення ознаки (факторної) і відповідні їй значення результативної ознаки у вигляді окремих то­чок (рис. 18). На цьому рисунку показано одночасно вік злочинців і кількість вчинених ними фактів хуліганства в окремих районах міста. Для умовного прикладу ми взяли чотири райвідділи міста. Як видно із графіку, ця залежність є оберненою: чим старше злочинці, тим менше фактів хуліганства вони вчиняють (приклад умовний, дані наведено в табл. 26).

На рис. 18 видно, що точки кореляційного поля лежать не на од­ній лінії, вони витягнуті смугою зліва направо. Можна згрупувати ці дані по кожній віковій групі і знайти середні значення (останній рядок табл. 26), після цього нанести ці середні значення на графік і, з'єднуючи їх послідовно відрізками прямих ліній, побудувати так звану емпіричну лінію зв'язку (на рис. 18 — перервна лінія).

Якщо ця емпірична лінія зв'язку за виглядом наближається до прямої лінії, то можна припустити наявність прямолінійної коре­ляційної залежності між факторною та результативною ознаками. На рис. 18 вона побудована як лінія неперервна. Якщо ж є тенден­ція до нерівномірної зміни значень результативної ознаки і емпі-

Таблиця 26 Дані про кількість виявлених осіб, що вчинили хуліганство

рична крива наближується до якої-небудь кривої, то це може бути пов'язано з наявністю криволінійної кореляційної залежності.

Регресійний та дисперсійний методи аналізу зв'язків. Ці методи покликані вирішити два основних завдання:

1) в результаті економічного аналізу встановити форму зв'язку і дати його математичне вираження за допомогою кореляційних рівнянь;

2) встановити щільність зв'язку між факторною хі результатив­ною у ознаками.

Перше завдання вирішується в ході аналізу того чи іншого яви­ща. Залежно від форми зв'язку, який визначено на основі поперед­нього якісного аналізу, кореляційні рівняння можуть мати різний вигляд. У статистиці використовуються прямолінійні та кри­волінійні кореляційні рівняння.

Теоретичної лінією регресії називають ту лінію, навколо якої групуються точки кореляційного поля і яка вказує основний напря­мок, основну тенденцію зв'язку. Теоретична лінія регресії повинна відображати зміни середніх величин результативної ознаки у відпо­відно до зміни факторної ознаки х.

Якщо попередній аналіз явищ, зв'язок між якими вивчається, показує, що рівним змінам середніх значень факторної ознаки відповідають приблизно рівні зміни середніх значень результатив­ної ознаки, то для вираження форми кореляційного зв'язку мож­на використати прямолінійне кореляційне рівняння

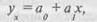
де у^— ординати шуканої прямої, або вирівнювані значення результативної ознаки; х — факторна ознака; а у і а^ — параметри рівняння.

Перший параметр рівняння а у — ордината лінії при х = 0. Па­раметр а^, який називається коефіцієнтом регресії, — це показник середньої зміни ознаки у на одиницю ознаки х в межах даного дослід­ження.

Якщо ми маємо обернену залежність між результативною та факторною ознаками, то рівняння лінійної залежності матиме та­кий вигляд:

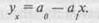
Така лінія регресії побудована на рис. 18. Її параметри матимуть вигляд у = 24,438-0,4978 х.

Для знаходження параметрів рівняння а і а застосовують спосіб найменших квадратів. Сутність цього способу полягає в тому, що знаходять такі значення коефіцієнтів рівняння, при яких

сума відхилень фактичних значень результативної ознаки від обчис­лених за допомогою рівняння буде найменшою з усіх можливих, тобто сума відхилень точок кореляційного поля від відповідних то­чок теоретичної лінії регресії дорівнює нулю.

Якщо попередній аналіз досліджуваних явищ, зв'язок між яки­ми вивчається, показує, що рівним змінам середніх значень фак­торної ознаки відповідають нерівні зміни середніх значень резуль­тативної ознаки, то для вираження загального характеру зв'язку застосовують криволінійні форми кореляційних рівнянь, з яких найчастіше використовуються вирівнювання за параболою і гіперболою.

Прямолінійне кореляційне рівняння має більш широке застосу­вання, тому що його параметри легше обчислити, хоча в реальному житті лінійний зв'язок між явищами суспільного життя зустрічаєть­ся дуже рідко. Але якщо вибрати нетривалий проміжок часу, то яка завгодно крива лінія обов'язково наближується до прямої лінії. Тому вибір прямої лінії можна розглядати як деяке спрощення дійсної за­лежності між явищами та істотне спрощення усіх розрахунків.

Друге завдання кореляційного аналізу — це вимірювання щільності зв'язку, тобто ступеня впливу х на варіацію ознаки у. Щільність кореляційного зв'язку оцінюється за допомогою коефі­цієнта кореляції та кореляційного відношення. Коефіцієнт кореляції — це числова характеристика, що виражає взаємозв'язок і спільний розподіл двох випадкових величин. Він достатньо точно оцінює ступінь щільності взаємозв'язку при наявності лінійної залежності між факторною та результативною ознаками. При наявності криво­лінійної залежності він недооцінює ступінь щільності зв'язку, тому рекомендується використовувати як показник ступеня щільності зв'язку кореляційне відношення. Обчислення кореляційного відно­шення можливо лише за наявності достатньо великої кількості да­них, які наведені, як правило, у вигляді групової таблиці. Обчислення кореляційного відношення при великій кількості груп і малої кількості одиниць у кожній групі позбавлено сенсу.

Індекс кореляції завжди повинен знаходитися в межах від нуля до одиниці. Якщо індекс кореляції дорівнює нулю, то немає ніякого взає­мозв'язку між досліджуваними явищами, інакше кажучи, результатив­на ознака не залежить від зміни цієї факторної ознаки. Якщо індекс кореляції дорівнює одиниці, то це свідчить про наявність повного функціонального зв'язку між явищами, про те, що результативна оз­нака повністю залежить від зміни факторної ознаки.

Чим ближче одержаний результат до одиниці, тим щільніше результативна ознака залежить від факторної, і навпаки.

Індекс кореляції може мати як знак плюс, так і знак мінус. Якщо залежність між показниками пряма, то індекс кореляції має знак плюс; якщо залежність між показниками обернена, то індекс ко­реляції матимемо знак мінус.

Оцінити щільність взаємозв'язку можна лише за допомогою законів математичної статистики. З цією метою застосовуються спеціальні таблиці. На практиці для більшості економічних розра­хунків вважається, що він обов'язково повинен бути більше 0,75, щоб більше, ніж на три чверті зміна результативної ознаки склада­лась під впливом факторної.

За прикладом (табл. 26) коефіцієнт кореляції дорівнює (- 0,97247), тобто вчинення злочину на 97,2 % залежить від віку злочинців. Знак мінус підкреслює, що залежність між факторним показником (віком осіб, які вчинили злочин) і результативною ознакою (вчинення зло­чину) обернена. Якщо в дійсності коефіцієнт кореляції має таке значення, то в цьому разі можна говорити про те, що між показ­никами існує дуже щільний зв'язок, який наближує його до функ­ціонального.

В юридичній науці була здійснена спроба розробити спеціальний коефіцієнт кореляції між показниками судимості та покарання, але ця формула не знайшла поширення, тому ми її не наводимо.

Обчисливши лінійний коефіцієнт кореляції, оцінюючий ступінь зв'язку між змінами факторної та результативної ознак, можна об­числити коефіцієнт регресії, що дає змогу вирішити завдання обгрун­тованого прогнозу тенденцій зміни результативного фактора в май­бутньому Практичне використання рівнянь регресії з метою екстра­поляції можливо лише тоді, коли ми вважаємо, що в майбутньому істотно не зміняться умови формування рівнів ознаки, які лежали в основі обчислення параметрів рівняння регресії. Це ще раз підкрес­лює, що метод екстраполяції на основі рівнянь регресії може засто­совуватися на практиці лише на нетривалий проміжок часу.

Ми зупинилися лише на розгляді питань парної кореляції. В дійсності ж при проведенні статистичного аналізу правових явищ слід вивчати багатофакторні кореляційні взаємозв'язки, тому що на практиці результативний фактор змінюється під впливом декількох причин, факторних ознак. Одночасне вивчення їх впливу прова­диться на основі використання методів множинної кореляції. В цьому випадку можна обчислити часткові та множинні коефіцієн-

ти кореляції, які дають змогу встановити вплив різних факторів на зміну результативної ознаки.

Якщо позначити фактори як Ху Ху Ху..., х^, то лінійне рівнян­ня множинної кореляційної залежності може бути у загальному виг­ляді записано таким чином:

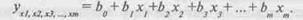
За параметрами цього рівняння можна оцінити внесок кожно­го із факторів у зміну рівня результативного фактора. Коефіцієнти рівняння множинної регресії дають змогу встановити абсолютний розмір впливу факторів на рівень результативної ознаки і характе­ризують ступінь впливу кожного фактора на результативну ознаку при фіксованому (середньому) рівні інших факторів.

З метою порівняння оцінок ролі різних факторів у формуванні результативної ознаки необхідно доповнити абсолютні показники відносними, такими як коефіцієнт еластичності, бета та дельта-коефіцієнти, котрі дають змогу уточнити вплив різних факторів на •гі чи інші результати. Так, частковий коефіцієнт еластичності по­казує, на скільки відсотків у середньому змінюється результативна ознака зі зміною ознаки-фактора (наприклад, першого) на один відсоток при фіксованому стані інших факторів. Бета-коефіцієнт дозволяє порівнювати вплив коливання різних факторів на варіа­цію результативної ознаки, на основі чого виявляються фактори, в розвитку яких закладені найбільші резерви зміни результативної оз­наки. З метою оцінки частки впливу кожного фактора у сумарний їх вплив розраховуються дельта-коефіцієнти. При достатньо значній кількості факторів, які включені до рівняння регресії, про­водиться ранжування факторів за величиною цих коефіцієнтів.

Дата добавления: 2015-04-24