Види статистичної звітності в органах, які ведуть боротьбу з адміністративними правопорушеннями 7 страница

Теорія імовірності — це розділ математики, в якому вивчають­ся тільки випадкові явища (події) з стійкою частотою і встановлю­ються закономірності при їх масовому повторенні.

Одне з головних визначень теорії імовірності — це поняття події. Явища, які розглядаються, з огляду на те, здійснилися вони чи ні, називають подіями. Стосовно подій ставиться таке основне завдання: передбачити, чи з'явиться (здійсниться) досліджувана подія при настанні того чи іншого наперед заданого комплексу факторів.

Якщо при даному комплексі факторів обов'язково відбудеться подія, то вона має назву достовірної події. Якщо при даному ком­плексі факторів подія не може відбутися, то вона іменується немож­ливою подією.

Якщо при даному комплексі факторів подія може відбутися або не відбутися, то вона має назву випадкової події. Інакше кажучи, подія називається випадковою, якщо вона однозначно не визна­чається умовами, в яких протікає, або ми не можемо врахувати всі фактори, які впливають на подію. Наука, що вивчає закономірності масових випадкових подій, і називається теорією імовірності.

Прикладами випадкових подій є народжуваність хлопчика (або дівчини) у конкретній сім'ї; кількість злочинів, учинених за певний проміжок часу, тощо. Кожний окремий злочин — унікальне со­ціально-стихійне діяння з протиправного вирішення суперечнос­тей між людиною і суспільством. Тому ми ніколи не зможемо з аб­солютною достовірністю визначити, де, хто і коли вчинить той чи інший злочин. Злочинність є дзеркалом, в якому ми можемо більш-менш об'єктивно бачити, як функціонує наше суспільство, тому рівень зареєстрованих злочинів є вирішальним фактором при оцінці якості нашого життя.

Застосовувати теорію імовірності можна лише у тих випадках, коли ми внаслідок об'єктивних причин не можемо абсолютно точ­но знати про умови, походження та розвиток явища. Теорія імовір­ності описує лише ті випадкові події, яким притаманні стійкі ча­стоти. Причому чим у менших межах коливаються частоти вихід­них подій, тим точніше теорія імовірності описує досліджуване явище.

Одне з основних понять теорії імовірності — це імовірність. Існують різні підходи до визначення цього поняття. Класичне виз­начення імовірності таке: імовірність випадкової події дорівнює відношенню числа випадків, які сприяють події, до спільного чис­ла можливих випадків. Інакше кажучи, для значної кількості ви­падків імовірність характеризує частоту події.

Кожна подія має числову характеристику у вигляді імовірності. Імовірність завжди знаходиться у межах від 0 до 1 (або у відсотках від 0 до 100%), імовірність випадкової події завжди знаходиться між О та 1, тобто ніколи не дорівнює ні 1, ні 0, оскільки якщо імовірність дорівнюватиме 1, то в цьому випадку ми говоритиме про вірогідність. Нас же цікавить імовірність події, яка наближувати­меться до 1, але в жодному разі імовірність випадкової події не може

дорівнювати 1. і Величина випадкової події характеризується випадковістю, що

', приймає якесь одне значення із деякої множини можливих значень.; Але яким буде це значення, заздалегідь сказати не можна. Інакше кажучи, випадкова величина має цілий набір припустимих значень і в результаті кожного експерименту набуває лише якогось одного

з них.

Найбільш поширений приклад — випадання герба при підки­данні монети. Зрозуміло, що може бути або герб, або ні. Відомо, що французький вчений Буфон наприкінці XVIII ст. провів експери­мент з підкиданням монети 4040 разів, при цьому 2028 разів випав герб. Тобто в його експерименті частота випадання герба дорівню­вала 0,5069 (2028 / 4040) при імовірності 0,5000 (1/2).

Англійський вчений К. Пірсон провів два експерименти: в ході першого він підкидав монету 12 тис. разів, а в ході другого — 24 тис. При першому експерименті він одержав частоту 0,5016, а при дру­гому — 0,5005.

Викладене свідчить про те, що при збільшенні кількості спос­тережень частота все менше відрізняється від імовірності.

§ 2. Поняття закону великих чисел. Динамічні та статистичні закономірності

Закон великих чисел — один із основних законів, який використову­ється статистикою для дослідження явищ суспільного життя. Він

дає змогу зрозуміти, чому із великої кількості хаосу випадкових зв'язків ми можемо встановити і встановлюємо закономірності у розвитку суспільних і природних явищ. Наприклад, народжуваність дівчатка або хлопчиків у кожній окремій родині має випадковий характер: в якихось родинах народжуватимуться одні дівчата, в інших — одні хлопчики, в деяких — пропорційна їх кількість. Але якщо проаналізуємо народжуваність за якийсь значний період (на­приклад, за місяць і більше), то обов'язково встановимо, що на 100 народжених дівчаток припадає 103—104 хлопчики, а іноді й більше (навпаки не може бути ніколи).

Наведений приклад показує, що кожне окреме явище завжди унікальне, оскільки на нього впливає велика кількість випадкових чинників. Розпізнати між ними закономірність у кожному конкрет­ному випадку практично неможливо. Але якщо вивчати ці явища у значній кількості, то можна з'ясувати закономірності, бо випад­кові відхилення, притаманні кожному окремому явищу, в своїй су­купності нейтралізують одне одного. Наприклад, окремий чоловік може прожити довше, ніж окрема жінка, але статистичні дані свідчать про те, що середня тривалість життя чоловіків на 5—6 років менша, ніж у жінок, а коефіцієнт смертності чоловіків у 2—3 рази вищий, ніж у жінок тієї ж самої вікової групи.

Закономірність — це повторюваність, послідовність та порядок у розвитку соціальних явищ. Вона може проявлятися по-різному. В філософії розрізняють два види закономірностей: динамічну та статистичну.

Динамічна закономірність — це така закономірність, яка вияв­ляється в кожному окремому випадку і не залежить від кількості одиниць, які ми спостерігаємо. Вона притаманна природним яви­щам. Наприклад, закон Архімеда можна виявити і на одному. об'єкті, який занурюють в рідину, і на тисячі об'єктів. Аналогічним чином можна виявити закон земного тяжіння та інші фізичні, хімічні та математичні закони.

Статистична закономірність — це така закономірність, яка виявляється лише в достатній кількості однорідних одиничних еле­ментів, котрі й утворюють сукупність. Тобто кожний окремий еле­мент може не підтверджувати існування тієї чи іншої законо­мірності, оскільки існування її в кожному елементі має імовірний характер. Інакше кажучи, статистична закономірність властива лише сукупності одиниць, яка має назву статистичної сукупності.

Статистична сукупність — це певна множина елементів, по­єднаних однаковими умовами існування та розвитку. Об'єктивною основою існування статистичної сукупності є складне перетинан­ня причин та умов, які формують той чи інший масовий процес, наприклад, зміни в тенденціях розвитку злочинності залежно від зміни соціально-економічної та політичної ситуації в країні.

Кожний окремий елемент, який складає статистичну сукупність, має назву одиниці сукупності. Кожна окрема одиниця сукупності є • носієм явища, що вивчається, і відрізняється від іншої одиниці су­купності за розміром ознаки. Завжди має місце коливання (варію­вання) значень ознаки у кожній одиниці статистичної сукупності.

Явищам хімії, фізики, математики та інших природничих наук притаманні лише динамічні закономірності.

Явища суспільного життя, які вивчаються статистикою, нале­жать до статистичних закономірностей. Окремі елементи статис­тичної сукупності характеризуються значною кількістю різних оз­нак, але відповідно до мети дослідження вони мають загальні вла­стивості, що і робить їх статистичною сукупністю. Математично вивчати статистичну закономірність дає змогу використання закону

великих чисел.

Відповідно до цього закону при достатньо великій кількості

досліджуваних одиниць сукупності можна виявити закономірність, яка не залежить від випадку. В разі підсумовування значної кількості одиничних явищ зникають випадкові відхилення і прояв­ляється та чи інша закономірність, яку неможливо було виявити при дослідженні незначної кількості одиниць сукупності.

Закон великих чисел — це математично обґрунтована теорія, відповідно до якої, спираючись на знання теорії імовірності, можна стверджувати, що спільна дія значної кількості випадкових фактів призводить до наслідків, які не залежать від випадку. В разі підсумо­вування значної кількості одиничних явищ обов'язково проявляють­ся порядок і закономірність їх руху і розвитку, які не можна встано­вити при дослідженні малої кількості одиниць сукупності. Інакше кажучи, закон великих чисел дає змогу встановити закономірність там, де на перший погляд проявляється лише випадковість.

З точки зору діалектичного підходу випадковість і необхідність нерозривно пов'язані між собою і завжди переходять одна в іншу, особ­ливо в разі достатньої кількості досліджуваних одиниць сукупності.

Проте закон великих чисел не може визначити ні рівень, ні ди­наміку розвитку суспільного явища. Він лише обумовлює взаємо-

погашення випадкових відхилень, які властиві окремим одиницям статистичної сукупності, дозволяє виявити в ній дію об'єктивних законів розвитку суспільних явищ.

§ 3. Вибірковий метод та його значення для вивчення правових явищ

Вибіркове спостереження є найбільш поширеним видом несуціль-ного спостереження, який застосовують при вивченні різноманіт­них закономірностей суспільного життя. Відмінність його від інших видів несуцільного спостереження полягає в тому, що його прове­дення і поширення результатів на всю масу досліджуваних явищ спираються на використання математики. Застосування його дає можливість значно швидше з меншими витратами часу і ма­теріальних засобів одержати результати. Вибірковий метод дає змо­гу обстежити сімейні бюджети населення, вивчити громадську дум­ку. При дослідженні деяких явищ взагалі можна застосувати тільки його, наприклад, вивчення якості електричних лампочок, якості вина, міцності взуття або схожості зерен.

Сутність вибіркового спостереження полягає в тому, що з усієї сукупності за певними правилами відбирається заздалегідь обумов­лена частина сукупності (кожна четверта, або п'ята, або десята оди­ниця), яка ретельно вивчається. Результати цього часткового спо­стереження поширюються на всю генеральну сукупність з ураху­ванням похибки репрезентативності. При відборі одиниць у вибіркову сукупність повинна бути забезпечена рівна можливість потрапити у вибірку кожної з одиниць сукупності. Порівняно з су­цільним спостереженням вибіркове спостереження має певні пере­ваги, оскільки воно потребує менше коштів і часу для його прове­дення, при цьому також зменшуються й помилки реєстрації.

При проведенні вибіркового спостереження завжди присутня помилка (похибка репрезентативності), оскільки частина завжди відрізняється від цілого. Інакше кажучи, похибка репрезентатив­ності визначає розбіжність між одержаними даними і тими, які б ми мали, якщо б вивчали всі одиниці сукупності без винятку. При­чому вона існує завжди. Спираючи на формули, розроблені теорією імовірності, можна заздалегідь розрахувати її величину.

Отже, основною вимогою до вибіркових спостережень є їх репрезентативність — властивість вибіркового масиву відтворювати

характеристики всієї сукупності. Теорія і практика проведення ви­біркового спостереження показують, що воно при правильній його організації дає достовірні дані, які цілком придатні для використан­ня. Середні та відносні показники, отримані при вибірковому спо­стереженні, досить точно відтворюють відповідні показники всієї сукупності. До вибіркового спостереження внаслідок випадковості відбору одиниць сукупності можуть бути застосовані закон великих чисел і теореми теорії імовірності, що дають можливість обчисли­ти межу помилок, допущених при вибірковому спостереженні.

Вибірковий масив являє собою лише зменшену модель усієї сукупності. Для правильної організації вибіркового спостережен­ня необхідно визначити, в який спосіб відбиратиме одиниці у ви­біркову сукупність, який буде обсяг вибірки і яка за розміром нас задовольнить похибка репрезентативності.

Кількість одиниць сукупності, які відбираються для вибірко­вого спостереження, має бути досить велика. Якщо спостережен­ню піддається занадто мало одиниць, то результати будуть неточ­ними, нерепрезентативними, і в такому випадку можуть бути зроблені неправильні висновки про всю сукупність. Якщо ж відбирається занадто багато одиниць, то відбувається зайва вит­рата сил і засобів для проведення вибіркового спостереження (в цьому разі нівелюється основний зміст вибіркового спостережен­ня). Причому кількість відібраних для вибіркового спостережен­ня одиниць залежить від того, наскільки однорідна чи різнорідна сукупність. Чим більше різнорідна сукупність, тим більше відби­рається одиниць, і навпаки.

Вибіркові дослідження внаслідок низки своїх переваг широко використовуються в різних галузях статистики. Останнім часом усе ширше вони починають застосовуватися при дослідженнях різних правових явищ. Це обумовлено в першу чергу тим, що суцільне спостереження, яке існує у формі звітності, при усіх своїх перева­гах має деякі недоліки. Вона містить лише ті показники, що не­обхідні для повсякденної оперативної роботи. Але якщо необхідно поглиблене вивчення окремих видів злочинів, цивільних і адмініст­ративних правопорушень і особливостей осіб, що їх вчинили, то доцільно вдаватися до вибіркового спостереження.

Грунтуючись на апробованих можливостях вибіркового мето­ду в соціальних дослідженнях, видається за доцільне і важливе його застосування і для вирішення таких завдань, як визначення харак­терних тенденцій, що виявлені при аналізі правових явищ; одер-

жання уявлення про невідображені ознаки генеральної сукупності правових явищ та ін.

При вибірковому спостереженні можуть використовуватися різні джерела: архівні кримінальні та цивільні справи; картки на підсудних; картки на цивільні та адміністративні справи, розглянуті у судових органах, і т.под. Єдине обмеження при відборі джерел інформації — відібрана частина для вибіркового спостереження повинна відображати всю сукупність. Це обмеження є обов'язко­вим для будь-якого вибіркового спостереження, в якій би з галузей господарства воно не проводилося.

Сучасна соціальна обстановка в країні характеризується тим, що ми все частіше зіштовхуємося з окремими унікальними право­вими явищами. Тому безперечно необхідно все більше уваги при­діляти методам вибіркового спостереження, особливо теорії і прак­тиці застосування малої вибірки, коли кількість одиниць у вибір­ковій сукупності менше 25. Необхідність її застосування при дослідженні правових явищ пов'язана з тим, що її можна викорис­товувати в умовах обмеженої інформації. Використовуючи малу вибірку, можна відшукати методи оцінки явищ, інваріантних до за­конів розподілу випадкової величини.

§ 4. Основні положення вибіркового спостереження

При вибірковому спостереженні можуть виникати помилки реєст­рації і похибки вибірки (репрезентативності).

Помилки реєстрації, як і при суцільному статистичному спос­тереженні, являють собою розбіжність між зафіксованими даними в процесі спостереження і дійсними даними. Вони можуть бути випадковими і систематичними. Як правило, помилки реєстрації при вибірковому спостереженні трапляються рідко, тому що знач­но менший обсяг роботи припадає на одного реєстратора, самі реє­стратори завжди більш кваліфіковані, ніж при проведенні суціль­ного спостереження.

Як уже відзначалося, похибки репрезентативності притаманні будь-якому вибірковому спостереженню. Завдання організації пра­вильного проведення вибіркового спостереження — це вибір такої похибки репрезентативності, яка б задовольняла дослідника при даному спостереженні.

Зупинимося на основних термінах вибіркового спостереження. Основні поняття: генеральна і вибіркова сукупності. Генеральна су­купність — це вся сукупність одиниць, з якої проводиться відбір частини одиниць для вибіркового спостереження. Відібрана в пев­ний спосіб частина генеральної сукупності для вибіркового спосте­реження називається вибірковою сукупністю. Узагальнюючі показ­ники генеральної сукупності називаються генеральними, а відповідні показники вибіркової сукупності — вибірковими. Позначення показників генеральної та вибіркової сукупностей на­ведено втабл.13.

Таблиця 13 Позначення показників генеральної та вибіркової сукупності

Показник	Позначення
у генеральній сукупності	у вибірковій сукупності
Кількість одиниць	N	п
Середнє значення ознаки	х	х
Частина одиниць, що мають дану ознаку	Р	\У
Частина одиниць, що не мають даної ознаки	^=1-р	1-У/

. Переваги вибіркового спостереження перед суцільним реалізу­ються лише при додержанні наукових принципів його організації і проведення, насамперед неупередженого, випадкового відбору оди­ниць для спостереження. Вибіркова сукупність повинна повністю відтворювати склад генеральної сукупності. Принцип випадковості відбору забезпечує всім одиницям генеральної сукупності рівні можливості потрапити у вибіркову сукупність.

При проведенні вибіркового спостереження слід спиратися на знання закону великих чисел і теорії імовірності. Але незалежно від того, яким чином проводився відбір одиниць сукупності, завжди будуть розбіжності між характеристиками генеральної і вибіркової сукупностей, пов'язані із сутністю вибіркового методу. Частина завжди відрізняється від цілого. Розбіжності між показниками ге­неральної і вибіркової сукупностей називаються похибками репре­зентативності. Існування їх пояснюється тим, що вибіркова су-

купність не зовсім точно відображає склад генеральної сукупності. Середня в генеральній сукупності відрізняється від середньої у ви­бірковій сукупності на величину похибки репрезентативності:

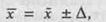
де Д (дельта) — похибка репрезентативності.

Наприклад, після проведення вибіркового спостереження з'я­сувалось, що середній вік рецидивістів дорівнює 32 рокам (х). Розрахована похибка репрезентативності (А) становить +5%, інак­ше кажучи — 1,6 роки (32х5%, або 32 х 0,05 = 1,6). Відповідно до наведеної формули середній вік рецидивістів у всій сукупності (32,0 ± 1,6) коливатиметься в межах від 30,4 до 33,6 років. Таким чином, ми вирішили головне завдання вибіркового спостереження — за здобутими нами вибірковими показниками (одержаними внаслідок проведеного дослідження) з'ясувати, чому дорівнюватимуть відповідні показники генеральної сукупності, які нам невідомі.

Згідно з теоремою Чебишева з уточненнями Ляпунова в мате­матиці було доведено, що при достатньо великій кількості обсте­жених одиниць сукупності середня величина досліджуваної озна­ки у вибірковій сукупності відрізнятиметься від середньої величи­ни в генеральній сукупності на величину

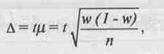
де Д (дельта) — гранична похибка вибірки, тобто похибка репрезентативності; р- (мю) — середня похибка вибірки; / — ко­ефіцієнт, що залежіть від імовірності, з якою можна гарантувати певний розмір похибки репрезентативності. Якщо / = 0, то імовірність також дорівнює 0; якщо 1= 0,5, то імовірність дорівнює 0,383, або 38,3%; якщо ї= 1, то імовірність дорівнює 0,683, або 68,3%; якщо ї= 2, то імовірність дорівнює 0,954, або 95,4%; якщо /= З, то імовірність дорівнює 0,997, або 99,7 %; якщо 1= 4, то імовірність" становить 0,999936 і т.под. При цьому слід враховувати, що даний коефіцієнт може приймати не тільки цілі числа, а й дробові значен­ня (інші умовні позначення містяться у табл. 13).

Із наведеної формули випливає, що похибка репрезентативності залежить від багатьох чинників: імовірності, з якою ми бажаємо одержати результат; кількості одиниць вибіркової сукупності (чим менше одиниць складатиме вибіркова сукупність, тим більше буде;

похибка репрезентативності, і навпаки); однорідності досліджува­ної сукупності (чим більш різнорідною є сукупність, тим більше буде похибка репрезентативності) і від способу відбору одиниць у вибіркову сукупність.

Як правило, при вибірковому спостереженні перед дослідником для успішного його проведення необхідно поставити два взаємопо­в'язаних завдання: 1) визначення необхідної кількості одиниць ви­біркової сукупності, тобто скільки одиниць обстежуватиметься; та 2) розрахунок похибки репрезентативності з встановленим рівнем імо­вірності, тобто межі можливих відхилень вибіркового показника від відповідного показника в генеральній сукупності.

Багаторічна практика свідчить про те, що довірча імовірність 95,4 % (для / = 2) є оптимальною для більшості розрахунків у різних галузях господарства, тим більше для правових явищ. Тому для по­легшення досить громіздких розрахунків похибки вибіркового спо­стереження існують спеціальні таблиці, застосовуючи які можна визначити або величину похибки репрезентативності при певній кількості спостережень з довірчою імовірністю 95,4% (табл. 14), або кількість вибіркових спостережень при заданій величині похибки репрезентативності з довірчою імовірністю 95,4 % (табл. 15) без ви­користання вищенаведених формул. Застосування таблиць (14 або

Таблиця 14 Величина похибки вибірки при даній кількості спостережень

ї	• • " '
Величина показника, %	Кількість спостережень
5(95)	4,4	3,1	2,8	2,5	1,9	1,8	1,6	1,5	1,4	1,4
10 (90)	6,0	4,3	3,5	3,0	2,7	2,5	2,3	2,1	2,0	1,9
15(85)	7,2	5,1	4,1	3,6	3,2	2,9	2,7	2,5	2,4	2,3
20 (80)	8,0	5,7	4,6	4,0	3,6	3,3	3,0	2,8	2,7	2,5
25 (75)	8,7	6,2	5,0	4,3	3,9	3.5	3,3	3,1	2,9	2,7
30 (70)	9,2	6,5	5,3	4,6	4,1	3,7	3,5	3,2	3,1	2,9
35 (65)	9,6	6,8	5,5	4,8	4,3	3,9	3,6	3,4	3,2	3,0
40 (60)	9,9	7,0	5,6	4,9	4,4	4,0	3,7	3,5	3,3	3,1
45 (55)	10,0	7,1	5,7	5,0	4,5	4,1	3,8	3,5	3,3	3,1
	10,0	7,1	5,8	5.0	4,5	4,1	3,8	3.5	3,3	3,2

15) значно спрощує розрахунки і дає змогу швидше одержати ре­зультати. Вперше в навчальній літературі з правової статистики аналогічні таблиці було наведено у підручнику С. Остроумова «Со-ветская судебная статистика» (М., 1970).

Таблиця 14 дає можливість відповісти на питання, яку мінімаль­ну кількість одиниць сукупності необхідно включити до вибірко­вої сукупності, щоб очікуваний результат похибки репрезентатив­ності коливався в установлених межах.

На підставі даних, наведених у табл. 14, видно, що чим більше одиниць потрапляє до вибіркової сукупності, тим менше буде мож­ливою похибка вибірки, і навпаки. Це зрозуміло, бо при значному збільшенні одиниць, які потрапили до вибіркової сукупності, ми проводитиме суцільне спостереження.

Як можна і треба користуватися табл. 14? Наприклад, припус­тимо, що на основі обстеження 200 осіб, яких засуджено за тяжкі насильницькі злочини, було встановлено, що 65% з них вчинено в стані алкогольного сп'яніння. Нас цікавить, наскільки достовірним є цей результат, тобто в яких межах коливається дане значення в усій генеральній сукупності.

Заданими табл. 14 визначаємо, що на перетині горизонтального рядка з числом 65 з вертикальною другою графою з числом 200 зна­ходиться число 6,8. Це означає, що частка засуджених, що вчини­ли тяжкі насильницькі злочини в стані сп'яніння, може коливати­ся в межах від 58,2 % до 71,8 % (65% ± 6,8 %).

Якщо табл. 14 відсутня, то в цьому випадку всі розрахунки необхідно проводити на базі раніше наведеної формули (с. 212). Так, для приклада, який наведено і обчислено за допомогою табл. 14, де і = 2; и¹ = 0,65; п = 200, ми одержимо похибку ре­презентативності внаслідок такого розрахунку:

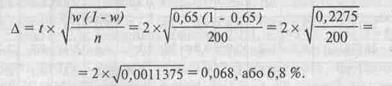
У конкретно-правових дослідженнях, як правило, відсоток по­хибки середнього значення задається самим дослідником на основі програми спостереження і відповідно до даних раніш проведених досліджень. Як правило, вважається допустимою гранична похиб­ка вибірки (похибка репрезентативності) в межах 3 — 5 %.

Якщо допустити похибку вдвічі більшу, то обсяг вибірки можна зменшити в чотири рази, і навпаки, якщо необхідно зменшити по­хибку вибірки вдвічі, то обсяг вибірки треба збільшити в чотири рази.

Слід звернути увагу на те, що табл. 14 побудовано для власне випадкового способу відбору одиниць у вибіркову сукупність, тому її з більшим ступенем вірогідності можна використовувати при ме­ханічному і типовому способах відбору одиниць у вибіркову су­купність. При серійному (гніздовому) способі відбору одиниць у вибірку використовувати дані, наведені в таблицях 14 і 15, не мож­на. (Більш докладно способи відбору одиниць у вибіркову сукуп­ність викладено в наступному підрозділі цього розділу підручника.)

Найважливіше завдання при проведенні вибіркового дослід­ження правових явищ — це визначення репрезентативного обсягу вибіркового спостереження, тобто скільки необхідно проаналізу­вати одиниць з генеральної сукупності, щоб одержана випадкова похибка середнього значення досліджуваної ознаки не перевершу­вала визначеної величини похибки репрезентативності з достат­ньою імовірністю.

Спираючись на математичні теореми закону великих чисел, можна встановити, що при зменшенні обсягу вибірки в декілька квадратів разів похибка середнього значення збільшується в стільки ж разів, і навпаки, зменшення похибки середнього значення вибір­ки в декілька разів призводить до збільшення обсягу вибірки в стільки ж квадратів разів. Отже, визначення величини похибки се­реднього значення ознаки для встановлення обсягу вибірки є дуже важливим.

При практичному застосуванні формул дослідник завжди сти­кається з тим, що необхідні дані про коливання ознаки в гене­ральній сукупності. Як правило, на практиці для визначення обсягу вибірки вдаються до даних попередніх досліджень або проводять так звані пробні обстеження і на їх основі визначають орієнтовні розміри коливання ознаки.

Взагалі слід пам'ятати, що головне при організації вибіркового спостереження — це доведення його обсягу до допустимого мініму­му. При цьому не слід прагнути до надмірного зменшення меж по­хибки вибірки, бо це може призвести до невиправданого збільшен­ня обсягу вибірки і, отже, до підвищення витрат на проведення вибіркового спостереження. В той же час не можна і надмірно збільшувати розмір похибки репрезентативності, оскільки в цьому випадку хоча і відбудеться зменшення обсягу вибіркової сукуп-

ності, але це призведе до погіршення достовірності одержаних ре­зультатів.

Наведемо приклад визначення чисельності вибірки на основі табл. 15. Припустимо, що величина досліджуваного показника до­рівнює 40 % (частка (питома вага) тяжких злочинів в області), а похибка репрезентативності, яку вважаємо допустимою при дано­му дослідженні, не повинна перевищувати ± 4 %. За табл. 15 визна­чаємо, що мінімальний обсяг вибіркової сукупності повинен склас­ти 600. Отже, щоб наше вибіркове дослідження було репрезентатив­ним з довірчою імовірністю в 95,4 % за наших вихідних даних, нам необхідно обстежити як мінімум 600 засуджених.

Дата добавления: 2015-04-24