Види статистичної звітності в органах, які ведуть боротьбу з адміністративними правопорушеннями 6 страница

2) якщо від кожного значення варіанта відняти якесь число, то середня арифметична величина зменшиться на те ж саме число;

3) якщо до кожного значення варіанта додати якесь число, то середня арифметична величина збільшиться на те ж саме число;

4) якщо кожне значення варіанта поділити на якесь число, то середня арифметична величина зменшиться на те ж саме число разів. Ця властивість дає змогу значно простіше обчислити серед­ню арифметичну величину;

5) якщо кожне значення варіанта помножити на якесь число, то середня арифметична величина збільшиться на те ж саме число разів;

6) якщо всі частоти (ваги) поділити (або помножити) на якесь число, то середня арифметична величина від цього не зміниться. Цією властивістю часто користуються, коли частоти (ваги) виража­ються у відсотках до підсумку.

Дуже рідко в правовій статистиці застосовується середня гармо­нічна — обернена величина середньої арифметичної із обернених значень варіантів. Застосування середньої арифметичної, або гар­монічної, залежить від первинних даних. Якщо за ваги (частоти) береться не кількість одиниць сукупності, а величини, одержані внаслідок множення значень варіантів на кількість одиниць, тоб­то зразу маємо добуток х/, то в цьому разі обчислюється середня гар­монічна. У правовій статистиці, як правило, такі дані не зустріча­ються або зустрічаються дуже рідко. В інших галузях статистики ця величина застосовується для обчислення середньої врожайності, середньої продуктивності праці, середнього відсотка виконання плану тощо. До цього часу статистики так і не визначилися, за якою середньою слід обчислювати середній строк будівництва. За прави­лами математичної статистики (мажорантності середніх величин) середня арифметична завжди більша за середню гармонічну, особ­ливо якщо йдеться про значний розмір показника.

Для розрахунку середньої величини за формулою середньої гар­монічної зваженої необхідно виходити з логічного усвідомлення вихідних величин. Наприклад, кількість оштрафованих осіб — це складова частина загальної суми штрафу. Тому, щоб встановити се­редній розмір штрафу (розрахункова величина), ми повинні його обчислити за формулою середньої гармонічної зваженої.

Але може обчислюватися і середня гармонічна проста за фор­мулою

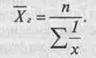
Ця формула використовується лише тоді, коли вага кожного варіанта дорівнює одиниці. На практиці таке практично не зустрі­чається.

Середня гармонічна зважена обчислюється за формулою

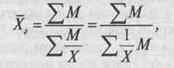
де X— значення варіюючої ознаки; М=ХС— результат перемно­ження значення варіантів на їх ваги.

Якщо ми дійсно будемо розраховувати середній розмір стягну­тих штрафів тим чи іншим органом або в тій чи іншій місцевості, то знаменник дробу матиме реальний зміст — кількість оштрафо­ваних осіб, які сплатили штраф.

Техніку обчислення середньої геометричної і середньої хроноло­гічної, які в правовій статистиці застосовуються при обчисленні по­казників у рядах динаміки, наведено у розділі Х цього підручника.

§ 3. Поняття моди та медіани

Крім математично обчислених степенних середніх величин, у ста­тистиці застосовуються показники описового характеру — струк­турні середні, з яких найчастіше використовуються мода та медіа­на, котрі у впорядкованому ряду розподілу характеризують значен­ня тенденцій окремих варіантів.

Модою в статистиці називається таке значення ознаки, яке зу­стрічається найчастіше. Якщо дані розташовані у вигляді дискрет­ного ряду розподілу, то модою буде значення того варіанта, який має найбільшу частоту. Мода в статистиці застосовується тоді, коли слід охарактеризувати показник, який найчастіше зустрічається в сукуп­ності. Наприклад, при вивченні цін на ринку встановлюємо ціни,

які зустрічаються найчастіше; при встановленні найбільш ходово­го розміру взуття і одягу визначаємо той, який користується най­більшим попитом. Ці показники дають змогу спланувати, які това­ри необхідно виробляти в більшій кількості, а також які товари поставляти на ринок і за якими цінами.

Але в правовій статистиці такі показники застосовуються лише для опису сукупності, а не для наукової характеристики явища. Наприклад, маємо такі первинні дані про вік осіб, що вчинили зло­чини проти особи, в районі міста за місяць: 17, 25, ЗО, 31, 27, 28,15, 18, 21, 22, 25, 24, 16, 24, 26, 19, 32, 35, 19, 17, 20, 21, 22, 23, 22, 26 (дані вибрані з первинних облікових документів без їх оброблення). Порядок заповнення документів первинного обліку дає змогу по­значити тільки ціле число повних років життя. Тому в цьому разі ми можемо обчислювати моду за принципом дискретного ряду розпо­ділу, хоча первинні дані належать до інтервального варіаційного ряду. Мода в нашому прикладі дорівнюватиме 22 роки, оскільки цей показник зустрічається найчастіше (тричі).

В інтервальному варіаційному ряду розподілу легко відшуковуєть-ся лише модальний інтервал, а сама мода визначається приблизно. Формула обчислення моди в інтервальному ряду має такий вигляд:

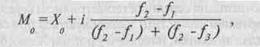
де Му — мода; Хд — нижня межа модального інтервалу; (— ве­личина модального інтервалу;/ — частота інтервалу, який передує модальному;/, — частота модального інтервалу;/, — частота інтер­валу, який йде після модального.

За даними табл. 10 обчислимо моду. Модальний інтервал стано­вить від 18 до 24 років, оскільки йому відповідає максимальна час­тота (48 засуджених). Тоді мода матиме такий вигляд:

Медіаною в статистиці називають значення варіанти, яка ділить впорядкований ряд розподілу на дві рівні за чисельністю одиниць сукупності частини і знаходиться у середині ряду.

Якщо всі значення дискретного ряду записати в певному поряд­ку (зростання або зменшення значення показників), то це буде зна­

чення, яке знаходиться у середині ряду. За наведеним раніш прикла­дом обчислимо медіану. Спочатку впорядкуємо дані про вік осіб, що вчинили злочини проти особи, розташувавши дані в ранжованому порядку зростання показників віку: 15, 16, 17, 17, 18, 19, 19, 20, 21,

I 21, 22, 22, 22,23,24,24, 25,25, 26,26,27,28,30, 31,32, 35. Якщобми мали непарну кількість одиниць ряду, то центральна з них і була б медіаною. В нашому ж прикладі наявне парне число одиниць сукуп­ності. Тоді медіана обчислюється як середня арифметична проста

; двох центральних варіантів або за формулою (2/+ 1): 2. До загаль­ної кількості одиниць сукупності необхідно додати одиницю і одер-

; жане число поділити на 2. В нашому прикладі було наведено 26 осіб, що вчинили злочини. За наведеною формулою знаходимо місце ме-

^ діани: (26 + 1):2 = 13,5. Медіана знаходиться посередині між 13 і 14 значеннями і дорівнює 22,5 рокам, тобто між 22 і 23 роками.

, Складніше обчислюється медіана у варіаційному ряду. Існує така формула для її знаходження:

де М — медіана; х^ — нижня межа медіанного інтервалу; / — величина медіанного інтервалу; ї/— сума частот ряду; 8^, — сума накопичених частот інтервалу, що передує медіанному; / — час­тота медіанного інтервалу.

За якою б формулою не обчислювали медіану, сутність її не змінюється. Медіана в будь-якому випадку повинна поділити ва­ріаційний ряд на дві рівні частини за сумою частот. Тому спочатку в інтервальному ряду розподілу знаходимо інтервал, в якому розта­шована медіана, а потім приблизно обчислюємо саму медіану. За даними табл. 10 обчислимо медіану. З'ясовуємо, що інтервал, в яко­му знаходиться медіана, дорівнює від 18 до 24 років. Потім за на­веденою формулою обчислюємо медіану:

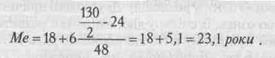
Медіана як показник має перевагу перед іншими видами се­редніх величин, тому що вона не залежить від наявності чи відсут-

ності показників в окремих інтервалах. На її розмір впливає лише порядок розташування показників, а також те, наскільки вірно побудовано ряд розподілу. В такому разі її обчислення нескладне.

Слід зауважити, що мода і медіана є специфічними видами се­редніх величин, оскільки вони завжди характеризують лише центр

розподілу статистичної сукупності.

Моду, медіану та середню арифметичну слід завжди використо­вувати у сукупності, бо вони характеризують ряд розподілу не­однозначне. Якщо ряд симетричний, то вони повністю збігаються.

В нашому прикладі мода дорівнює 22 рокам, медіана — 22,5 рокам, а середній вік, який обчислюється за середньою арифметич­ною, — 23,3 рокам (додаємо всі первинні дані (15 + 16 + 17 +... + 35 = 605) і ділимо їх на кількість осіб — 26). Наведений ряд розпо­ділу має асиметрію, але незначну. За даними табл. 10 маємо такі результати: середній вік — 26,3 роки; мода — 21,4 роки; медіана — 23,1 роки, тобто цей ряд має значно більшу асиметрію.

§ 4. Показники варіації та способи їх обчислення

Середні величини мають велике теоретичне і практичне значення, оскільки вони дають змогу однією величиною охарактеризувати сукупність однотипних явищ. Проте для всебічної характеристики таких явищ їх недостатньо. Статистичній сукупності притаманні коливання у кожній окремій одиниці, які у математиці називаються варіацією. Ці коливання обумовлені тим, що статистичні сукуп­ності виникають та існують під впливом багатьох взаємопов'язаних причин. Деякі автори вважають, що на злочинність впливають від

230 до 250 різних факторів.

Причини, які впливають на суспільні явища, можуть бути ос­новними та другорядними. З точки зору діалектики основні причи­ни формують сукупність і впливають на середні показники, а також на знаходження центру розподілу. Другорядні причини обумовлю­ють варіацію ознак, їх спільну дію, напрямки розвитку явища.

Істотним при цьому є те, що повністю дати оцінку явищу за допомогою тільки середніх показників неможливо: коливання ок­ремих ознак у різних сукупностях можуть бути значними і незнач­ними, а середні величини при цьому будуть однаковими. Для

підтвердження цієї тези наведемо дані про розподіл засуджених за двома різними складами злочинної діяльності за строками позбав­лення волі(табл.11).

Таблиця 11

Розподіл засуджених за строками позбавлення волі за двома складами злочинної діяльності

Приклад № 1	Приклад № 2
Строк позбав­лення волі, рік, Х	Кількість засуджених, /	Добу­ток, X/	Строк позбав­лення волі, рік, Х	Кількість засуджених, /	Добу­ток, хґ
	5	5		ЗО	90
б
Всього			Всього

| В обох прикладах ми взяли по 100 осіб засуджених. У кожному з них середній строк позбавлення волі, який обчислено за серед­ньою арифметичною зваженою, має однакове значення, котре до­рівнює 6 рокам (600: 100). Однак навіть на перший погляд видно, що сукупності є різними. В першій сукупності більшість осіб дійсно одержала середній строк позбавлення волі, в другій — навпаки, більшість осіб одержали мінімальні та максимальні строки позбав­лення волі за цим складом злочинів.

„ Щоб встановити, як відрізняються наведені сукупності, а також | які межі коливання має ознака, необхідно обчислити такі показни-| ки варіації: розмах варіації, середнє лінійне відхилення, середнє ^г квадратичне відхилення і коефіцієнт варіації. Кожний з цих показ­ників має певні аналітичні переваги при вирішенні тих чи інших завдань статистичного аналізу.

Розмах варіації — це різниця між найбільшим і найменшим зна­ченнями ознаки у сукупності. Залежно від того, в якому вигляді наведено первинні дані, техніка обчислення цього показника є різною: це може бути різниця між верхньою межею останнього

інтервалу і нижньою межею першого інтервалу або різниця між середніми значеннями цих інтервалів. Розмах варіації обчислюєть­ся за формулою

К=х —х,

тах тія

де К — розмах варіації; х^— найбільше значення ознаки в су­купності; х^— найменше значення ознаки в сукупності.

За даними табл. 11 в прикладі № 1 розмах варіації склав 10 років (11 — 1), а в прикладі №2 — 6 років (9 — 3).

Розмах варіації відображає тільки крайні значення ознаки, тому він є головним показником у тих випадках, коли варіанти повто­рюються один раз. В інших випадках розмах варіації застосовуєть­ся для того, щоб одержати загальне уявлення про варіацію ознаки у всієї сукупності. Наприклад, розмах варіації віку у студентів різних форм навчання має бути різним, але він завжди буде меншим за розмах варіації віку всього населення певного регіону. В деяких регіонах він може бути більше 100 років.

Безумовною перевагою цього показника як міри оцінки коли­вання ознаки можна вважати нескладність його обчислення і ро­зуміння. Але його недоліком є те, що він оцінює лише крайні ко­ливання ознаки, а вони можуть бути для сукупності випадковими і не відображати розподіл відхилення ознаки в сукупності. У зв'яз­ку з цим надійність даного показника є невисокою, але його часто використовують для попередньої оцінки варіації при статистичних

розрахунках.

Так, у прикладі № 1 60 % осіб засуджено на строк, який збігаєть­ся з середнім строком позбавлення волі; в прикладі № 2 — їх лише 20 %, але розмах варіації в прикладі № 2 менший, ніж у прикладі №1, що не відповідає ні логіці, ні дійсності.

За даними табл. 9 розмах варіації дорівнює 4 особам (5 — 1); за даними, які застосовані для розрахунку медіани, — 20 рокам (35 — 15). Це ще раз підтверджує висновок про те, що розмах варіації істотно залежить від значень ознаки і дає лише приблизну харак­теристику наявності коливань ознаки в сукупності.

Для характеристики реального розподілу відхилень окремих значень одиниць сукупності від середньої величини застосовуються середнє лінійне та середнє квадратичне відхилення.

Середнє лінійне відхилення — це арифметична середня з абсо­лютних значень відхилень ознаки окремих варіантів від їх середньої

арифметичної. Середнє лінійне відхилення обчислюється за фор­мулою

де Л — середнє лінійне відхилення; х — значення ознаки; х — середнє значення ознаки;/— частота (вага) кожного варіанта.

При обчисленні цього показника відхилення від середньої ве­личини однаково оцінюються як в більший, так і в менший бік. Це є не зовсім вірним з точки зору економічного аналізу, оскільки нас завжди цікавлять зрушення і зміни в сукупності в якійсь-то один бік і ми дуже обережно ставимося до змін в іншій бік. Наприклад, незначні строки покарання свідчать про те, що особами вчинено менше тяжких злочинів.

У табл. 12 наведено розрахунок середнього лінійного та серед­нього квадратичного відхилень.

Таблиця 12

Розрахунок середнього лінійного та середнього квадратичного відхилень

Приклад № 1	Приклад № 2
• х	/	X- X	(Х-Х)/-	(х-х)^2/	X	/	X- X	(х-х)/	(х-х)^
1		-5	-25				-3	-90
		-2	-30				-1	-10
Всього		-			Всього		—

На підставі даних, наведених у табл. 12, видно, що для обчислен­ня середнього лінійного відхилення слід брати абсолютне значення показників. Якщо підсумувати всі значення з урахуванням знака, то в четвертому та дев'ятому стовпчиках табл. 12 одержимо нуль. З точки зору математики одержання нуля є обов'язковим, які б первинні дані ми не мали. Для статистики нульовий результат не має сенсу.

Обчислимо за даними табл. 12 середнє лінійне відхилення для прикладу №1—1,1 роки (підсумуємо всі дані, наведені в четверто-

му стовпчику, незважаючи на знак перед числом, тобто 25 + ЗО + 0 + 30+25, цю суму слід поділити на загальну кількість засуджених осіб — 100 чол.); для прикладу № 2 — 2,0 роки ((90 +10+0+10 +90): 100) — за даними, наведеними у дев'ятому стовпчику. Одержані дані по­казують, що друга сукупність має більші коливання, ніж перша.

Найчастіше при економічних розрахунках для оцінки щільності взаємозв'язку явищ, обчислення похибки репрезентативності тощо використовується середнє квадратичне відхилення.

Середнє квадратичне відхилення — це корінь квадратний із середнього квадрату відхилень ознаки кожного варіанта від їх се­редньої арифметичної. Цей показник обчислюється за формулою

де а — середнє квадратичне відхилення; х — значення ознаки;

х — середнє значення ознаки.

Щоб його знайти, достатньо суму п'ятого і десятого стовпчиків табл. 12 поділити на загальну кількість показників і з одержаної

величини добути корінь квадратний.

Середнє квадратичне відхилення в прикладі №1 дорівнює 1,92 рокам (370 ділимо на 100 і добуваємо корінь квадратний), в при­кладі №2 — 2,37 рокам. Отже, середнє квадратичне відхилення дає ' змогу встановити, що друга сукупність (приклад №2) має значно більші коливання ознак — в 1,23 рази (2,37: 1,92).

Всі наведені показники (розмах варіації, середнє лінійне і се­реднє квадратичне відхилення) дають змогу встановити і оцінити міру коливання ознак в абсолютному розмірі, тому всі вони обо­в'язково мають точно такі ж одиниці виміру, як і одиниці сукуп­ності. Для роз'яснення техніки обчислення показників варіації і були взяті дві однакові з точки зору одиниць виміру сукупності,

тому їх можна і порівнювати між собою.

Недоліком середнього квадратичного відхилення є те, що воно характеризує тільки абсолютну міру коливання ознаки. Якщо об­числювати середнє квадратичне відхилення за даними табл. 9, то можна одержати показник 1,28 чол. В цьому разі порівнювати його

з показниками наших прикладів не можна.

Між середнім лінійним, середню величиною і середнім квадратич­ним відхиленням існує такий зв'язок: 1,25 Л = О, а а'= 1/3 х. В си­

метричних рядах розподілу середнє квадратичне відхилення можна визначити за формулою а = 1/6 (х —х.), або ж (7 = 1/6 К.

Розрахунок середнього квадратичного відхилення має логічний зміст лише в тому разі, коли фактичний розподіл ознаки близький до нормального. Для явно асиметричних розподілів його розраху­нок не має сенсу.

Квадрат середнього відхилення іменується дисперсією. Значен­ня цього показника істотно зростає, коли необхідно обчислити ва­ріацію альтернативної ознаки. Як вже підкреслювалось, альтерна­тивна ознака — це така ознака, яку кожна одиниця сукупності або має, або не має, наприклад, наявність наукового ступеня у викла­дачів вищого навчального закладу.

Кількісно варіація альтернативної ознаки виражається двома значеннями: наявність ознаки позначається через одиницю, а її відсутність — через нуль. Позначивши частку одиниць, які мають дану ознаку, через р, а одиниці, які не мають цієї ознаки, через ^ = (1 — р), визначимо середню арифметичну альтернативної ознаки. Вона дорівнюватиме

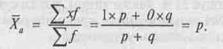
Після цього обчислимо дисперсію альтернативної ознаки:

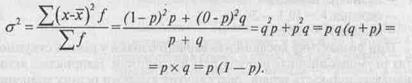
Отже, частка для альтернативної ознаки замінює середню ве­личину, а дисперсія є добутком частки на доповнення її до оди­ниці. Значення дисперсії альтернативної ознаки та її максималь­ного значення необхідне для обчислення похибки репрезента­тивності при вибірковому спостереженні (див. розділ IX цього підручника).

Для більш детальної характеристики сукупності застосовуєть­ся відносний показник — коефіцієнт варіації. Існують різні думки щодо того, за яким показником його можна обчислювати. На прак­тиці коефіцієнт варіації завжди порівнюють за допомогою серед­нього квадратичного відхилення, яке найбільш реалістично відоб­ражає коливання ознаки в сукупності.

Коефіцієнт варіації — це відсоткове відношення середнього квадратичного відхилення до середнього рівня. Як правило, цей середній рівень обчислюється за формулою середньої арифметич­ної. Коефіцієнт варіації обчислюється за формулою

де V— коефіцієнт варіації; а — середнє квадратичне відхилен­ня; X— середній розмір ознаки в статистичній сукупності.

За даними табл. 12 коефіцієнт варіації в прикладі № 1 дорівнює 32,0 % (1,92: 6 х 100), в прикладі №2 - 39,5 % (2,37: 6 х 100); за даними табл. 9 — 53,3 % (1,28: 2,4 х 100).

Коефіцієнт варіації дає змогу порівняти різні сукупності. Чим менше цей показник, тим менше коливання ознаки в сукупності, і тим більш однорідною є сукупність, і навпаки.

Показник коефіцієнта варіації слід використовувати для оцін­ки однорідності сукупності. Існує оціночний критерій — сукупність однорідна і середня величина в ній є типовою, якщо коефіцієнт варіації не перевищує 33 %. Таким чином, тільки сукупність, наве­дена в прикладі №1, є однорідною, хоча в ній розмах варіації був значно більшим, ніж в інших сукупностях.

Розрізняють такі значення відносних коливань (варіації):

- незначна варіація V ^ 10 %

- середня У= 10,1 — ЗО %;

- велика У> ЗО %.

При розрахунку коефіцієнта варіації ознаки у різних сукупно­стях та умовах виникає необхідність його оцінки. Наприклад, якщо вивчають кількість справ, розглянутих суддями різних місцевих судів за певний період (місяць, рік), кількість осіб, засуджених по­вторно, в різних виправних установах тощо, то істотність різниці коефіцієнтів варіації розраховують за формулою

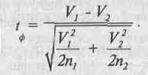
Різницю коефіцієнтів варіації вважають невипадковою, якщо критерій згоди і > 3, якщо ж і. < 3, роблять висновок, що при цій кількості спостережень нульова гіпотеза не підтверджується, і тому істотна різниця не доведена.

Питання та завдання для самоконтролю

1. Дайте визначення поняття середньої величини.

2. Визначте головну мету обчислення середніх вели­чин.

3. Назвіть аспекти, які потрібно враховувати при обчисленні середніх величин.

4. Назвіть види середніх величин.

5. Напишіть формули обчислення середньої ариф­метичної.

6. Назвіть основні властивості середньої арифме­тичної.

7. З якою метою використовується середня гармо­нічна?

8. Поясніть, в чому різниця між степенними і струк­турними середніми.

9. Дайте визначення понять моди та медіани і на­ведіть приклади їх використання в правовій ста­тистиці.

10. Що таке варіація ознак? Розкрийте показники варіації статистичної сукупності: розмах варіації, середнє лінійне та середнє квадратичне від­хилення, коефіцієнт варіації.

Завдання І. Працівниками органу досудового слідства було розслідувано в строк до 1 місяця 420 кримінальних справ; в строк від 1 до 2 місяців — 632 справи; в строк від 2 до 3 місяців — 75 справ; в строк понад 3 місяця — 15 справ. Визначте середній строк досудового слідства і вкажіть, який різновид середньої величини Вами застосовано і чому.

Завдання 2. Визначте середньомісячне наванта­ження на одного слідчого, якщо у відділі, де за штат­ним розкладом 22 слідчих, знаходилося у вироб­ництві: у січні — 160 справ, у лютому — 175 справ, у березні — 188 справ, у квітні — 155 справ, у травні — 182 справи, у червні — 190 справ. Вкажіть, який вид середньої Вами обчислено і чому.

Завдання 3. Розподіл 450 адміністративних право­порушень за сумою штрафу має такий вигляд: до 60 грн. — 50 правопорушень; 60 — 70 грн. — 100; 70 — 80 грн. — 140; 80 — 90 грн. — 90; 90 грн. і більше — 70. Визначте середню суму штрафу, яка припадає на одне

адміністративне правопорушення, а також показни­ки її варіації. Який вид середніх величин Вами обчис­лено? Зробіть висновки.

Завдання 4. Розподіл 200 цивільних справ за вар­тістю позову має такий вигляд: до 100 грн. — 20 справ;

100 - 200 грн. - 60; 200 - 400 грн. - 80; 400 - 600 грн. — 30; 600 грн. і більше — 10. За наведеними да­ними обчисліть середню вартість позову і показники варіації. Який вид середніх величин Вами обчислено? Зробіть висновки.

Завдання 5. Маємо такі дані про вік засуджених, що вчинили крадіжку особистого майна громадян у травні цього року: 24, ЗО, 25, 28, 23, 24, 22, 24, 21, 20, 30,27, 26, 21, 23, 24,28. На основі цих даних обчисліть моду, медіану та середній вік засуджених за цією ка­тегорією справ. Зробіть висновки.

Завдання 6. Маємо такі дані про вік осіб, що вчи­нили хуліганство у лютому цього року: 18, 20, 19, 18, 21, 22, 23, 24, 25, 18, 20,26. За цими даними обчисліть моду, медіану та середній вік осіб, що вчинили злочи' ни по цій категорії справ. Зробіть висновки.

Завдання 7. За даними, наведеними в завданні 5, обчисліть показники варіації. Зробіть висновки.

Завдання 8. За даними, наведеними в завданні 6, обчисліть показники варіації. Зробіть висновки.

Основні положення теорії ЇХ імовірності та вибіркового спостереження

§ 1. Основні поняття теорії імовірності

У своїй практичній діяльності ми завжди стикаємося з явищами, результат дії яких важко, а іноді і неможливо передбачити, оскіль­ки наслідки цього залежать від випадку. Наприклад, який застра­хований об'єкт буде знищено внаслідок стихійного лиха — справа випадку. Але страхові органи керуються в своїй діяльності передба­ченням не кожного окремого об'єкта, а значної кількості об'єктів. При вивченні їх у великій кількості можна передбачити їх стан у майбутньому. Тому при статистичному обробленні емпіричних да­них використовують певні визначення і правила, встановлені тео­рією імовірності.

Теорія імовірності — це математична наука, яка виникла усере­дині XVII ст. Першими працями, в яких наводилися основні по­няття теорії імовірності, прийнято вважати роботи французів Б.Паскаля (1623—1662), П. Ферма (1601—1665) і голландця X. Гюй-генса (1629—1695). Подальший розвиток теорії імовірності пов'я­зують з ім'ям швейцарського математика Я.Бернуллі (1654—1705), котрий у 1713 р. вперше в елементарному вигляді довів теорему, яка в подальшому була названа законом великих чисел.

У XIX ст. теорія імовірності з успіхом застосовується в страховій справі, статистиці народонаселення, біології і військових науках, особливо в артилерії. В цей період вона збагачується працями П. Лапласа (1749-1827), К. Гаусса (1777-1855), С. Пуассона (1784-1840) та ін.

Значний внесок у розвиток теорії імовірності здійснили ро­сійський вчений П. Чебишев (1821—1894) та його учні А. Марков (1892—1922) і О. Ляпунов (1857—1918). Своїми працями вони пе­ретворили теорію імовірності на систематизовану і чітку математич­ну науку.

Зараз цю науку використовують у всіх галузях знань, де дослід­жуються прояви випадкових явищ зі стійкою частотою, наприклад, народжуваність дівчаток або хлопчиків на певній території за три­валий проміжок часу.

Дата добавления: 2015-04-24