
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Расчеты частот, мощностей и вращающих моментов на отдельных элементах привода
|
|
|
|
Кинематический расчет
Общее передаточное число привода равно:
 .
.
При разбивке общего передаточного числа редуктора по ступеням воспользуемся рекомендациями табл. 10 для зубчато – червячного редуктора, согласно которым передаточное число тихоходной ступени определяется зависимостью
 при
при 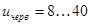 .
.
Принимаем: 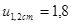 .
.
Тогда 
Из стандартного ряда (см.табл.10) назначаем 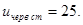
Фактическое передаточное число редуктора равно:
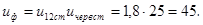
Процент ошибки фактического передаточного числа редуктора относительно номинального согласно формуле (12)
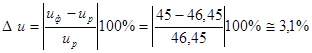 .
.
Поскольку при [Du]=4% выполняется условие (13) 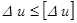 , можно сделать заключение о том, что кинематический расчет выполнен удовлетворительно.
, можно сделать заключение о том, что кинематический расчет выполнен удовлетворительно.
· Частота вращения входного вала редуктора и установленной на этом валу шестерни быстроходной ступени равна частоте вращения вала электродвигателя:
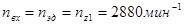 .
.
· Частота вращения промежуточного вала редуктора и закрепленных на нем колеса быстроходной ступени и червяка тихоходной ступени
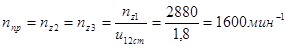 .
.
· Частоты вращения выходного (тихоходного) вала двухступенчатого редуктора, ведомого червячного колеса тихоходной ступени и ведущей звездочки цепной передачи равны:
 .
.
· Мощности, передаваемые отдельными элементами привода:
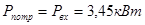 ;
;
 ;
;
 ;
;
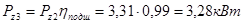 ;
;
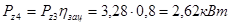 ;
;
 .
.
· Вращающие моменты:
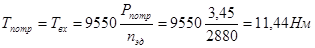 ;
;
 ;
;
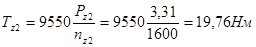 ;
;
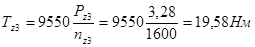 ;
;
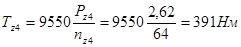 ;
;

Результаты расчетов приведены в табл. 17.
Таблица 17 – Результаты кинематического расчета
| Параметры | Электродвигатель | Редуктор | Цепная передача | |||
| I ступень | II ступень | |||||
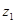
| 
| 
| 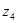
| |||
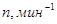
| ||||||
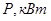
| 3,45 | 3,42 | 3,31 | 3,28 | 2,62 | 2,6 |

| 11,44 | 11,34 | 19,76 | 19,58 | ||
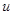
| - | 1,8 | 1,8 |
1.8 Выбор салазок для электродвигателя
Для обеспечения возможности регулирования натяжения ремня в ременной передаче электродвигатель устанавливается на салазки (рис. 8). Размеры и масса салазок пяти типоразмеров приведены в табл. 18.
Таблица 18 – Салазки для электродвигателя
| Тип | Размеры, мм | Масса комплекта, кг | Болты для крепления двигателя dxl, мм | ||||||||||

| 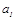
| 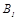
| 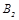
| 
| 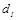
| 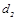
| 
| 
| 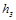
| 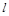
| |||
| С-3 | M12 | 3,8 | М10´35 | ||||||||||
| С-4 | М12 | 5,3 | М12´40 | ||||||||||
| С-5 | М16 | 12,5 | М16х55 | ||||||||||
| С-6 | М16 | 17,5 | М16´60 | ||||||||||
| С-7 | М20 | М20´75 |
В табл.18 также приведены диаметры и длины болтов для крепления электродвигателя к салазкам.
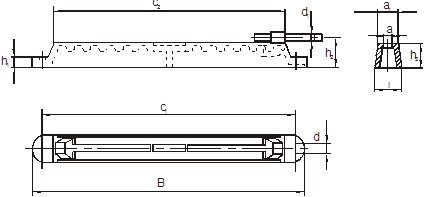
Рисунок 8 – Салазки для электродвигателя
2 Зубчатые передачи в закрытом исполнении
2.1 Теоретические предпосылки к расчетам
Для закрытых зубчатых передач возможны следующие критерии работоспособности:
усталостная контактная прочность зубьев;
усталостная изгибная прочность зубьев;
статическая изгибная прочность зубьев в условиях кратковременных перегрузок;
статическая контактная прочность зубьев в условиях кратковременных перегрузок.
Из названных критериев наиболее вероятный первый, по которому рекомендуется вести проектировочный расчет, однако в проверочном расчете проверяется работоспособность передачи по всем перечисленным критериям.
Контактная прочность зубчатого колеса при прочих равных условиях зависит только от его диаметра, поэтому из условия контактной прочности можно рассчитать размеры зубчатых колес или передачи. Изгибная прочность зависит от модуля.
При используемых для изготовления зубчатых колес материалах изгибную прочность зубьев часто можно обеспечить очень мелкими модулями.
Практически мелкомодульные  зубчатые колеса в редукторостроении для силовых передач не применяются, так как они очень чувствительны к износу, дефекту материала, перегрузкам. Сложен их контроль. Поэтому модуль обычно не рассчитывают, а назначают из стандартного ряда (ГОСТ 9563-60), используя одну из следующих рекомендаций.
зубчатые колеса в редукторостроении для силовых передач не применяются, так как они очень чувствительны к износу, дефекту материала, перегрузкам. Сложен их контроль. Поэтому модуль обычно не рассчитывают, а назначают из стандартного ряда (ГОСТ 9563-60), используя одну из следующих рекомендаций.
1 Примерное значение модуля в передаче стальными цилиндрическими колесами:  при
при  ;
; 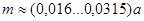 при
при 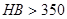 .
.
2 В редукторных передачах незакаленными цилиндрическими зубчатыми колесами 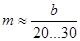 , закаленными цилиндрическими зубчатыми колесами -
, закаленными цилиндрическими зубчатыми колесами -  . В коробках скоростей -
. В коробках скоростей -  .
.
3 Желательно, чтобы модуль обеспечивал число зубьев шестерни не ниже минимально возможного из условия отсутствия подрезания. При  для прямозубых цилиндрических колес
для прямозубых цилиндрических колес 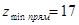 , при
, при 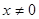 данные о минимально возможном числе зубьев без подреза дает табл. 22. Для косозубых -
данные о минимально возможном числе зубьев без подреза дает табл. 22. Для косозубых -  , для прямозубых конических -
, для прямозубых конических -  , для косозубых конических и колес с круговыми зубьями -
, для косозубых конических и колес с круговыми зубьями - 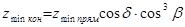 .
.
Лучше иметь на шестерне число зубьев на 3…5 больше от минимально возможного.
4 В передаче прямозубыми цилиндрическими зубчатыми колесами назначенный модуль должен обеспечивать условие
 - целое число,
- целое число,
в передаче косозубыми –
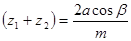 - целое число. После округления чисел зубьев до целого числа уточняется угол
- целое число. После округления чисел зубьев до целого числа уточняется угол 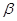 .
.
В случае неудовлетворительного результата проверочного расчета на изгибную прочность модуль должен быть увеличен.
5 При межосевом расстоянии, назначенном из условия контактной прочности зубьев, и модуле, назначенном по рекомендациям предыдущего пункта, числа зубьев находятся расчетом:
 - с округлением до ближайшего целого числа;
- с округлением до ближайшего целого числа;
 .
.
Фактическое передаточное число  может оказаться отличным от заданного, но процент ошибки не должен превышать 2,5% при
может оказаться отличным от заданного, но процент ошибки не должен превышать 2,5% при 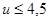 и 4% - при
и 4% - при  .
.
6 Расчеты цилиндрических зубчатых передач на контактную усталостную прочность основываются на следующем условии:
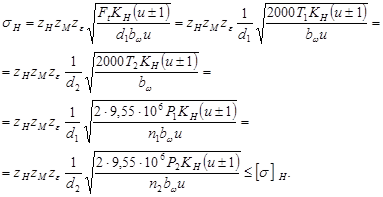 (14)
(14)
Заменяя 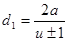 ;
; 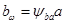 ;
; 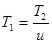 и решая относительно межосевого расстояния, можно получить:
и решая относительно межосевого расстояния, можно получить:
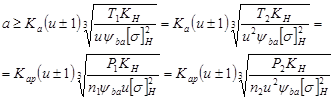 (15)
(15)
где 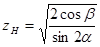 - коэффициент, учитывающий форму сопряженных поверхностей зубьев.
- коэффициент, учитывающий форму сопряженных поверхностей зубьев.
Для прямозубых колес при 
 .
.
Для косозубых – при  ;
; 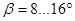
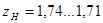 .
.
Для шевронных – при  ;
; 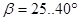 ,
,  .
.
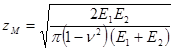 - коэффициент, учитывающий механические свойства материалов сопряженных зубчатых колес.
- коэффициент, учитывающий механические свойства материалов сопряженных зубчатых колес.
При модуле упругости:
стали - 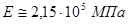 ;
;
чугуна -  ;
;
коэффициент Пуассона 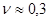 -
-
численные значения 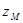 приведены в табл. 19.
приведены в табл. 19.
Таблица 19 - Значения 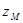
| Сочетание материалов | 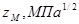
|
| Сталь-сталь | |
| Сталь-чугун |
 - коэффициент, учитывающий суммарную длину контактных линий,
- коэффициент, учитывающий суммарную длину контактных линий,
где  ,
, 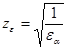 ,
,
где 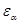 - торцевой коэффициент перекрытия,
- торцевой коэффициент перекрытия,
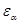
 . (16)
. (16)
Приближенные значения 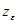 :
:
для прямозубых колес -  ;
;
для косозубых и шевронных колес -  .
.
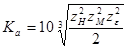 - средний суммарный коэффициент при расчетах межосевого расстояния с использованием момента.
- средний суммарный коэффициент при расчетах межосевого расстояния с использованием момента.
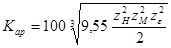 - средний суммарный коэффициент при расчетах межосевого расстояния с использованием мощности.
- средний суммарный коэффициент при расчетах межосевого расстояния с использованием мощности.
Значения коэффициентов  представлены в табл. 20.
представлены в табл. 20.
Таблица 20 - Значения средних суммарных коэффициентов 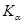 ,
, 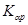
| Сочетание материалов | Вид передачи | 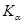 , , 
| 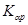 , , 
|
| Сталь-сталь | Прямозубая | 9,75×103 | |
| Косозубая | 8,9×103 | ||
| Шевронная | 8,7×103 | ||
| Сталь-чугун | Прямозубая | 7,85×103 | |
| Косозубая | 7,1×103 | ||
| Шевронная | 6,9×103 |
7 Из анализа коэффициентов, приведенных в табл. 20, следует, что для ориентировочного расчета зубчатых передач косозубыми и шевронными зубчатыми колесами могут быть использованы формулы для расчета передач прямозубыми колесами в предположении, что нагрузочная способность последних в среднем в 1,4 раза выше, чем прямозубых.
Повышенная нагрузочная способность косозубых и шевронных зубчатых колес связана с торцевым перекрытием зубьев (возможностью ввести в зацепление два и более зубьев), незначительным колебанием суммарной длины контактных линий и рядом других особенностей зацепления. Приведенная рекомендация справедлива при обычно принимаемых углах наклона зуба (косозубые -  ; шевронные -
; шевронные -  ) и торцевом перекрытии хотя бы одной пары зубьев, т.е. выполнении условия
) и торцевом перекрытии хотя бы одной пары зубьев, т.е. выполнении условия
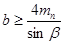 .
.
8 Передачи шевронными зубчатыми колесами при расчете можно рассматривать как две параллельно работающие косозубые передачи и вести расчет в предположении, что каждый полушеврон передает половину общей нагрузки.
Рассчитывая шевронные передачи по методу полушевронов, не следует забывать, что общая ширина шевронного колеса более чем в 2 раза шире полушеврона (за счет канавки между полушевронами для выхода режущего инструмента).
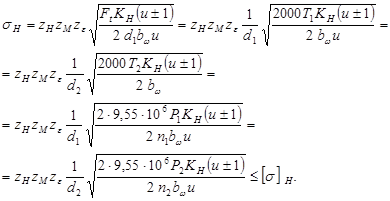 (17)
(17)
 (18)
(18)
9 Расчет конических зубчатых передач на контактную прочность основывается на следующем условии:
 (19)
(19)
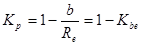 .
.
Если принять 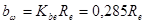 , а коэффициент
, а коэффициент 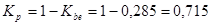 , можно получить:
, можно получить:
 , (20)
, (20)
где  (табл. 21);
(табл. 21);
 (см. табл. 21).
(см. табл. 21).
Таблица 21 - Значения 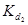 ,
, 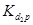
| Сочетание материалов | Вид передачи | 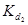 , , 
| 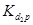 , , 
|
| Сталь-сталь | Прямозубая | 33×103 | |
| Косозубая | 30×103 | ||
| Сталь-чугун | Прямозубая | 27×103 | |
| Косозубая | 24,5×103 |
Ряд авторов, ссылаясь на опытные данные, рекомендует при использовании написанных теоретических формул завышать расчетную нагрузку в среднем на 20% 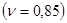 .
.
10 Из анализа коэффициентов, приведенных в табл. 21, следует, что для ориентировочных расчетов конических косозубых передач могут быть использованы формулы для расчетов передач прямозубыми зубчатыми колесами в предположении, что нагрузочная способность последних в среднем в 1,4 раза выше, чем прямозубых.
11 Расчеты прямозубых цилиндрических зубчатых передач на изгибную прочность основываются на следующем условии:
 . (21)
. (21)
Расчеты косозубых цилиндрических передач – на следующем условии:
 . (22)
. (22)
Расчеты шевронных цилиндрических передач – на следующем условии
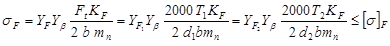 . (23)
. (23)
Расчеты прямозубых конических передач – на следующем условии:
 . (24)
. (24)
Расчеты косозубых конических передач – на следующем условии:
 , (25)
, (25)
где 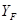 - безразмерный коэффициент, величина которого зависит от формы зуба (ширины основания, фактической высоты головки, ножки зуба, фактического угла зацепления, формы галтели).
- безразмерный коэффициент, величина которого зависит от формы зуба (ширины основания, фактической высоты головки, ножки зуба, фактического угла зацепления, формы галтели).
Значения этого коэффициента для зубчатых колес внешнего зацепления дает табл. 22 (выборка из ГОСТ 21354‑87).
Выбор 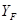 для косозубых зубчатых колес выполняется по эквивалентному числу зубьев
для косозубых зубчатых колес выполняется по эквивалентному числу зубьев  ; для прямозубых конических -
; для прямозубых конических -  ; для косозубых конических -
; для косозубых конических - 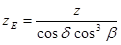 .
.
 - коэффициент, учитывающий наклон зуба.
- коэффициент, учитывающий наклон зуба.
С достаточной для практических расчетов точностью можно принимать:
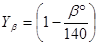 .
.
Таблица 22 - Значения коэффициента 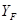
 или или 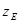
| Коэффициент смещения 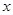
| ||||||||
| -0,5 | -0,4 | -0,25 | -0,16 | +0,16 | +0,25 | +0,4 | +0,5 | ||
| - | - | - | - | - | - | - | 3,58 | 3,47 | |
| - | - | - | - | - | 4,04 | 4,00 | 3,55 | 3,42 | |
| - | - | - | - | 4,28 | 4,02 | 3,78 | 3,54 | 3,40 | |
| - | - | - | 4,40 | 4,09 | 3,83 | 3,64 | 3,50 | 3,39 | |
| - | - | 4,30 | 4,14 | 3,90 | 3,72 | 3,62 | 3,47 | 3,40 | |
| 4,6 | 4,3 | 4,05 | 3,95 | 3,80 | 3,67 | 3,6 | 3,48 | 3,45 | |
| 4,14 | 4,02 | 3,88 | 3,81 | 3,70 | 3,61 | 3,57 | 3,48 | 3,42 | |
| 3,96 | 3,88 | 3,78 | 3,73 | 3,65 | 3,58 | 3,54 | 3,49 | 3,44 | |
| 3,83 | 3,80 | 3,73 | 3,70 | 3,62 | 3,60 | 3,55 | 3,53 | 3,49 | |
| 3,73 | 3,70 | 3,66 | 3,63 | 3,61 | 3,55 | 3,54 | 3,51 | 3,50 | |
| 100 и более | 3,68 | 3,66 | 3,62 | 3,61 | 3,60 | 3,56 | 3,56 | 3,55 | 3,52 |
Заменяя 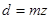 ,
,  ,
,  , можно получить:
, можно получить:
для прямозубых цилиндрических зубчатых колес –
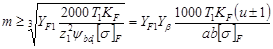 ; (26)
; (26)
для косозубых зубчатых колес –
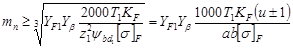 ; (27)
; (27)
для шевронных зубчатых колес –
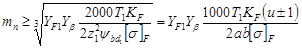 ; (28)
; (28)
для конических прямозубых зубчатых колес –
 ; 29)
; 29)
для конических косозубых зубчатых колес –
 . (30)
. (30)
Расчеты зубчатых передач на прочность (контактную и изгибную) при действии кратковременной максимальной нагрузки основываются на следующем условии:
 ;
;  , (31)
, (31)
где  - коэффициент перегрузки, определяется либо нагрузочной способностью электродвигателя:
- коэффициент перегрузки, определяется либо нагрузочной способностью электродвигателя:
 , (32)
, (32)
либо при наличии в конструкции привода фрикционной муфты (сцепной или предохранительной) определяется коэффициентом запаса сцепления 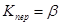 , который указан в исходных данных на проектирование.
, который указан в исходных данных на проектирование.
Расчеты выполняются для шестерни и колеса раздельно или только для одного из зубчатых колес пары, если заведомо известен “слабый” элемент.
12 Особенности расчета передач, зубчатые колеса которых нарезаны со смещением инструмента.
Следует различать два типа передач со смещением.
Шестерня изготовлена с положительным смещением 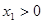 , колесо – с отрицательным
, колесо – с отрицательным  , но так, что
, но так, что  , или
, или  .
.
Так как в этом случае начальные окружности совпадают с делительными и угол зацепления не меняется, расчет на контактную прочность выполняется так же, как для передач без смещения. Изменение формы зуба учитывается только в расчетах на изгибную прочность выбором коэффициента 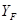 с учетом величины смещения (см. табл. 22).
с учетом величины смещения (см. табл. 22).
Суммарное смещение  . В этом случае начальные окружности не совпадают с делительными и угол зацепления
. В этом случае начальные окружности не совпадают с делительными и угол зацепления  отличен от
отличен от  .
.
При выполнении расчетов на контактную прочность в соответствующих формулах под межосевым расстоянием следует понимать начальное межосевое расстояние  , под диаметрами зубчатых колес – начальные диаметры
, под диаметрами зубчатых колес – начальные диаметры 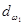 ,
, 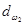 :
:
 ;
; 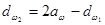 ;
;
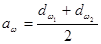 .
.
Коэффициент 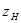 необходимо рассчитывать с учетом действительного угла зацепления
необходимо рассчитывать с учетом действительного угла зацепления  .
.
Назначенный модуль должен отвечать условию:
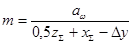 ,
,
где  ;
; 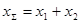 ;
; 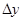 - коэффициент уравнительного смещения по ГОСТ 16532-70 (при
- коэффициент уравнительного смещения по ГОСТ 16532-70 (при 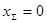
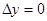 ).
).
В расчетах на изгибную прочность коэффициент 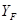 выбирается с учетом величины смещения.
выбирается с учетом величины смещения.
В зубчатых колесах, вырезанных со смещением, диаметр вершин зубьев рассчитываем по формуле:
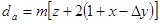 .
.
13 В зацеплении прямозубых цилиндрических зубчатых колес возникают две силы– окружная  и радиальная
и радиальная 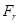 .
.
 ;
;
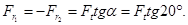
В зацеплении косозубых цилиндрических зубчатых колес – три силы: окружная  , радиальная
, радиальная 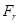 и осевая
и осевая 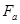 .
.
 ;
;
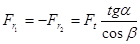 ;
;
 .
.
14 В зацеплении прямозубых конических зубчатых колес – три силы: окружная  , радиальная
, радиальная 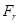 и осевая
и осевая 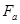 .
.
Окружная сила на среднем диаметре
 ,
,
где  - окружная сила на внешнем диаметре делительного конуса;
- окружная сила на внешнем диаметре делительного конуса;
 средний диаметр и окружная скорость на среднем диаметре конического колеса.
средний диаметр и окружная скорость на среднем диаметре конического колеса.
 ;
;
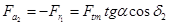 .
.
Осевая сила всегда направлена к основанию конуса. В зацеплении косозубых конических и конических с круговым зубом зубчатых колес тоже возникают три силы: окружная  , радиальная
, радиальная 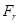 и осевая
и осевая 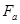 , причем направление двух последних зависит от направления зуба и направления вращения зубчатого колеса.
, причем направление двух последних зависит от направления зуба и направления вращения зубчатого колеса.
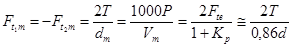 ;
;
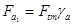 ;
;
 ;
;
 ;
;
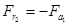 .
.
Формулы для определения коэффициентов  и
и  приведены в табл. 23.
приведены в табл. 23.
Таблица 23 - Силы в зацеплении конических передач
| Схема шестерни | 
| 
| |

| Направление зуба правое, вращение по часовой стрелке | 
| 
|

| Направление зуба левое, вращение против часовой стрелки | ||

| Направление зуба правое, вращение против часовой стрелки | 
| 
|

| Направление зуба левое, вращение по часовой стрелке |
Направление зуба шестерни в редуцирующей передаче следует выбирать таким, чтобы сила 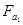 была направлена к основанию конуса, что соответствует условию: направление вращения шестерни (со стороны вершины делительного конуса) должно быть таким же, как направление ее зуба. Направление зуба сопряженного колеса обратно направлению зуба шестерни.
была направлена к основанию конуса, что соответствует условию: направление вращения шестерни (со стороны вершины делительного конуса) должно быть таким же, как направление ее зуба. Направление зуба сопряженного колеса обратно направлению зуба шестерни.
2.2 Рекомендуемый порядок расчета передач в закрытом исполнении
2.2.1 Передачи цилиндрическими зубчатыми колесами
2.2.1.1 Исходные данные
Для выполнения расчета передачи необходимо иметь следующие данные: 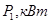 ;
; 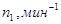 (
(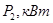 ,
, 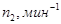 ) или
) или 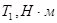 (
(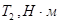 ),
), 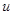 , режим нагружения (см. результаты кинематического расчета и данные бланка задания).
, режим нагружения (см. результаты кинематического расчета и данные бланка задания).
Режим нагружения передачи связан с эксплуатационными особенностями машины, которую обслуживает привод. Он включает следующие сведения: общий срок службы  , который разбит на составляющие
, который разбит на составляющие 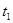 ,
, 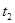 ,
,  … по принципу примерно одинаковой нагрузки; величину нагрузки в пределах каждой составляющей
… по принципу примерно одинаковой нагрузки; величину нагрузки в пределах каждой составляющей  ,
, 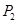 ,
, 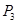 …; частоту вращения
…; частоту вращения 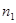 ,
, 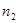 ,
, 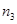 … Данные должны позволять рассчитывать число циклов перемен напряжений в зубе зубчатого колеса на каждом частном режиме нагружения.
… Данные должны позволять рассчитывать число циклов перемен напряжений в зубе зубчатого колеса на каждом частном режиме нагружения.
2.2.1.2 Проектировочный расчет
Рекомендуется вести в следующей последовательности:
1 Назначить материалы зубчатых колес пары, рассчитать контактные допускаемые напряжения.
Основным материалом для изготовления зубчатых колес является сталь, а способ получения заготовки – ковка, штамповка. Стальное литье обладает пониженной прочностью и используется для колес особо крупных размеров.
Чугун применяют для изготовления крупногабаритных тихоходных колес. Из пластмасс (текстолит, полиамиды) обычно изготовляется одно из колес пары в малонагруженных и кинематических передачах с целью обеспечить бесшумную работу.
Так как контактная прочность зубьев зависит, в основном, от поверхностной твердости, все более широкое распространение получают всевозможные методы термической и термохимической обработки стальных зубчатых колес: термическое улучшение, закалка, цементация, азотирование, цианирование.
Термическая и термохимическая обработка позволяет существенно уменьшить габариты передачи, однако требует специального оборудования, поэтому получила распространение в машинах серийного и массового производства. В машинах индивидуального и мелкосерийного производства применяется ограниченно.
С целью создания относительной равнопрочности шестерни и колеса, а также направленного истирания, рекомендуется выбирать материал или термообработку шестерни так, чтобы твердость ее была на 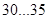 единиц
единиц 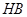 больше твердости сопряженного колеса. С наклонным расположением контактной линии связана целесообразность изготовления косозубой шестерни из материала, значительно более прочного (высокотвердого), чем у колеса. Поэтому для косозубых и шевронных передач необходимо стараться иметь колесо менее твердое, чем шестерня на 100 ед. НВ. Это объясняется следующим. Ножки зубьев обладают меньшей стойкостью против выкрашивания, чем головки, так как у них неблагоприятно сочетание направления скольжения и перекатывания зубьев. Следовательно, ножка зуба колеса, работающая с головкой зуба шестерни начнет выкрашиваться в первую очередь. Вследствие наклона контактной линии нагрузка (полностью или частично) передается на головку зуба колеса, работающую с ножкой зуба шестерни. Дополнительная нагрузка ножки зуба шестерни не опасна, так как она изготовлена из более стойкого материала. Применение твердой шестерни позволяет дополнительно повысить нагрузочную способность косозубых передач на 25-30%.
больше твердости сопряженного колеса. С наклонным расположением контактной линии связана целесообразность изготовления косозубой шестерни из материала, значительно более прочного (высокотвердого), чем у колеса. Поэтому для косозубых и шевронных передач необходимо стараться иметь колесо менее твердое, чем шестерня на 100 ед. НВ. Это объясняется следующим. Ножки зубьев обладают меньшей стойкостью против выкрашивания, чем головки, так как у них неблагоприятно сочетание направления скольжения и перекатывания зубьев. Следовательно, ножка зуба колеса, работающая с головкой зуба шестерни начнет выкрашиваться в первую очередь. Вследствие наклона контактной линии нагрузка (полностью или частично) передается на головку зуба колеса, работающую с ножкой зуба шестерни. Дополнительная нагрузка ножки зуба шестерни не опасна, так как она изготовлена из более стойкого материала. Применение твердой шестерни позволяет дополнительно повысить нагрузочную способность косозубых передач на 25-30%.
В табл. 24 приведены материалы, наиболее часто применяемые для изготовления зубчатых колес относительно небольшого размера, и некоторые их характеристики. В табл. 25 приведены рекомендации к выбору вариантов материалов шестерни и колеса.
| Таблица 24 - Некоторые материалы для изготовления зубчатых колес и их характеристики | 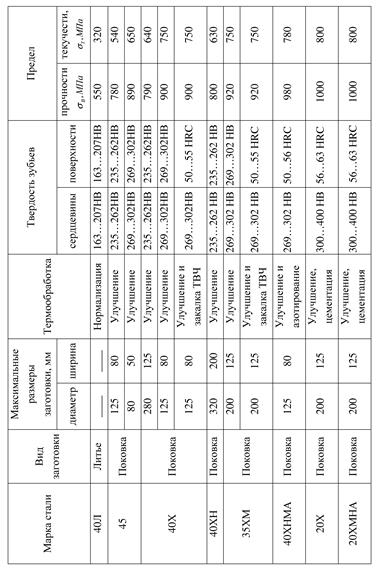
|
Таблица 25 – Рекомендации к выбору материалов для шестерни и колеса
| Варианты | Шестерня | Колесо | ||||
| Марка стали | Термообработка | Твердость | Марка стали | Термообработка | Твердость | |
| 40Х,45, 40ХН | Улучшение | 269... 302НВ | 40Х,45, 40ХН | Улучшение | 235... 262 НВ | |
| 40Х, 40ХН, 35ХМ | Улучшение и закалка ТВЧ | 50...55 HRC | 40Х, 40ХН, 35ХМ | Улучшение | 269... 302 НВ | |
| 40Х, 40ХН, 35ХМ | Улучшение и закалка ТВЧ | 50...55 HRC | 40Х, 40ХН, 35ХМ | Улучшение и закалка ТВЧ | 50...55 HRC | |
| 20Х, 20ХНМ | Улучшение, цементация, закалка | 57...63 HRC | 40Х, 40ХН, 35ХМ | Улучшение и закалка ТВЧ | 50...55 HRC | |
| 20Х, 20ХНМ | Улучшение, цементация, закалка | 57...63 HRC | 20Х, 20ХНМ | Улучшение, цементация, закалка | 57...63 HRC |
Пользуясь данными табл. 24, следует иметь в виду, что возможность получения той или иной твердости заготовки (зубчатого колеса) при термической обработке зависит от ее размера или формы. Наибольшую твердость можно получить только при малых диаметрах (до 100…120 мм) или малых толщинах сечений (до 40…60 мм). Численные значения пределов текучести и прочности, указанные в табл. 24, следует рассматривать как некоторые средние. При отсутствии более точных данных в практике иногда пользуются следующими приближенными расчетами:
Углеродистые стали:
нормализация -  ;
; 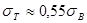 ;
;
улучшение -  ;
; 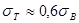 .
.
Легированные стали:
улучшение -  ;
; 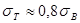 .
.
Допускаемые контактные напряжения для цилиндрических передач определяют по формуле:
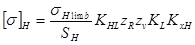 ,
,
где 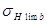 - предел контактной выносливости, соответствующий базовому числу циклов
- предел контактной выносливости, соответствующий базовому числу циклов 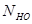 ;
;
 - коэффициент безопасности;
- коэффициент безопасности;
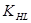 - коэффициент долговечности;
- коэффициент долговечности;
 - коэффициент, учитывающий шероховатость сопряженных поверхностей;
- коэффициент, учитывающий шероховатость сопряженных поверхностей;
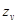 - коэффициент, учитывающий влияние окружной скорости;
- коэффициент, учитывающий влияние окружной скорости;
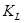 - коэффициент, учитывающий влияние смазки;
- коэффициент, учитывающий влияние смазки;
 - коэффициент, учитывающий влияние размера колеса.
- коэффициент, учитывающий влияние размера колеса.
При одинаковой твердости зубьев шестерни и колеса расчет ведется по шестерне.
Для прямозубых и косозубых передач с твердостью зубьев 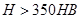 в качестве расчетного допускаемого напряжения
в качестве расчетного допускаемого напряжения 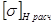 принимается меньшее из двух допускаемых напряжений, определенных по материалу шестерни
принимается меньшее из двух допускаемых напряжений, определенных по материалу шестерни  и колеса
и колеса 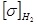 .
.
|
|
|
|
|
Дата добавления: 2015-04-24; Просмотров: 1005; Нарушение авторских прав?; Мы поможем в написании вашей работы!