В расчетах зубьев на контактную усталостную прочность допускается иметь расчетное контактное напряжение в пределах . 1 страница

Если за один оборот каждый зуб зубчатого колеса входит в зацепление два или несколько раз, следует в расчетные формулы подставлять в соответствующее число раз увеличенную частоту вращения.

Коэффициент долговечности имеет пределы возможных значений. Для материалов с однородной структурой (стали нормализованные, улучшенные, закаленные)

.

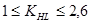Для материалов, поверхностно упрочненных (поверхностная закалка, цементация, нитроцементация, азотирование),

.

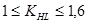Если расчетные значения 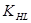выходят за пределы указанных предельных, их надо принимать предельными.

Коэффициент принимают по тому из зубчатых колес пары, которое имеет более грубую поверхность:

при 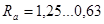(7-й класс) - ;

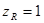при 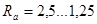(6-й класс) - ;

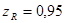при 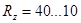(5-й класс) - .

Коэффициент 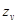приближенно может приниматься по следующим рекомендациям:

при 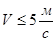во всех случаях - ;

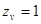при 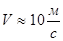и прирабатывающихся зубьях ;

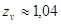при 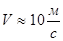и не прирабатывающихся зубьях - ;

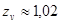при 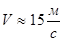и прирабатывающихся зубьях - ;

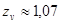при 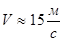и не прирабатывающихся зубьях - .

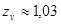Коэффициент 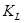для закрытых, обильно смазываемых передач следует принимать: .

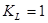Коэффициент при 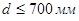принимают: 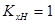, при больших диаметрах рассчитывают по формуле

.

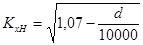2 Назначить коэффициенты , .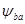

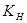При расчетах косозубых и шевронных передач дополнительно назначается ориентировочный угол наклона зуба .

Коэффициент ширины зубчатого колеса относительно межосевого расстояния 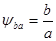назначается из ряда по ГОСТ2185-66 (табл. 28).

Таблица 28 - Коэффициенты ширины зубчатого венца

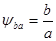
	0,100	0,125	0,160	0,200	0,250	0,315	0,400	0,500
0,630	0,800	1,000	1,250

При назначении коэффициента 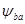могут быть использованы следующие рекомендации:

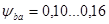- прямозубые зубчатые колеса, перемещающиеся на валах в осевом направлении (блочные);

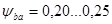- прямозубые зубчатые колеса на длинных нежестких валах (коробки скоростей);

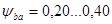- прямозубые зубчатые колеса на недлинных жестких валах (многоступенчатые редукторы);

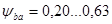- косозубые зубчатые колеса на недлинных жестких валах, причем тем больше, чем меньше угол наклона зуба, и наоборот (условие 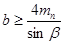ориентировочно обеспечивается при 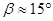и );

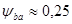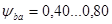- шевронные зубчатые колеса, прямозубые и косозубые зубчатые колеса на коротких жестких валах (одноступенчатые редукторы);

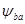до 1,25 - тяжелые одноступенчатые редукторы.

Если хотя бы одно из зубчатых колес пары укреплено на консоли вала, значения 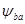выбирают как можно меньше. В многоступенчатых редукторах значения 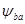увеличиваются в направлении от быстроходной к тихоходной передаче. Повышение точности изготовления и монтажа передачи, повышение жесткости валов позволяет принимать более высокое значение .

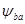Выбранный коэффициент 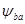в конечном счете определяет ширину зубчатых колес. Считается удачной конструкция, у которой:

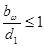- прямозубые колеса;

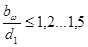- косозубые колеса;

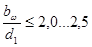- шевронные колеса.

Коэффициент 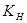в общем случае равен:

,

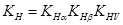где 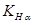- коэффициент, учитывающий распределение нагрузки между зубьями.

Для прямозубых передач принимается .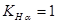

Для косозубых и шевронных передач назначение этого коэффициента связывают с окружной скоростью и степенью точности зубчатых колес. Имея в виду, что окружная скорость определенным образом связана со степенью точности, в конкретных расчетах можно пользоваться рекомендациями табл.29.

Таблица 29 - Коэффициент 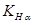для косозубых и шевронных передач

Окружная скорость	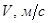Значения коэффициента 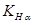для степени точности по нормам плавности
2,5		1,01	1,03	1,05	1,13
		1,02	1,05	1,09	1,16
	1,01	1,03	1,07	1,13	---
	1,01	1,04	1,09	---	---
	1,02	1,05	1,12	---	---
	1,02	1,06	---	---	---

В проектировочном расчете целесообразно принимать .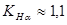

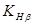- коэффициент, учитывающий распределение нагрузки по ширине венца.

При расчетах на контактную прочность 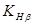в реальных передачах имеет значения в пределах:

прирабатывающиеся зубчатые колеса (твердость хотя бы одного колеса ) - ;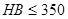

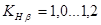не прирабатывающиеся зубчатые колеса - .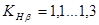

В проектировочном расчете им можно просто задаться. Относительно точные значения 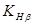дает табл. 35. При пользовании таблицей следует иметь в виду, что

.

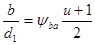- коэффициент динамичности нагрузки. Может быть рассчитан только при известных размерах передачи, поэтому в проектировочном расчете либо принимают 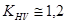, либо ориентируются на следующие возможные значения:

прирабатывающиеся зубчатые колеса - ;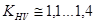

не прирабатывающиеся зубчатые колеса - .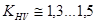

В передачах косозубыми и шевронными зубчатыми колесами коэффициент меньше, чем в передачах прямозубыми колесами.

Практически углы наклона зубьев назначаются в пределах:

косозубые зубчатые колеса - ;

шевронные зубчатые колеса - .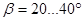

3 Из условия контактной прочности рассчитать и назначить межосевое расстояние.

Независимо от того, ведется расчет по шестерни или колесу, в качестве 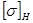выбирается меньшее из двух , 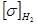(или 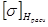при расчетах передач косозубыми зубчатыми колесами со значительной разницей твердости).

Рассчитанное значение межосевого расстояния округляется до стандартного (табл. 30).

Таблица 30 - Межосевое расстояние 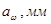, по ГОСТ 2185-66

1-й ряд							-		-
2-й ряд	-	-				-		-		-

1-й ряд	-		-		-		-		-
2-й ряд		-		-		-		-		-

1-й ряд	-		-		-		-		-
2-й ряд		-		-		-		-

Примечание. Первый ряд предпочитать второму.

4 Назначить модуль.

Назначенный модуль должен быть принят из ряда значений по ГОСТ 9563-60.

Таблица 31 - Модули 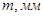, в наиболее употребительном диапазоне

1-й ряд		1,25	1,5		2,5
2-й ряд	1,125	1,375	1,75	2,25	2,75	3,5	4,5	5,5

Примечание. Первый ряд предпочитать второму.

Минимально возможный модуль можно рассчитать из условия усталостной изгибной прочности по приведенным выше формулам. Однако, как отмечалось, практически его назначают большим, преследуя цель обеспечить выполнение некоторых вспомогательных условий: целое число суммы зубьев при назначенном стандартном межосевом расстоянии, возможность контроля точности универсальным инструментом и т.п.

Вместе с тем не следует чрезмерно завышать модуль, т.к. при меньшем модуле выше плавность хода передачи, меньше потери на трение, меньше наружный диаметр зубчатых колес и уменьшается расход металла на их изготовление, уменьшается объем срезаемого при изготовлении зубчатого колеса материала, т.е. меньше стоимость зубонарезания. Для силовых передач рекомендуется .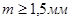

5 Рассчитать числа зубьев зубчатых колес пары.

Следует иметь в виду, что в формуле для определения суммы зубьев передачи косозубыми зубчатыми колесами стоит косинус угла наклона зуба:

.

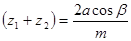Практически поступают так. Сначала задаются желаемым ориентировочным углом наклона , затем рассчитывают значение суммы зубьев и округляют ее до ближайшего целого числа, а потом при этом принятом целом числе уточняют действительный угол наклона по формуле 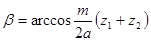с точностью до четвертого знака после запятой.

6 Рассчитать геометрические размеры шестерни и колеса.

6.1 Ширина колеса

.

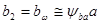Знак приближения в формуле указывает на необходимость рассчитанное значение округлить до ближайшего размера по ГОСТ 6636-69 не ниже ряда 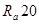(табл. 32).

Таблица 32 - Нормальные линейные размеры (из ГОСТ 6639-69)

	2,5	4,0	6,3	10,0
	2,5	3,2	4,0	5,0	6,3	8,0	10,0	12,0
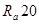
	2,5	2,8	3,2	3,6	4,0	4,5	5,0	5,6	6,3	7,1

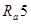
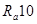
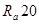
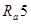
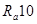
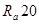
Продолжение таблицы 32

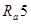
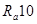
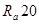
Ширина шестерни 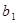принимается несколько большей ширины колеса: 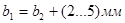для компенсации неточностей монтажа.

6.2 Диаметры зубчатых колес:

прямозубых –

;

;

;

;

;

;

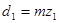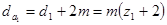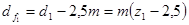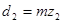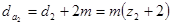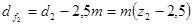косозубых –

;

;

;

;

;

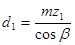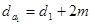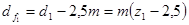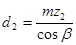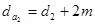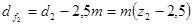
с точностью до четвертого знака после запятой.

7 Точность зубчатых колес

Одним из основных показателей качества зубчатых колес является их точность. Точность изготовления зубчатых колес и передач определяет не только их кинематические и эксплуатационные показатели, а и такие характеристики как интенсивность шума и вибрации, а также существенно влияет на показатели прочности передачи, долговечность ее работы, потери на трение и т.д. Основными показателями точности функционирования эвольвентных зубчатых передач являются: кинематическая точность, плавность работы, контакт зубьев, боковой зазор.

По нормам кинематической точности, плавности работы и контакта зубьев зубчатые передачи делят на 12 ступеней точности. Основанием для назначения степени точности зубчатых колес рассчитываемой передачи является окружная скорость

.

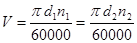Рекомендованные степени точности зубчатых передач в зависимости от окружной скорости для силовых передач приведены в табл.33.

При одинаковой степени точности по всем нормам условное обозначение состоит из цифры и буквы, которые разделены тире. Цифра означает степень точности, а буква – вид сопряжения зубьев, например: 9 – В ГОСТ 1643- 81 – для цилиндрической эвольвентной передачи.

Видом сопряжения и видом допуска устанавливается боковой зазор в передаче. Для зубчатых передач с модулем 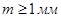установлено шесть видов сопряжения: А, В, С, Д, Е, Н и восемь видов допуска на боковой зазор: x, y, z, a, b, c, d, h. В большинстве случаев для силовых передач рекомендуется использовать сопряжение вида В, а для реверсивных передач - сопряжение вида С и Д.

Таблица 33 - Рекомендации к выбору степени точности зубчатых передач в зависимости от окружной скорости, м/с

Степень кинематической точности	Прямые зубья для передачи	Непрямые зубья для передачи	Область использования
цилиндрической	конической	цилиндрической	конической
	³ 15	³ 12	³ 30	³ 20	Высокоскоростные передачи в авиамашиностроении, делительные механизмы
	До 15	До 12	До 30	До 20
	До 10	До 8	До 15	До 10	Передачи общего назначения
	До 6	До 4	До 10	До 7
	До 2	До 1,5	До 3	До 2	Тихоходные передачи сельскохозяйственных машин

Практически редко встречаются передачи, в которых для обеспечения качества все три вида норм необходимо выдерживать с одинаковой степенью точности. В большинстве случаев один или два показателя точности являются определяющими, а другие менее важные. В зависимости от конкретных эксплуатационных требований к зубчатой передаче рекомендуются следующие комбинации степеней точности (при 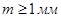) в зависимости от кинематической точности (номера степени точности) (табл. 34).

Таблица 34 - Рекомендуемые комбинации степеней точности зубчатых передач

Показатели точности	Условия эксплуатации
Для особенно точных делительных механизмов и механизмов отсчета	Для высокоскоростных передач	Для передач общего назначения	Для силовых передач
Плавность работы	-2	-1		+1
Контакт зубьев	£ ( -2)	£ ( -1)	£	£( +1)

При комбинировании норм с разными ступенями точности в условном обозначении последовательно указывают через тире три цифры, которые соответственно означают степень точности по нормам кинематической точности, плавности работы и контакта зубьев, а буква – вид сопряжения зубьев: 8-7-6-Д ГОСТ 1758-81.

2.2.1.3 Проверочный расчет

Преследует цель проверить работоспособность передачи по всем возможным критериям работоспособности. Неудовлетворительные результаты хотя бы одной проверки требуют изменения параметров передачи.

Применительно к цилиндрическим зубчатым передачам в закрытом (редукторном) исполнении выполняют, обычно, следующие проверочные расчеты.

1 Проверка контактной выносливости зубьев.

Расчетное условие - .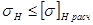

Расчетное контактное напряжение в полюсе зацепления при номинальной нагрузке может быть определено по ранее приведенным формулам (14),(17),(19).

Известные параметры передачи позволяют уточненно выбрать или рассчитать значения всех коэффициентов. При этом могут быть использованы рекомендации, приведенные выше, а также следующие сведения для уточненного назначения коэффициентов 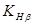, , 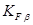, 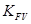(табл. 35,36).

Таблица 35 - Коэффициент распределения нагрузки по ширине колеса 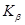(при расчетах на контактную прочность - 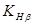, на изгибную прочность - )

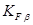	Положение зубчатого колеса относительно опор
в середине между опорами	вблизи одной из опор	на консоли
прирабат.	неприраб.	прирабат.	неприраб.	прирабат.	неприраб.
0,2						1,05	1,05	1,1	1,05	1,15	1,15	1,25
0,4				1,05	1,05	1,1	1,1	1,2	1,15	1,3	1,35	1,6
0,6		1,05	1,05	1,07	1,07	1,15	1,2	1,3	1,25	1,5	1,5	1,8
0,8		1,07	1,07	1,1	1,1	1,25	1,25	1,45	1,35	1,7	-	-
1,0	1,05	1,1	1,1	1,15	1,15	1,3	1,35	1,55	-	-	-	-
1,2	1,05	1,15	1,15	1,25	1,2	1,4	1,45	1,7	-	-	-	-

Таблица 36 - Коэффициенты динамического нагружения зубьев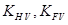

Дата добавления: 2015-04-24