Примеры. 1) . Операция сложения коммутативна и ассоциативна

1) 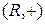. Операция сложения коммутативна и ассоциативна.

2) 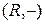. Операция вычитания не коммутативна и не ассоциативна. Например, , .

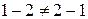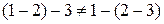3) 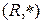, где 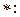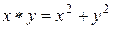. Такая операция 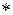коммутативна, но не ассоциативна. Действительно: .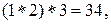

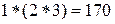4) Умножение матриц: ассоциативная, но не коммутативная операция.

Теорема 1 (обобщённая ассоциативность). Если операция 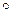ассоциативна, то в выражении 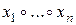скобки можно расставлять в любых местах.

Доказательство. Проводится методом математической индукции. Для 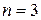утверждение повторяет определение ассоциативности. Пусть 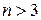. Рассмотрим выражения

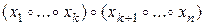и .

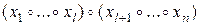Пусть 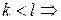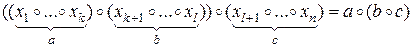− обычная ассоциативность. ■

Определение 4. Элемент 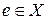называется нейтральным относительно алгебраической операции 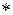, если

.

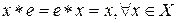(1)

Теорема 2. Нейтральный элемент единственен.

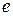Доказательство. (от противного). Пусть и ­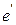− два нейтральных элемента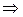

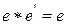(по условию нейтральност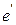и ) и

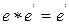(по условию нейтральности )

.■

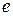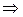
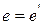Определение 5. Множество 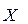с заданной на нем бинарной ассоциативной операцией называется полугруппой. Полугруппа с нейтральным элементом называется моноидом или полугруппой с единицей.

Определение 6. Элемент 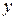моноида 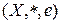называется симметричным к элементу 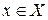, если

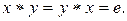
(2)

Теорема 3. Если в моноиде для 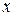есть симметричный элемент, то такой элемент единственен.

Доказательство. Пусть для данного 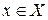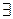два симметричных элемента 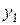и 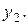Тогда в силу (1) и (2) имеем:

.■

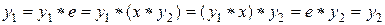Обычно умножение называют мультипликативной операцией, сложение – аддитивной. В случае мультипликативной операции результат операции 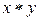называют произведением, нейтральный элемент – единицей (обозначают 1), симметричный элемент к 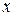– обратным (пишут 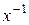). В случае аддитивной операции результат операции 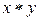называют суммой (x+y), нейтральный – нулём (обозначают 0), симметричный – противоположным (обозначают ).

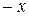Теорема 4. Если в моноиде 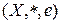для элементов 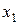и 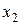есть симметричные элементы 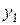и 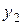соответственно, то для элемента 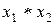также существует симметричный элемент, равный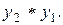

Доказательство. Для доказательства теоремы необходимо проверить условия (2): 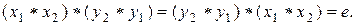Проверим первое из этих равенств. Имеем:

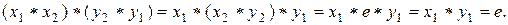
Аналогично проверяется второе условие из (2).■

2°.Группа, свойства группы.

Определение 7. Непустое множество G с заданной алгебраической операцией 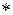называется группой, если

1) 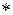– ассоциативная операция.

2) В G 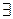нейтральный элемент .

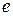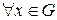
3) 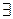симметричный элемент из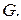

Если 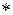– коммутативная операция, то группа называется коммутативной или абелевой.

Операция, относительно которой G − группа, называется групповой операцией. Если групповая операция 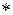− умножение, то группа называется мультипликативной, если 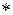– сложение, то G – аддитивная группа.

Примеры.

(N,+) ­ – коммутативная полугруппа без нейтрального элемента.

(N, 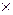) ­ – коммутативная полугруппа с нейтральным элементом.

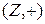– аддитивная абелева группа.

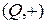– аддитивная абелева группа.

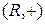– аддитивная абелева группа.

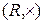– абелева полугруппа с нейтральным элементом.

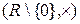– мультипликативная абелева группа.

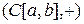– абелева группа: .

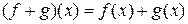Множество векторов на плоскости или в пространстве относительно операции сложения.

Дата добавления: 2015-04-25