Операции над множествами. Множеством принято называть вполне определенную со­вокупность предметов (объектов), которые являются элемен­тами множества

Понятие множества

Множеством принято называть вполне определенную со­вокупность предметов (объектов), которые являются элемен­тами множества. Рассматриваемое понятие (как и понятие фун­кции) лежит в основе всех разделов математики.

Примером множества могут служить следующие явления из области права:

множество правовых норм;

множествоорганов государства;

множество отраслей права;

множество компьютеров, установленных в данной орга­низации;

множество отпечатков пальцев в криминалистике;

множество субъектов федерации;

множество версий при расследовании преступления и т. д.

Множество, все элементы которого изолированы друг от друга, называется дискретным. Для измерения степени их изолированности вводится понятие расстояния между элемен­тами.

Всякое дискретное множество счетно, т. е. его элементы можно пронумеровать целыми числами.

Понятие дискретного множества чрезвычайно важно для информатики, поскольку лежит в основе разделения всех ус­тройств и систем обработки информации на два базовых клас­са — дискретные (цифровые) и непрерывные (аналоговые).*

* Типичный пример дискретного устройства — ЭВМ, состояние памяти которой представляется последовательностью двоичных цифр.

Подобно тому как из двух произвольных чисел с помощью арифметических операций можно получить некоторое другое число, из двух множеств можно сконструировать некоторое другое множество.

Существуют следующие операции над множествами: объе­динение (образование суммы) и пересечение. Для обозначения этих операций вводятся символы:

È (объединение), Ç (пересечение).

Объединением (суммой) двух множеств А и В называется множество А È В всех элементов, принадлежащих или мно­жеству А, или множеству В, или обоим сразу.

Пересечением двух множеств А и В называется множе­ство А Ç В всех элементов, принадлежащих множеству А и множеству В.

Таким образом:

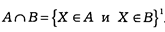
¹ Символ Î означает операцию включения Х в состав другого множества.

Дата добавления: 2015-04-25