Случайные величины и законы их распределения

Дальнейшим обобщением понятия случайного события является понятие случайной величины.

Случайной называется величина, которая в результате опыта (эксперимента, наблюдения, испытания) может принять то или иное значение, но неизвестно — какое именно.

Примеры случайных величин:

1) появление герба при трех бросаниях монеты (значения: 0, 1, 2, 3);

2) частота появления герба в том же опыте;

3) число отказавших элементов в приборе, состоящем из пяти элементов (возможные значения: 0, 1, 2, 3, 4, 5,...);

4) число попаданий в самолет, достаточных для выведе­ния его из строя;

5) число самолетов, сбитых в воздушном бою: I, 2, 3,... N, где N — число самолетов;

6) число совершенных преступлений в определенной мест­ности.

Закон распределения случайной величины — это всякое соотношение, устанавливающее связь между возможными зна­чениями случайной величины и соответствующими вероятнос­тями. Про случайную величину говорят; что она подчиняется данному закону распределения.

Случайные величины характеризуются двумя главными параметрами: математическим ожиданием и дисперсией.

Математическое ожидание есть теоретически возможное значение средней величины признака. Дисперсия — мера рас­сеяния случайной величины вокруг ее среднего значения.

Очень часто в качестве теоретической формулы распре­деления, описывающей социальные явления, используют фор­мулу нормального распределения признаков. В 1775 г. А. Муавр открыл закон распределения вероятностей, названный законом нормального распределения.

А. Кетле использовал нормальное распределение для изу­чения распределения людей по росту. Ф. Гальтон привлек нор­мальную кривую для статистического изучения законов, уп­равляющих наследственностью, К. Пирсон рассматривал нор­мальную кривую как основу биометрических измерений и по­строений и т. д. Разработка относящихся к этому закону вопро­сов связана с именами К. Гаусса и П. Лапласа.

Закон нормального распределения (часто называемый за­коном Гаусса, или нормальным законом) играет исключитель­ную роль в теории вероятностей и математической статистике и занимает среди других законов распределения особое место. Это — наиболее часто встречающийся на практике закон рас­пределения.

Смысл параметров нормального распределения наглядно показан на рис. 14.

Величина j(х) стремится к нулю при x ® –¥ и x ® +¥. График функции j(х) симметричен относительно точки а. При этом в точке а функция j(х) достигает своего максимума, который равен .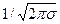

Параметр а характеризует положение графика функции на числовой оси (параметр положения). Параметр s (s > 0) ха­рактеризует степень сжатия или растяжения графика плотно­сти (параметр масштаба). Как видим, вся совокупность нор­мальных распределений представляет собой двухпараметри­ческое семейство.

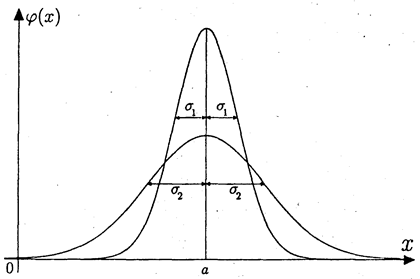
Рис. 14. Кривая нормального распределения со средним а и различными значениями дисперсии s²

Нормальный закон характеризуется формулой вида:

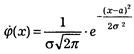
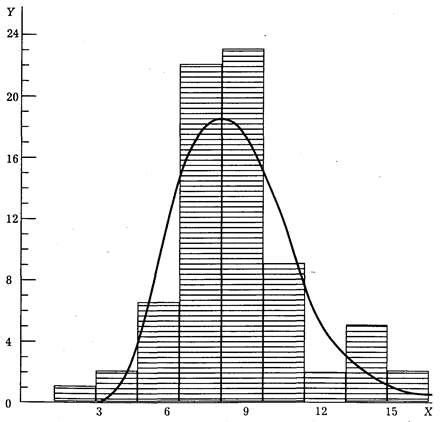
Рис. 15. Иллюстрация нормального закона из сферы криминологии

(данные автора и кандидата физико-математических наук Крупина В. Г.)

На горизонтальной оси (0Х) отложено число убийств на 100 000 жителей. На вертикальной оси (0Y) отложены числа регионов, соответствующие конкретному числу убийств на 100 000 жителей. Ступенчатая линия — гистограмма статистического распределения. Кривая линия очень близка к нормальному распределению (однако несколько скошена вправо).

В криминологических исследованиях нередко встречают­ся асимметричные распределения (рис. 16).

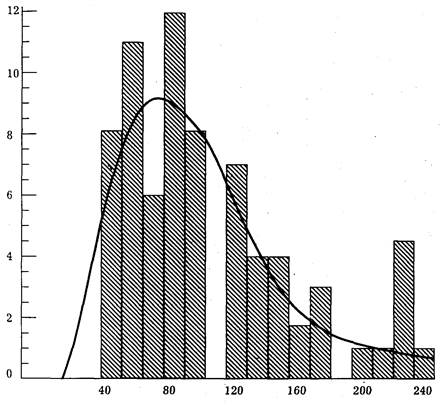
Рис. 16. Статистическое распределение числа краж на 100 000 жителей регионов РФ

(данные автора и кандидата физико-математических наук Крупина В. Г.)

Главная особенность нормального закона состоит в том, что он является предельным, к которому приближаются дру­гие законы распределения при весьма часто встречающихся типичных ситуациях.

На горизонтальной оси отложено число краж на 100 000 жителей. На вертикальной — число регионов, соответствующее числу краж. Два раз­рыва означают, что регионы РФ в криминологическом плане представ­ляют собой как бы самостоятельные образования.

Тесно связан с нормальным распределением закон Пуас­сона.

На практике случайные величины, распределенные по закону Пуассона, встречаются в случаях "редких событий", когда вероятность наступления отдельного события крайне мала.

Закон Пуассона применяется для описания числа несчаст­ных случаев, аварий в промышленности, редко встречающих­ся преступлений и т. д.

В распределении Пуассона исследуемая случайная вели­чина принимает значения 0, 1, 2,... Значения принимаются с вероятностью:

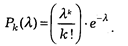
В этом выражении для распределения Пуассона параметр l — математическое ожидание и дисперсия.

Как видно, особенностью распределения Пуассона явля­ется то, что его математическое ожидание (l) равно диспер­сии.

В криминологии закон Пуассона используется для анали­за распределения автотранспортных происшествий, убийств и других правонарушений.

В конце XIX в. русский статистик А. Борткевич применил этот закон для изучения распределения смертей кавалеристов от ударов копыта лошади в 20 прусских корпусах за 10 лет. Теоретическая схема дала прекрасное совпадение с эмпири­ческими данными.

Дата добавления: 2015-04-25