Понятие функции

Нечеткие множества

Американский математик иранского происхождения Лотфи Заде разработал теорию нечетких множеств. Он исходил из того, что человеческому мышлению присуща такая черта, как оперирование размытыми понятиями и образами.

Примерами нечетких множеств являются: "высокий", "хо­роший", "грамотный", "срочность", "систематичность" и др. В области права наличие нечетких множеств подмечено уже давно. Они получили наименование оценочных понятий. Ти­пичными примерами оценочных понятий являются термины "существенный вред", "исключительный цинизм", "ведущая профессия", "крупный размер", "тяжкие последствия" и др.

С точки зрения требований законодательной техники не­обходимо превращать нечеткие понятия в четкие.*

* Преступление — это пример нечеткого множества. Состав преступле­ния — это уже четкое множество (понятие), характеризующееся стро­гими формальными рамками.

Л. Заде ввел в математику понятие лингвистической пе­ременной. Он определял ее как переменную, значения которой суть слова и предложения некоторого естественного или искусственного языка. Например, значениями понятия "скорость" могут быть: "медленная", "умеренная", "большая" и т. д.

Л. Заде нашел способ математически корректного описа­ния свойств нечетких множеств. Сама "нечеткость" обусловле­на заданием множества с помощью "лингвистической перемен­ной", т. е. слов или предложений естественного (или искусст­венного) языка.

Первый шаг заключается в нахождении "всех значений нечеткой переменной.

Степень принадлежности Х Î А элемента нечетному мно­жеству А характеризуется функцией принадлежности:

R_A (X).

Данная функция принимает значения между 0 и 1.

Возможно введение так называемых лингвистических ве­роятностей, которые имеют следующие значения: "правдопо­добно", "очень правдоподобно", "неправдоподобно", "чрезвы­чайно правдоподобно", "весьма правдоподобно" "вероятно", "невероятно", "более или менее вероятно", "маловероятно" и т. д. Для них в качестве базовой используется числовая пере­менная, принимающая значения на отрезке [0,1], а правила оперирования с такими вероятностями определяются с помо­щью операций над нечеткими множествами.

Наряду с понятием множества в математике важную роль играет понятие функции.

Переменная величина у называется функцией другой пе­ременной величины х, если каждому значению х из некото­рой области поставлено в соответствие вполне определенное значение величины у.

Для задания функции необходимо задать два множества (значений х и значений у) и закон соответствия между ними. Возможны различные способы задания этого соответствия: таб­личный, аналитический, графический и словесный.

Областью определения функции называется совокупность всех значений х, для которых определяются значения функ­ции у.

Областью изменения функции у = f(x) называется сово­купность всех значений, принимаемых у, когда х принимает все возможные значения из области определения функции.

К основным элементарным функциям относятся следующие:

1) степенная функция: у = xⁿ, где п — вещественное чис­ло;

2) показательная, функция: у = a^х, где а > 0 и а ¹ 1;

3) логарифмическая функция: у = log _ax, где а > 0 и а ¹ 1;

4) тригонометрические функции: у = sin х, у = cos х, у = tg x и т. д.;

5) обратные тригонометрические функции: у = arcsin х, у = arccos x: и т. д.

Обобщением понятия числовой функции является поня­тие предметной функции — когда М₁ и М₀ — вообще какие-то предметы (или числа). Так, словосочетание "год рождения" может трактоваться как функция, которая переводит класс людей в класс своеобразных чисел — временных дат.

Аналогичной является функция "возраст" и вообще такие выражения языка, как "скорость", "объем", "плотность" и т. п.

Выражение "место рождения" (человека) как функция соотносит каждому человеку город, село, деревню и т. п.

Другой вид функций, введенных логикой, — это логичес­кие функции. Они отличаются от предметных функций своеоб­разием своих значений.

Таковыми являются и — "истина" или л — "ложь".

В сфере права и правовой информатики применяются раз­личные функции. Их познавательная роль различна. В сфере со­циального прогнозирования функциональная зависимость исполь­зуется для описания рядов динамики какого-либо процесса.

Так, в сфере права немалую роль играет логистическая кривая. Она описывает процессы с насыщением. Логистическая функция описывается уравнением вида:

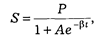
где Р — предельное значение переменной, барьер или потолок,

b — константа, характеризующая наклон кривой,

е — постоянная величина,

t — реальное время,

S — исследуемая переменная.

Логистическая функция в стандартной форме отображает многие социальные процессы, кривая развития которых рас­падается на две ветви: экспоненциально возрастающую и ло­гарифмически затухающую. Так, динамика перспективного роста народонаселения земного шара близко следует S -образ­ной логистической кривой.

В условиях административно-командной системы показа­тели зарегистрированной преступности в России были весьма умеренными. Начиная с 1989 г. они резко пошли вверх.*

* Прирост по годам: 1989 — 32,7%; 1990 — 13,6%; 1991 — 17,9%; 1992 — 27,3%.

В 1993 г. в динамике преступности наступил резкий пере­лом. Зарегистрированная преступность продолжала расти, но уже гораздо более медленными темпами.* Следовательно, про­изошло определенное насыщение общества преступными про­явлениями. Определенный уровень криминогенного потенциа­ла общества оказался исчерпанным.

* Прирост составлял: в 1993 г.— 1,4%; 1994 — (-6,0%), т. е. падение на 6%!; 1995 — 4,7%, 1996 — (-4,7%), 1997 — (-8,7% — падение), 1998 — 7,7%, 1999 — 18% (снова значительный рост).

Логистическая кривая удобна для описания процессов ди­намики числа нормативных актов. На первом этапе формиро­вания нового законодательства процесс идет довольно мед­ленно. Затем он ускоряется нарастающими темпами. После определенного порога темпы роста начинают снижаться и медленно приближаются к некоторой постоянной величине (асимптоте).

Дата добавления: 2015-04-25