Уравнение движения электропривода 2 страница

В соответствии с законом Ньютона поступательное движение описывается, как , (3.1)

где F - движущая сила, F_c - сила сопротивления, - инерционная сила.

Для вращательного движения это уравнение имеет аналогичный вид

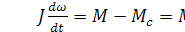(3.2)

Здесь аналогом массы является суммарный приведенный к валу двигателя момент инерции J, вместо линейной скорости V рассматривается угловая скорость двигателя w, а в правую часть уравнения входят момент двигателя М и статический момент сопротивления механизма М_с. Динамический момент , равный разности движущего и момента сопротивления, пропорционален угловому ускорению электропривода.

Уравнение (3.2) в электроприводе получило название «уравнение движения», по которому динамический момент возникает только в переходных режимах, т. е. тогда, когда меняется кинетическая энергия при ускорении и замедлении электропривода. Приведенные уравнения (3.1) и (3.2) можно применять лишь для электроприводов с J=const.

В общем случае выражение для определения динамического момента 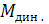можно определить из уравнения запаса кинетической энергии для вращающегося тела:

(3.3)

где J = m · r ² – момент инерции тела, обладающего массой m;

r – радиус вращающегося тела правильной цилиндрической формы.

Мощность, которую вращающиеся массы получают при ускорении электропривода или отдают при торможении:

(3.4)

Тогда, динамический момент можно найти с учетом :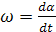

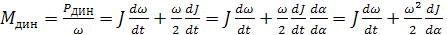. (3.5)

Уравнение для определения динамического момента состоит из двух составляющих: первое из них определяет изменение динамического момента при изменении угловой скорости ω электропривода, второе - при изменении его момента инерции во времени или угла поворота α вращающегося рабочего механизма.

У поступательно движущегося рабочего механизма со скоростью V и массой m динамическая составляющая мощности определяется из запаса кинетической энергии:

(3.6)

Динамическое усилие на рабочем органе определяется:

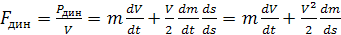, (3.7)

где динамическое усилие определяется ускорением поступательно движущегося рабочего органа и изменением массы при движении рабочего органа.

В качестве примеров изменения момента инерции в уравнении (3.5) можно привести зависимость момента инерции барабана с многослойной навивкой каната подъемной установки от глубины подъема, изменение момента инерции кабельного барабана в установках кабельного производства. Примером изменения массы при поступательном движении рабочего механизма является изменение массы ковша при черпании грунта экскаватором - драглайном, изменение массы груза ленточного конвейера.

Рассмотренные выше условия изменения в уравнениях движения электропривода возникают при работе машин, в которых перемещение рабочего органа по пространственным траекториям осуществляется несколькими индивидуальными электроприводами, предусмотренными для каждой координаты перемещения (экскаваторы, краны, роботы и т.п.).

В подобных случаях приведенный момент инерции электропривода, как и статический момент сопротивления, следует полагать независимой функцией времени J(t). Тогда уравнение движения электропривода примет вид:

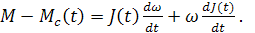(3.8)

Функции J(t) и M_c(t) при этом следует определить путем анализа движения электропривода, вызывающего изменения момента инерции и нагрузки.

Полученные математические описания динамических процессов в механической части электропривода, представляемой уравнениями движения, позволяют анализировать возможные режимы движения электропривода. Условием динамического процесса в системе, описываемой (3.8), является dw/dt¹0, т.е. наличие изменений скорости электропривода.

Для анализа статических режимов работы электропривода необходимо положить dw/dt=0.

Дата добавления: 2015-04-25