Определение. Частные производные вида и т.д. называются смешанными производными. 2 страница

С геометрической точки зрения D - площадь фигуры, ограниченной контуром.

Разобьем область D на n частичных областей сеткой прямых, отстоящих друг от друга по оси х на расстояние Dх_i, а по оси у – на Dу_i. Вообще говоря, такой порядок разбиения наобязателен, возможно разбиение области на частичные участки произвольной формы и размера.

Получаем, что площадь S делится на элементарные прямоугольники, площади которых равны S_i = Dx_i × Dy_i.

В каждой частичной области возьмем произвольную точку Р(х_i, y_i) и составим интегральную сумму

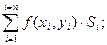
где f – функция непрерывная и однозначная для всех точек области D.

Если бесконечно увеличивать количество частичных областей D_i, тогда, очевидно, площадь каждого частичного участка S_i стремится к нулю.

Определение: Если при стремлении к нулю шага разбиения области D интегральные суммы 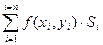имеют конечный предел, то этот предел называется двойным интегралом от функции f(x, y) по области D.

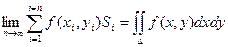
С учетом того, что S_i = Dx_i × Dy_i получаем:

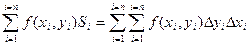
В приведенной выше записи имеются два знака S, т.к. суммирование производится по двум переменным х и у.

Т.к. деление области интегрирования произвольно, также произволен и выбор точек Р_i, то, считая все площади S_i одинаковыми, получаем формулу:

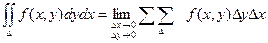
Условия существования двойного интеграла.

Сформулируем достаточные условия существования двойного интеграла.

Теорема. Если функция f(x, y) непрерывна в замкнутой области D, то двойной интеграл 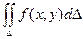существует.

Теорема. Если функция f(x, y) ограничена в замкнутой области D и непрерывна в ней всюду, кроме конечного числа кусочно – гладких линий, то двойной интеграл 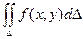существует.

Свойства двойного интеграла.

1)

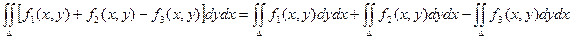
2)

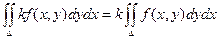
3) Если D = D₁ + D₂, то

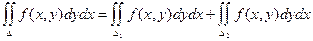
4) Теорема о среднем. Двойной интеграл от функции f(x, y) равен произведению значения этой функции в некоторой точке области интегрирования на площадь области интегрирования.

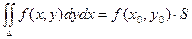
5) Если f(x, y) ³ 0 в области D, то .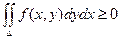

6) Если f₁(x, y) £ f₂(x, y), то .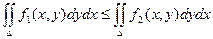

7) .

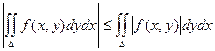Вычисление двойного интеграла.

Теорема. Если функция f(x, y) непрерывна в замкнутой области D, ограниченной линиями х = a, x = b, (a < b), y = j(x), y = y(x), где j и y - непрерывные функции и

j £ y, тогда

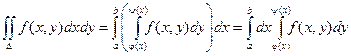
y y = y(x)

D

y = j(x)

a b x

Пример. Вычислить интеграл 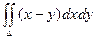, если область D ограничена линиями: y = 0, y = x², x = 2.

y

D

0 2 x

=

=

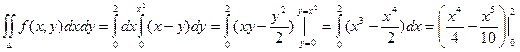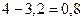
Теорема. Если функция f(x, y) непрерывна в замкнутой области D, ограниченной линиями y = c, y = d (c < d), x = F(y), x = Y(y) (F(y) £ Y(y)), то

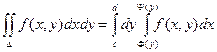
Пример. Вычислить интеграл 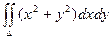, если область D ограничена линиями y = x, x = 0, y = 1, y = 2.

y

y = x

D

0 x

Пример. Вычислить интеграл 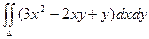, если область интегрирования D ограничена линиями х = 0, х = у², у = 2.

=

=

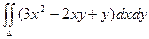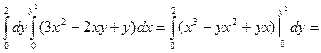
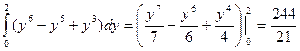
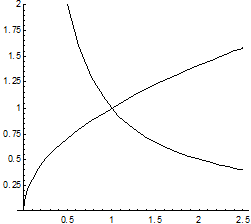
Пример. Вычислить двойной интеграл 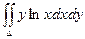, если область интегрирования ограничена линиями ху=1, у = 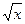, х = 2.

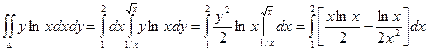
1.

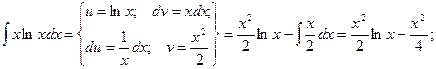
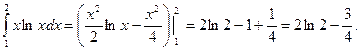
2.

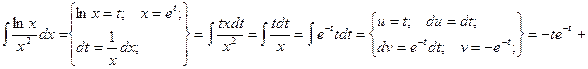
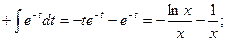
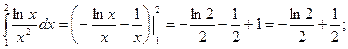
3.

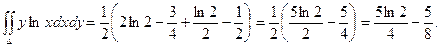
Замена переменных в двойном интеграле.

Расмотрим двойной интеграл вида 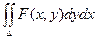, где переменная х изменяется в пределах от a до b, а переменная у – от j₁(x) до j₂(х).

Положим х = f(u, v); y = j(u, v)

Тогда dx = 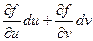; dy = ;

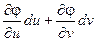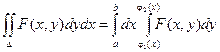
т.к. при первом интегрировании переменная х принимается за постоянную, то dx = 0.

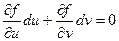, т.е.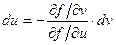

пожставляя это выражение в записанное выше соотношение для dy, получаем:

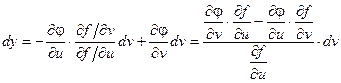
Выражение 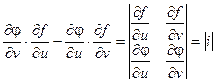называется определителем Якоби или Якобианом функций f(u, v) и j(u, v).

(Якоби Карл Густав Якоб – (1804-1851) – немецкий математик)

Тогда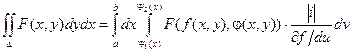

Т.к. при первом интегрировании приведенное выше выражение для dx принимает вид 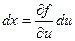(при первом интегрировании полагаем v = const, dv = 0), то при изменении порядка интегрирования, получаем соотношение:

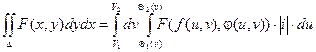
Двойной интеграл в полярных координатах.

Воспользуемся формулой замены переменных:

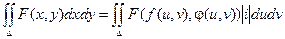
При этом известно, что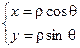

В этом случае Якобиан имеет вид:

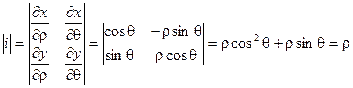
Тогда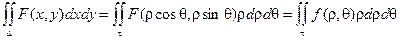

Здесь t - новая область значений,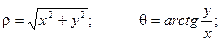

Тройной интеграл.

При рассмотрении тройного инеграла не будем подробно останавливаться на всех тех теоретических выкладках, которые были детально разобраны применительно к двойному интегралу, т.к. существенных различий между ними нет.

Единственное отличие заключается в том, что при нахождении тройного интеграла интегрирование ведется не по двум, а по трем переменным, а областью интегрирования является не часть плоскости, а некоторая область в техмерном пространстве.

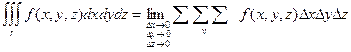
Суммирование производится по области v, которая ограничена некоторой поверхностью j(x, y, z) = 0.

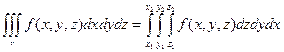
Здесь х₁ и х₂ – постоянные величины, у₁ и у₂ – могут быть некоторыми функциями от х или постоянными величинами, z₁ и z₂ – могут быть функциями от х и у или постоянными величинами.

Пример. Вычислить интеграл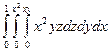

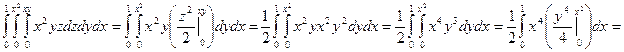
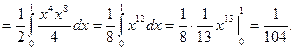
Замена переменных в тройном интеграле.

Операция замены переменных в тройном интеграле аналогична соответсвующей операции для двойного интеграла.

Можно записать:

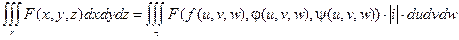
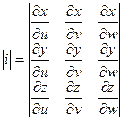
Наиболее часто к замене переменной в тройном интеграле прибегают с целью перейти от декартовой прямоугольной системы координат к цилиндрической или сферической системе.

Рассмотрим эти преобразования подробнее.

Цилиндрическая система координат.

z

P

z

q x

r

y

Связь координат произвольной точки Р пространства в цилиндрической системе с координатами в декартовой прямоугольной системе осуществляется по формулам:

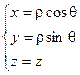
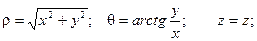
Для представления тройного интеграла в цилиндрических координатах вычисляем Якобиан:

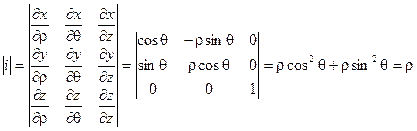
Итого: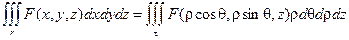

Сферическая система координат.

z

P

r

j

0 q x

y

Связь координат произвольной точки Р пространства в сферической системе с координатами в декартовой прямоугольной системе осуществляется по формулам:

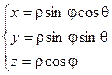
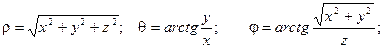
Для представления тройного интеграла в сферических координатах вычисляем Якобиан:

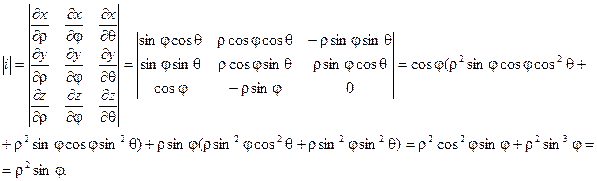
Окончательно получаем:

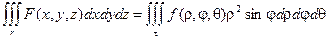
Геометрические и физические приложения кратных интегралов.

1) Вычисление площадей в декартовых координатах.

y

y = j(x)

S

y = f(x)

a b x

Площадь S, показанная на рисунке может быть вычислена с помощью двойного интеграла по формуле:

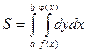
Пример. Вычислить площадь фигуры, ограниченной линиями y² = 4x + 4;

x + y – 2 = 0.

Построим графики заданных функций:

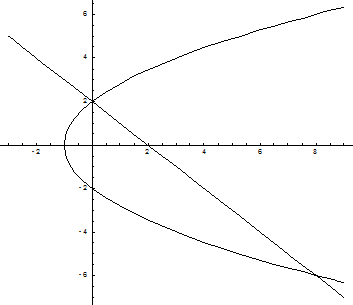
Линии пересекаются в двух точках – (0, 2) и (8, -6). Таким образом, область интегрирования ограничена по оси Ох графиками кривых от 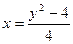до х = 2 – у, а по оси Оу – от –6 до 2. Тогда искомая площадь равна:

S =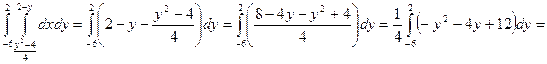

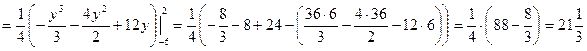
2) Вычисление площадей в полярных координатах.

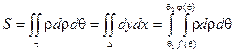
3) Вычисление объемов тел.

Пусть тело ограничено снизу плосткостью ху, а сверху– поверхностью z = f(x,y),

а с боков – цилиндрической поверхностью.

Такое тело называется цилиндроид.

z

z = f(x, y)

x₁ y₁ x₂

x

y₂

y

V =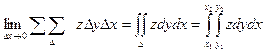

Пример. Вычислить объем, ограниченный поверхностями: x² + y² = 1;

x + y + z =3 и плоскостью ХОY.

Пределы интегрирования: по оси ОХ: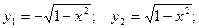

по оси ОY: x₁ = -1; x₂ = 1;

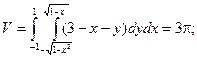
4) Вычисление площади кривой поверхности.

Если поверхность задана уравнением: f(x, y, z) = 0, то площадь ее поверхности находится по формуле:

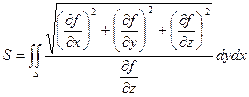
Если поверхность задана в неявном виде, т.е. уравнением z = j(x, y), то площадь этой поверхности вычисляется по формуле:

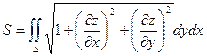
5)Вычисление моментов инерции площадей плоских фигур.

Пусть площадь плоской фигуры (область D) ограничена линией, уравнение которой f(x,y) = 0. Тогда моменты инерции этой фигуры находятся по формулам:

- относительно оси Ох: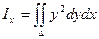

- относительно оси Оу: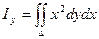

- относительно начала координат: 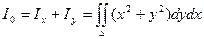- этот момент инерции называют еще полярным моментом инерции.

6) Вычисление центров тяжести площадей плоских фигур.

Координаты центра тяжести находятся по формулам:

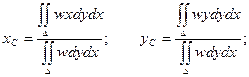
здесь w – поверхностная плотность (dm = wdydx – масса элемента площади).

7) Вычисление объемов тел с помощью тройного интеграла.

Если поверхность тела описывается уравнением f(x, y, z) = 0, то объем тела может быть найден по формуле:

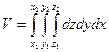
при этом z₁ и z₂ – функции от х и у или постоянные, у₁ и у₂ – функции от х или постоянные, х₁ и х₂ – постоянные.

8) Координаты центра тяжести тела.

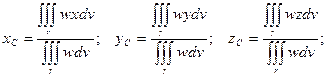
9) Моменты инерции тела относительно осей координат.

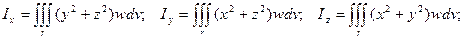
10) Моменты инерции тела относительно координатных плоскостей.

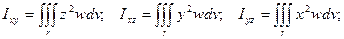
11) Момент инерции тела относительно начала координат.

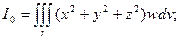
В приведенных выше формулах п.п. 8 – 11 r – область вычисления интеграла по объему, w – плотность тела в точке (х, у, z), dv – элемент объема

- в декартовых координатах: dv = dxdydz;

- в циллиндрических координатах: dv = rdzdjdq;

- в сферических координатах: dv = r²sinjdrdjdq.

12) Вычисление массы неоднородного тела.

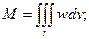
Теперь плотность w – величина переменная.

Дата добавления: 2015-04-25