Дифференциальное уравнение вида

Уравнения однородные и приводящиеся к ним.

А. 1.Функция f(x,y) называется однородной функцией k-ой степени, если справедливо тождество

F(tx,ty)=t^kf(x,y).

M(x,y)dx+N(x,y)dy=0

называется однородным, если коэффициенты М(х,у) и N(х,у) – однородные функции одной и той же степени. Однородные уравнения могут быть записаны в виде

,

где f(x,y) однородная функция нулевой степени.

Однородное уравнение при помощи подстановки у=ux, где u(x) – новая неизвестная функция, преобразуется в уравнение с разделяющимися переменными. Можно также принять подстановку x=uy.

2. Уравнение вида

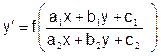
приводится к однородному с помощью замены переменных х и у по формулам х=х₀+, у=у₀+, где  – новые переменные, х₀,у₀ – решение системы уравнений

3.Некоторые уравнения можно привести к однородным заменой y=z^a Число  обычно заранее неизвестно. Чтобы его найти, надо в уравнении сделать замену y=z^a. Требуя, чтобы уравнение было однородным, найдем число , если это возможно. Если же этого сделать нельзя, то уравнение не приводится к однородному этим способом.

B. Задачи и упражнения для самостоятельного решения.

10.(x+y-2)dx+(x-y+4)dy=0.

11. (x+y)dx+(x-y-2)dy=0.

12. 2x+3y-5+(3x+2y-5)y'=0.

13. 2xy'(x-y²)+y³=0.

14. 4y⁶+x³=6xy⁵y'.

15.

16. (x+y³)dx+3(y³-x)y²dy=0.

18.Найти кривую, обладающую тем свойством, что величина перпендикуляра, опущенного из начала координат на касательную, равна абсциссе точки касания.

19.Определить кривую, у которой отношение отрезка, отсекаемого касательной на оси Оу, к радиусу-вектору равно постоянной величине.

20.Найти кривую, для которой длина отрезка, отсекаемого на оси ординат нормалью, проведенной к какой-нибудь точке кривой, равна расстоянию до этой точки от начала координат.

С. Примеры решения задач.

1₀.Решить уравнение xdy=(x+y)dx.

Решение. Это уравнение однородное. Полагаем y=ux. Тогда dy=udx+xdu. Подставляя в уравнение, получим

x(xdu+udx)=(x+ux)dx; xdu=dx.

Решаем полученное уравнение с разделяющимися переменными

Возвращаясь к старому переменному у, получим y=x(lnx+C). Кроме того, имеется решение х=0, которое было потеряно при деление на х.

2₀. Решить уравнение (x+y-2)dx+(x-y+4)dy=0.

Дата добавления: 2015-04-25