Дифференциальные уравнения первого порядка

Основные понятия и определения.

А. Уравнение, связывающее независимую переменную х, неизвестную функцию у=у(х) и её первую производную у^/, называется обыкновенным дифференциальным уравнением первого порядка.

Оно имеет вид

F(x,y,y^/)=0, (1)

или вид

y^/=f(x,y), (2)

где F(x,y,y^/) и f(x,y) заданные функции своих аргументов. Часто встречается и такая запись дифференциального уравнения:

P(x,y)dx+Q(x,y)dy=0. (3)

Решением дифференциального уравнения называется функция y=j(x), которая будучи поставленной в уравнение, обращает его в тождество относительно переменной x.

Если решение дифференциального уравнения задано в неявном виде Ф(x,y)=0, то оно обычно называется интегралом.

График решения дифференциального уравнения называется интегральной кривой.

Процесс нахождения решения дифференциального уравнения называется интегрированием.

Задачей Коши называют задачу нахождения решения y=y(x) уравнения (2), удовлетворяющего начальному условию

y(x_o)=y_o (4)

Теорема (существование и единственность решения задачи Коши). Если функция f(x,y) определена в замкнутой области и удовлетворяет в ней двум условиям:

1) непрерывна и, следовательно, ограничена, т.е. существует число , что ;

2) удовлетворяет относительно переменной y условию Липшица, т.е. для любых точек , что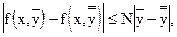

то уравнение (2) имеет единственное решение у=у(х), удовлетворяющее начальному условию (4), определенное и один раз непрерывно дифференцируемое в промежутке [x₀-h, x₀+h], где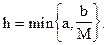

Общим решением дифференциального уравнения (1.2) называется функция зависящая от одной произвольной постоянной С и удовлетворяющая двум условиям:

1) она удовлетворяет уравнению (2) при любых допустимых значениях С;

2) каково бы ни было начальное условие (4), можно подобрать значение С₀ произвольной постоянной С, что решение будет удовлетворять заданному начальному условию (4).

Частным решением дифференциального уравнения (2) называется решение, которое получается из общего решения при фиксированном значении С.

Соотношение вида F(x,y,C)=0, неявно определяющее общее решение, называется общим интегралом дифференциального уравнения первого порядка.

B. Задачи и примеры для самостоятельного решения.

Выяснить, являются ли решениями (или интегралами), данных дифференциальных уравнений указанные функции:

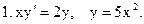
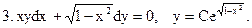
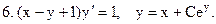
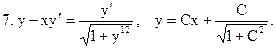
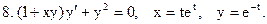
С. Примеры решения задач.

1₀. Показать, что функция является решением дифференциального уравнения .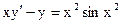

Решение. Вычислим производную данной функции

Отсюда

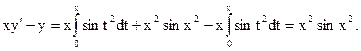
т.е. данная функция является решением дифференциального уравнения.

2₀. Доказать, что при каждом функция , определяемая соотношением , является решением дифференциального уравнения

Решение. Применяя к данному соотношению правило дифференцирования неявной функции, имеем

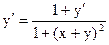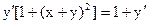Þ Þ Þ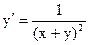

Подставляя найденное значение в данное дифференциальное уравнение, получаем тождество

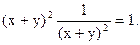
Уравнения с разделяющимися переменными.

А. Дифференциальное уравнение вида

называется уравнением с разделенными переменными.

Уравнение вида

,

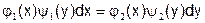в котором коэффициенты при дифференциалах распадаются на множители, зависящие только от x и только от у, называется уравнением с разделяющимися переменными.

Путем деления на произведение оно приводится к уравнению с разделенными переменными:

.

Общий интеграл этого уравнения имеет вид

.

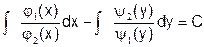Дифференциальное уравнение вида

,

где a, b и с – постоянные, заменой переменных 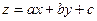преобразуются в уравнение с разделяющимися переменными.

.

В. Задачи и упражнения для самостоятельного решения.

Решить дифференциальные уравнения:

Решить дифференциальные уравнения, используя замену переменных.

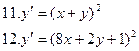
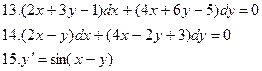
Найдите кривую, проходящую через точку (0,2), чтобы угловой коэффициент касательной в любой ее точке был равен ординате этой точки, увеличенной в три раза.

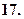Найти кривые, для которых площадь треугольника, образованного касательной, ординатой точки касания и осью абсцисс, есть величина постоянная, равная .

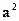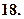Найти кривые, для которых сумма катетов треугольника, построенного как в предыдущей задаче, есть величина постоянная, равная .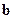

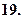Найти кривые, у которых точка пересечения любой касательной с осью абсцисс имеет абсциссу, вдвое меньше абсциссы точки касания.

Найти кривые, обладающие следующим свойством: отрезок оси абсцисс, отсекаемый касательной и нормалью, проведенными из произвольной точки кривой, равен .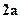

С. Примеры решения задач.

1₀. Решить уравнение .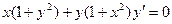

Решение. Представим данное уравнение в виде

.

Разделив обе части этого уравнения на , получим уравнение с разделенными переменными

.

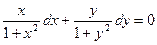Интегрируя это уравнение, находим

.

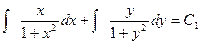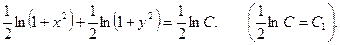
Отсюда .

2₀. Найти частное решение уравнения

,

удовлетворяющее начальному условию

Решение. Перепишем уравнение в виде

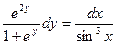
Отсюда

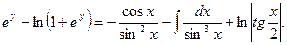
Таким образом,

Из условия находим 1-ln2=C, т.е. С=1-ln2.

Искомое решение определяется в неявном виде:

,

или

.

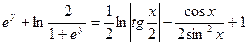3₀. Решить уравнение

.

Решение. Замена x-y-1=z приводит это уравнение к уравнению с разделяющимися переменными:

.

Функции z=2kp, k_Z являются решениями последнего уравнения. Остальные решения удовлетворяют соотношению

.

Отсюда

,

.

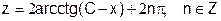Таким образом, .

Окончательно ,

.

4₀. Кривая y=j(x) проходит через точку (0,1) и обладает тем свойством, что в каждой ее точке тангенс угла наклона касательной к этой кривой равен удвоенному произведению координат точки касания. Найти кривую y=j(x).

Решение. Пусть (х,у) – произвольная точка на искомой кривой. Тангенс угла наклона касательной к кривой в точке (х,у) равен производной искомой функции в точке (х,у), т.е. у^. По условию у^=2ху. Отсюда . Так как у(0)=1, то С=1 и .

D. Ответы.

Дата добавления: 2015-04-25