Основные теоретические положения. Цель работы: 1. Изучить основные особенности режимов работы цепи однофазного синусоидального тока с последовательным соединением реостата

РЕАКТИВНЫХ ЭЛЕМЕНТОВ

ЦЕПЬ С ПОСЛЕДОВАТЕЛЬНЫМ СОЕДИНЕНИЕМ

Цель работы: 1. Изучить основные особенности режимов работы цепи однофазного синусоидального тока с последовательным соединением реостата, катушки индуктивности и конденсатора. 2. Получить навыки расчёта данной цепи и построения векторных диаграмм.

В разделе «Основные понятия о цепях синусоидального тока» дан анализ работы элементарных участков схемы с R-, L-, или с C- эле­ментом. Цепь с последовательным соединением реостата, катушки индуктивности и конденсатора на промышленной частоте (f 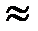50 Гц) можно представить, в общем случае, следующей схемой замещения (рис. 1). Промышленность выпускает конденсаторы с весьма малой проводимостью утечки. Т. е. в схеме (рис. 1) можно считать, что 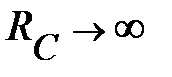, а 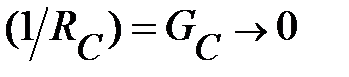. Тогда с учётом этого условия эквивалентная схема замещения примет вид (рис. 2). Полагаем все параметры схемы замещения (R, L, C, 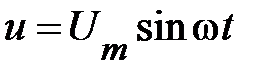) заданными.

Составим уравнение по II закону Кирхгофа (в мгновенной форме записи) для данной схемы (рис. 2):

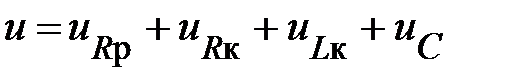. (1)

Учтём, что

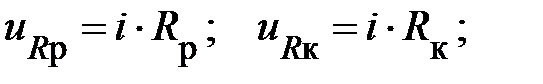
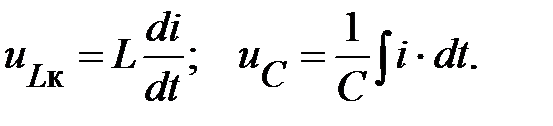
Тогда уравнение (1) примет вид

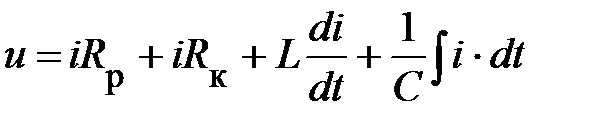(2)

По условию цепь подключена к источнику энергии с синусоидальным напряжением. Окончательно получим

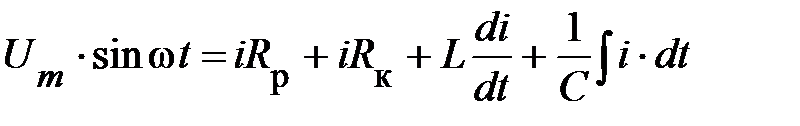. (3)

Данное уравнение является расчетным для классического метода расчета (не используя комплексные числа). Относительно неизвестного тока оно является линейным неоднородным интегро-диф­ферен­циальным уравнением. Его решение достаточно громоздко. Сложность решения классическим методом значительно возрастает, если имеем дело с системой таких уравнений, описывающих состояние многоконтурной линейной цепи синусоидального тока.

Рассмотрим решение этой задачи символическим методом. Запишем уравнение (3) в комплексной форме. В разделе «Основные понятия о цепях синусоидального тока» установили, что закон Ома на резистивном (R), индуктивном (L) и ёмкостном (С) элементах схемы можно записать в комплексной форме

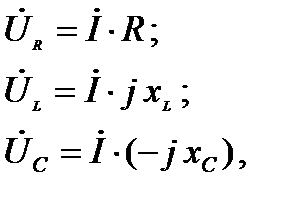(4)

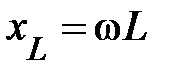где и 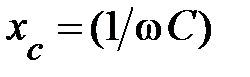, соответственно, индуктивное и ёмкостное сопротивление элементов.

С учётом соотношений (4) уравнение (2) в комплексной форме примет вид

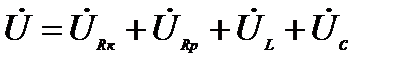(5)

или

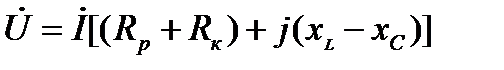. (6)

Уравнение (6) является расчетным уравнением при символическом методе расчета такой цепи. Относительно неизвестного комплекса тока оно является линейным алгебраическим уравнением, решение которого значительно проще, чем решение уравнения (3).

Таким образом, использование символического метода позволяет избежать операций интегрирования и дифференцирования при расчете цепей синусоидального тока и тем самым значительно упростить решение задачи.

Уравнение (6) устанавливает связь между напряжением 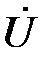, приложенным к схеме и током 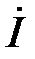, протекающим через эти элементы. Поэтому оно выражает закон Ома для данной схемы в символической (комплексной) форме.

Обозначим 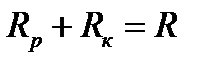. Сомножитель в квадратных скобках, входящий в уравнение (6), для линейной цепи не зависит от тока и напряжения

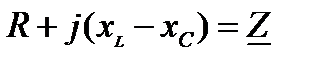(7)

и называется комплексным сопротивлением, данной схемы (учитывая, что 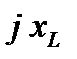и 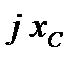также являются комплексными сопротивлениями отдельных элементов, 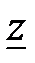иногда называют полным комплексным сопротивлением). Это сопротивление, как комплексное число, можно представить в показательной форме записи

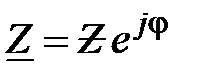, (8)

где 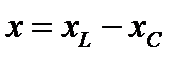– реактивная составляющая (или реактивное сопротивление), а 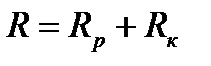– активная составляющая (или активное сопротивление) комплексного сопротивления данной схемы. Фазовый угол полного сопротивления

.

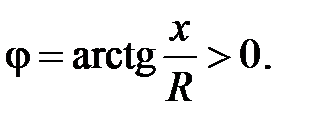Для наглядной иллюстрации возможных соотношений между активным и реактивными сопротивлениями схемы их изображают на комплексной плоскости в виде векторов. Построение соотношения (7) на комплексной плоскости начинают с выбора масштаба – (Ом/см). Откладывают от начала координат вдоль оси +1 отрезок ОК, в масштабе , равный (рис. 3). От конца этого отрезка параллельно полуоси 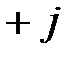откладывают отрезок КВ, в масштабе, равный 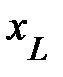. От его конца также параллельно оси мнимых чисел, но в противоположном направлении откладывают отрезок ВМ (или ВН), в масштабе, равный 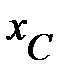. Подробное определение указанных отрезков и построение векторных диаграмм приведено в разделе «Основные понятия о цепях синусоидального тока».

Возможны в общем случае три варианта при построении треугольника сопротивлений (рис. 3):

1. 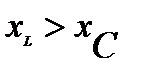. В этом случае треугольник сопротивлений ОКМ располагается выше оси +1. Для него 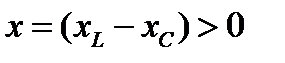и

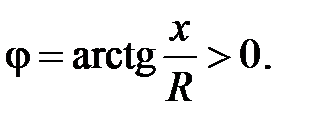
Для таких цепей, у которых превалирует индуктивное сопротивление, говорят, что сопротивление цепи (нагрузка) носит активно-индуктивный характер.

2. 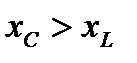. В этом случае треугольник сопротивлений ОКН располагается ниже оси 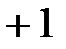. Для него 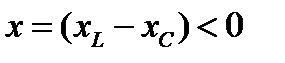и

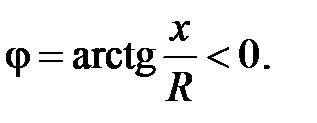
В этом случае сопротивление цепи (нагрузка) носит активно-ёмкостный характер.

3. 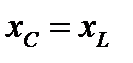. В соответствии с (7)

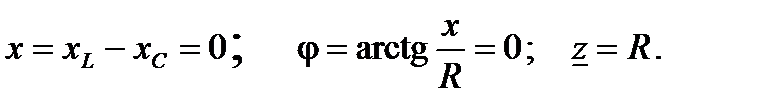
Треугольник сопротивлений вырождается в отрезок прямой ОК, и сопротивление цепи (нагрузка) носит чисто активный характер.

При заданном напряжении на выходе цепи 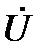соотношения между 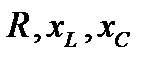полностью определяют режим работы цепи. Из соотношения (6) можно найти ток :

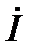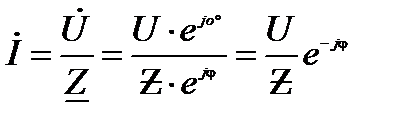(9)

Если 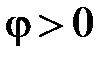(активно-индуктивный характер нагрузки), то из (9) следует, что ток 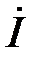отстаёт от напряжения 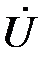по фазе на угол φ. Если 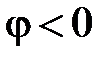(активно-ёмкостный характер нагрузки), то из (9) следует, что ток 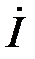опережает напряжение 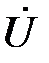на угол φ. Наконец, если 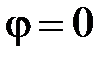(чисто активный характер нагрузки), то ток 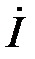совпадает с 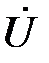по фазе.

Зная ток 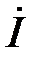можно определить падение напряжения на каждом элементе:

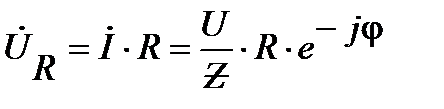– напряжение на эквивалентном резистивном элементе совпадает по фазе с током ;

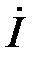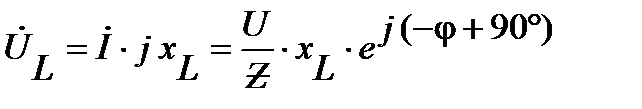– напряжение на индуктивном элементе опережает ток 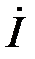на 90º по фазе;

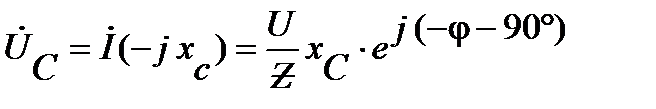– напряжение на ёмкостном элементе отстаёт от тока 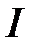на 90º по фазе;

На рис. 4, 5, 6 приведены векторные диаграммы, изображающие треугольники напряжений, которые соответствуют рассмотренным вариантам:

1. 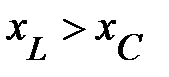– откуда вытекает, что 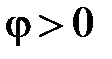, ток 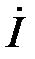отстает по фазе от общего напряжения 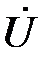на этот угол и действующие значения напряжений на реактивных элементах связаны соотношением 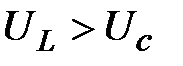(рис. 4);

2. 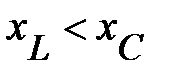откуда вытекает, что 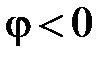, ток 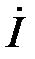опережает по фазе общее напряжение 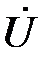на этот угол и действующие значения напряжений на реактивных элементах связаны соотношением 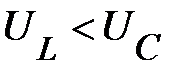(рис. 5);

3. 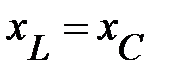откуда вытекает, что 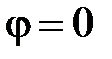, ток 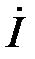совпадает по фазе с общим напряжением 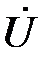и действующие значения напряжений на реактивных элементах связаны соотношением 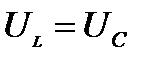(рис. 6).

Построение векторных диаграмм проводят аналогичным образом. Задаются масштабами по напряжению 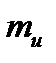(В/см) и току 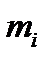(А/см). Определяют в соответствующем масштабе модули векторов. Построение начинают с вектора общего напряжения (оно задано в задаче). Его начальная фаза равна нулю, поэтому вдоль оси 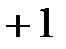от начала координат откладывают отрезок ОК пропорциональный величине 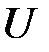и его конец отмечают стрелкой. Далее от оси 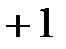откладывают угол 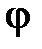в соответствии с его знаком и проводят луч ОВ. Вдоль луча откладывают отрезок ОВ пропорциональный величине 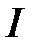, отмечая его конец стрелкой. Далее строится вектор 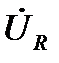, затем – 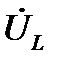, 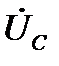и 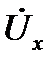в соответствии с их фазовыми углами относительно тока 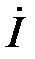(рис. 4 – 6). На указанных рисунках прямоугольные треугольники ОКН называют треугольниками напряжений.

Определить модули тока и напряжений на элементах такой схемы можно, не прибегая к комплексным числам и проводя расчёт в действующих значениях параметров режима. Для этого определяют модуль полного сопротивления цепи:

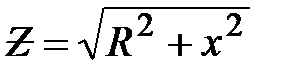, (10)

где 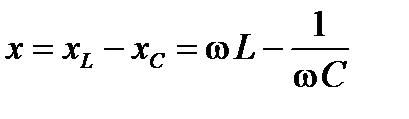. После чего определяют по заданному действующему значению напряжения 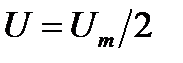действующее значение тока в цепи

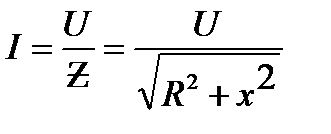(11)

и действующие значения напряжений на элементах

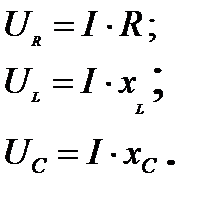(12)

Для построения векторной диаграммы необходимо определить сдвиг фазы между полным напряжением и током. Его определяют из треугольника сопротивлений (рис. 3)

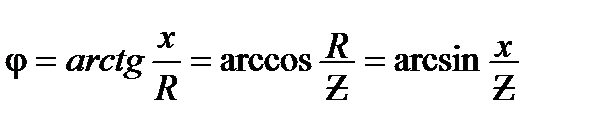(13)

или треугольника напряжений (рис. 4, 5)

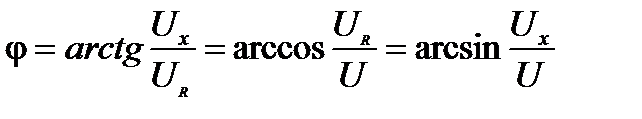(14)

где 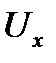– действующее значение реактивной составляющей падения напряжения

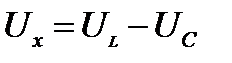(15)

Для поверки правильности вычислений можно определить 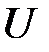, пользуясь найденными величинами

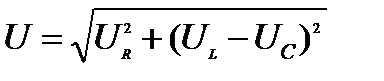(16)

Достоверность соотношения (16) вытекает из треугольника напряжений (рис. 4, 5, 6).

Рассмотрим энергетические процессы, протекающие в такой цепи. Мгновенная мощность на зажимах любой цепи, в том числе и данной, определится

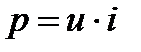(17)

Согласно уравнению (1), (2) соотношение (17) примет вид:

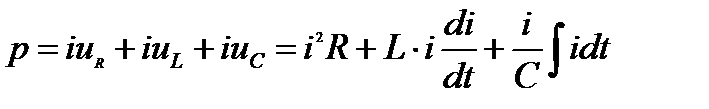(18)

Преобразуем слагаемые в соотношении (18)

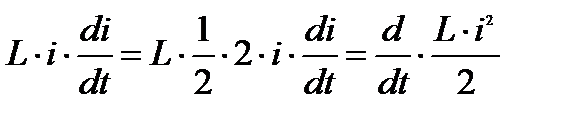(19)

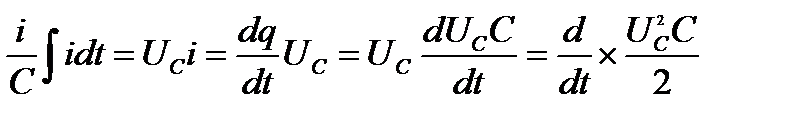(20)

Подставим (19) и (20) в (18) и получим

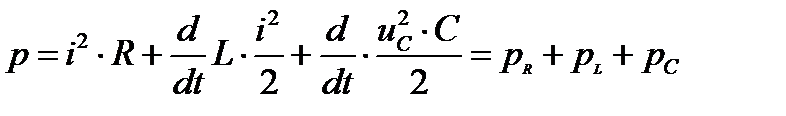, (21)

где 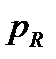– мгновенная мощность на участке цепи с резистивным элементом, определяющая безвозвратный расход энергии источника; 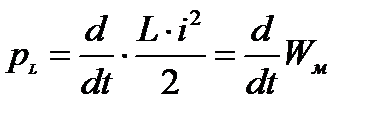– мощность на участке цепи с индуктивным элементом, определяющая скорость обмена энергией между магнитным полем 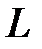-элемента и остальной цепью; 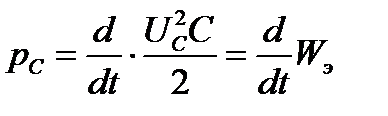– мощность на участке цепи с ёмкостным элементом, определяющая скорость обмена энергией между электрическим полем -элемента и остальной цепью.

Как видно из соотношения (21) всегда 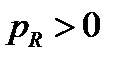. Т. е. резистивный элемент работает всегда в режиме приёмника и 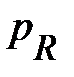характеризует необратимый процесс поглощения электроэнергии (с преобразованием в другие неэлектрические виды). Мощность 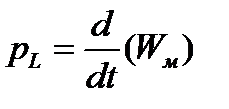определяет при 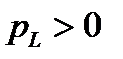скорость поступления энергии в магнитное поле 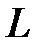-элемента при 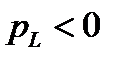– скорость возвращения энергии из этого поля. Аналогично 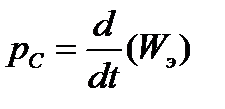определяет при 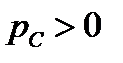скорость поступления энергии в электрическое поле -элемента, а при 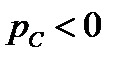– скорость возвращения энергии из этого поля. Определим суммарную мощность на 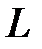и -элементах

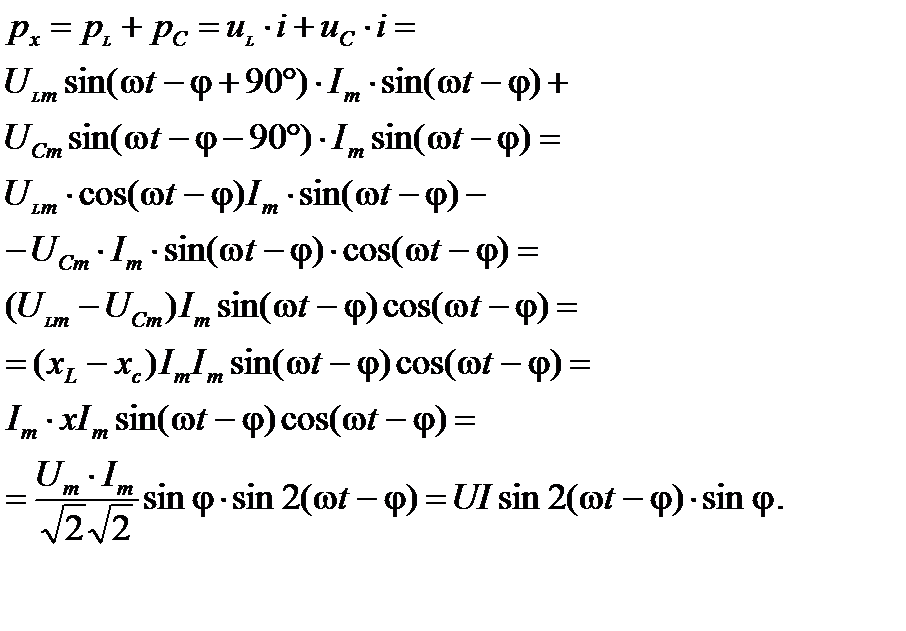(22)

Средняя мощность на 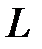и -элементах за время, кратное периоду, равна нулю, как интеграл от синусоидальной функции. Т. е. данные элементы безвозвратно энергию не потребляют. Амплитудное значение мгновенной мощности на этих элементах, определяемое как абсолютная величина реактивной мощности, определится

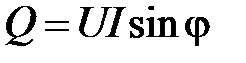(23)

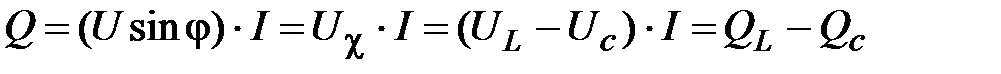(24)

Определим мгновенную мощность на резистивном элементе

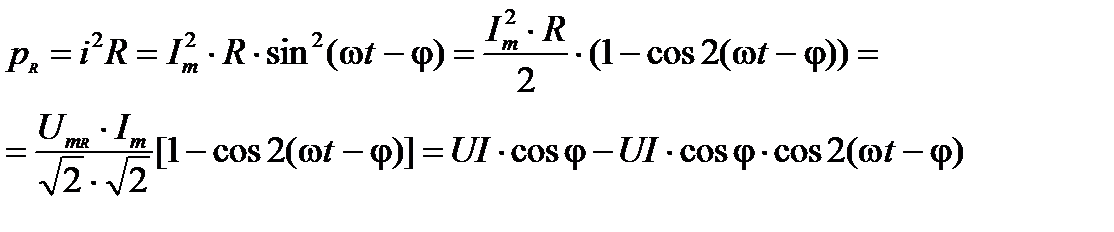(25)

Средняя мощность за время, кратное периоду на -элементе, определяемая, как активная мощность данной цепи, определится

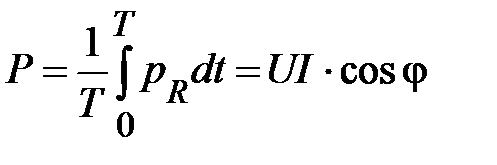(26)

В соответствии с формулами (23), (24), (25) полная мощность в данной цепи

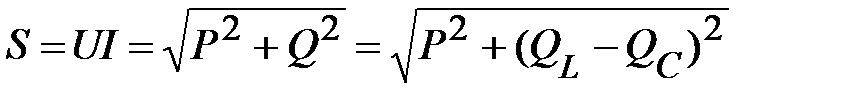. (27)

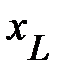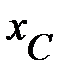Расположение треугольника мощностей, построенного по соотношению (27) зависит от значения параметров и схемы (рис. 2): при 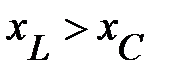он располагается выше оси (рис. 7); при 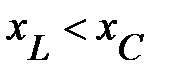– ниже оси 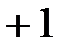(рис. 8); при 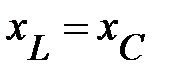– треугольник вырождается в отрезок прямой и мощность на зажимах цепи становится чисто активной (рис. 9).

Режим работы электрической цепи, содержащей катушку индуктивности и конденсатор, при котором напряжение на её зажимах и входной ток совпадают по фазе, называют резонансным.

Если указанные элементы соединены последовательно, то в такой цепи имеет место резонанс напряжений. Схема замещения этой цепи содержит последовательное соединение R-, L-, C -элементов (рис. 2). Условием резонанса напряжений будет равенство нулю реактивной составляющей входного комплексного сопротивления цепи

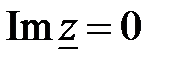(28)

Для данной цепи это условие, согласно (7),будет иметь место, если

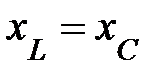(29)

или

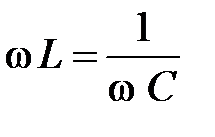(30)

Резонанса в данной цепи можно добиться, если:

а) изменять частоту питающего напряжения. Её величина при резонансе определяется из (30)

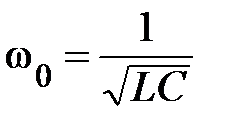; (31)

б) изменять индуктивность 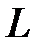– элемента

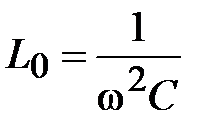; (32)

в) изменять ёмкость -элемента

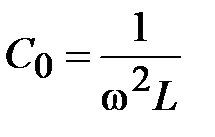. (33)

До резонанса 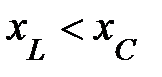и цепь носит активно-ёмкостный характер нагрузки. векторные диаграммы, соответствующие дорезонансным режимам работы цепи приведены на рис. 3, 5, 8.

При резонансе напряжений 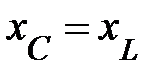и цепь носит чисто активный характер нагрузки. Векторные диаграммы резонансного режима приведены на рис. 3, 6, 9. как показано на рис. 6 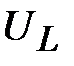и 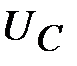полностью компенсируют друг друга, поскольку 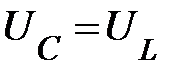и сдвиг фаз между синусоидами этих напряжений составляет 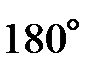(говорят, что эти напряжения колеблются в противофазе).

Для зарезонансной цепи 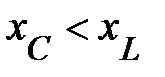и она носит активно-индуктивный характер нагрузки. Векторные диаграммы таких режимов приведены на рис. 3, 4, 7. Данная цепь, в которой возможен резонанс напряжений, называется последовательным резонансным контуром. Рассмотрим, как изменяются параметры режима работы цепи при изменении ёмкости. Допустим, цепь подключена к идеальному источнику ЭДС .

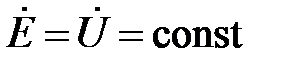Дата добавления: 2015-05-06