Полная проводимость цепи

.

.

.

.

.

.

.

Рассмотрим известное выражение для полной комплексной мощности

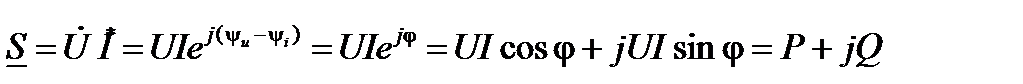. (27)

Таким образом, использование понятия о сопряженном комплексе тока позволяет реализовать аргумент полной комплексной мощности в виде разности фаз между синусоидами напряжения и тока (), а также установить корректную математическую связь между полной комплексной мощностью и ее составляющими (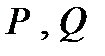). Проведем преобразование с сопряженными комплексами. В соответствии с (13) получим

В таком случае будем иметь

. ( 28)

Учтем, что

.

То есть для любого параметра произведение комплекса на сопряженный комплекс равно квадрату его модуля.

В соответствии с (27), (28) и (8) рассмотрим полную комплексную мощность

(29)

Треугольники мощностей, соответствующие выражению (29), приведены на рис. 9, 10, 11, которые иллюстрируют случаи:

– если , в этом случае , 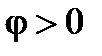(рис. 9). Т. е. реактивная мощность всей цепи является положительной величиной и во внешней цепи происходит обмен циркулирующей энергией исключительно между магнитным полем L -элемента и источником питания, а перезаряд С -элемента полностью осуществляется за счёт энергии магнитного поля L - элемента;

– если , в этом случае , (рис. 10). Т. е. реактивная мощность всей цепи является отрицательной величиной и во внешней цепи происходит обмен циркулирующей энергией исключительно между электрическим полем С -элемента и источником питания. Энергия в магнитное поле L -элемента полностью поступает при разряде С -элемента;

– наконец, если , в этом случае , а (рис. 11). Т. е. обмена энергией между источником питания и цепью не происходит. Вся энергия, поступающая от источника, безвозвратно потребляется цепью. При этом полная мощность на зажимах цепи чисто активная. Внутри цепи происходит циркулирующий обмен энергией одинаковой интенсивности между полями L, C -элементов.

Расчёт параметров режима работы цепи, построение векторной диаграммы, треугольников проводимостей и мощностей можно провести, не прибегая к комплексным числам. Расчёт проводят в действующих значениях параметров режима и в модулях параметров цепи. При этом возможны две методики расчёта:

· с использованием понятия об активной и реактивной составляющих тока в каждой ветви;

· с использованием понятия о полной проводимости цепи, ветви и составляющих этих проводимостей.

По первой методике, по известным параметрам цепи определяют полные сопротивления ветвей

Затем определяют полные токи в каждой ветви и составляющие этих токов

После чего определяют полный (входной) ток цепи

и его фазовый угол

Рассчитывают мощности на ветвях

мощности на всей схеме

Используя полученные результаты, определяют проводимости ветвей и всей схемы

Наконец, по полученным результатам с учётом знаков φ₁, φ₂ и φ строят векторные диаграммы токов, проводимостей и мощностей.

По второй методике, по известным параметрам цепи определяют проводимости ветвей и их фазовые углы

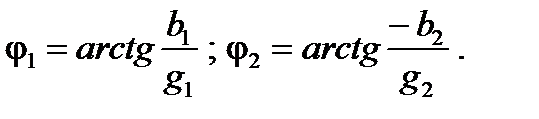
Затем определяют полную проводимость цепи и ее фазовый угол

После чего рассчитывают токи в ветвях и входной ток

Определяют мощности ветвей и всей цепи

И, наконец, зная величину и их знаки, строят векторные диаграммы токов, проводимостей и мощностей.

Иного характера расчёты проводят, если известны некоторые параметры режима работы цепи, и требуется определить параметры схемы замещения и построить векторную диаграмму. Такие расчёты проводят после экспериментального исследования схемы.

Например, дана схема замещения цепи (рис. 12). Путём эксперимента измерили следующие параметры режима работы этой цепи: P – активную мощность всей цепи; U – напряжение на зажимах цепи; I – входной ток; I ₁и I ₂ – токи ветвей; угол сдвига фаз между синусоидами напряжения 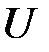и тока 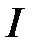(с учетом его знака). Необходимо определить параметры схемы и построить векторную диаграмму. Проводят следующие расчёты:

1. Определяют эквивалентные параметры всей цепи (знак общей реактивной проводимости 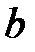и общего реактивного сопротивления 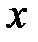определяется знаком измеренного угла )

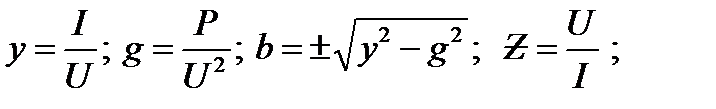
(30)

2. Определяют эквивалентные параметры каждой ветви

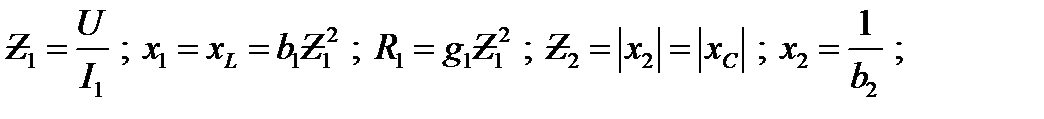(31)

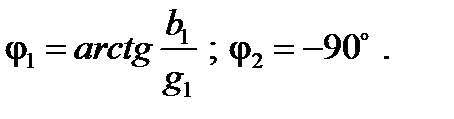
3. Определяют параметры элементов ветвей схемы

. (32)

4. Рассчитывают остальные параметры режима работы схемы

(33)

5. Строят векторные диаграммы токов, проводимостей, мощностей.

В данной цепи, как и в цепи с последовательным соединением R, L, C- элементов, возможен резонансный режим, который носит название резонанса токов. При резонансе токов в цепи, содержащей L и С- элементы, включённые в параллельные ветви, синусоиды входного тока I и напряжения 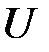, приложенного к зажимам цепи, совпадают по фазе, т. е. . Особенности этого режима уже рассмотрены (рис. 4, 8, 11). Определим резонансную частоту в цепи (рис. 1). Если для резонанса токов то в соответствии с (11)

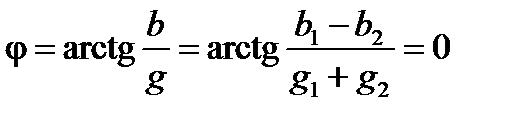
или

. (34)

Выражение (34) определяет условие резонанса токов для конкретной цепи. Если катушка индуктивности и конденсатор включены в параллельные ветви, то модули реактивных проводимостей ветвей должны быть равны.

.

Подставив эти выражения в (34) и решив уравнение относительно , получим

. (35)

Выражение (35) показывает, что резонансная частота определяется величиной четырёх параметров цепи L, C, R ₁, R ₂. Поэтому резонансного режима можно добиться, варьируя каждый из указанных параметров.

Проанализируем зависимости параметров контура и параметров режима его работы от изменения C на примере схемы рис. 12. Считаем, что величина ёмкости С изменяется от 0 до 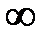, а цепь подключена к идеальному источнику синусоидальной ЭДС.

Дата добавления: 2015-05-06