
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Основные теоретические положения. Рассмотрим возможную схему замещения при параллельном соединении указанных приёмников (рис.1)
|
|
|
|
Рассмотрим возможную схему замещения при параллельном соединении указанных приёмников (рис.1). Используем символический метод расчета. Согласно 1 закону Кирхгофа для узла а можно записать
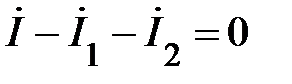 , (1)
, (1)
где 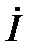 – ток в неразветвлённой части схемы или входной ток (на самом деле это комплекс действующего значения синусоидального входного тока. В целях краткого изложения материала такие величины будем называть ток, напряжение и тому подобное);
– ток в неразветвлённой части схемы или входной ток (на самом деле это комплекс действующего значения синусоидального входного тока. В целях краткого изложения материала такие величины будем называть ток, напряжение и тому подобное);  и
и 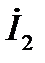 – соответственно, токи в ветвях схемы. Выразим слагаемые уравнения (1) через напряжение
– соответственно, токи в ветвях схемы. Выразим слагаемые уравнения (1) через напряжение  , воспользовавшись законом Ома
, воспользовавшись законом Ома
 (2)
(2)
где  – комплексное сопротивление первой ветви;
– комплексное сопротивление первой ветви; 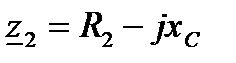 – комплексное сопротивление второй ветви. Тогда
– комплексное сопротивление второй ветви. Тогда
 . (3)
. (3)
В разделе «Основные понятия о цепях синусоидального тока» отмечено, что величина 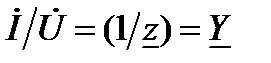 называется комплексной проводимостью. В данном случае эту величину можно обозначить как комплексную проводимость всей цепи. Из (3) получим
называется комплексной проводимостью. В данном случае эту величину можно обозначить как комплексную проводимость всей цепи. Из (3) получим
 , (4)
, (4)
где  – соответственно комплексная проводимость первой и второй ветви. Таким образом, при параллельном соединении ветвей эквивалентная комплексная проводимость всей схемы замещения равна сумме комплексных проводимостей ветвей.
– соответственно комплексная проводимость первой и второй ветви. Таким образом, при параллельном соединении ветвей эквивалентная комплексная проводимость всей схемы замещения равна сумме комплексных проводимостей ветвей.
Определим составляющие комплексных проводимостей каждой ветви. Отметим, что соотношения

справедливы только для всей ветви и не могут применяться в отношении отдельных её элементов. Рассмотрим составляющие комплексных проводимостей каждой ветви.
 , (5)
, (5)
где  – активная составляющая проводимости первой ветви;
– активная составляющая проводимости первой ветви; 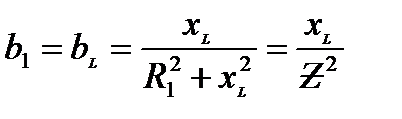 – реактивная составляющая проводимости первой ветви.
– реактивная составляющая проводимости первой ветви.
С учётом полученных соотношений
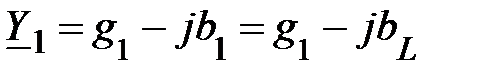 . (6)
. (6)
Рассуждая аналогично, для второй ветви, получим
 . (7)
. (7)
Тогда
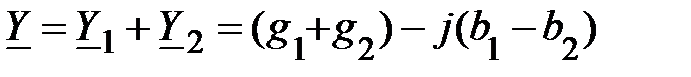 . (8)
. (8)
Положим, что синусоидальное напряжение на зажимах цепи определено выражением 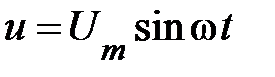 . В этом случае начальная фаза
. В этом случае начальная фаза  .
.
Комплексную проводимость всей схемы и отдельной ветви можно представить в показательной форме записи

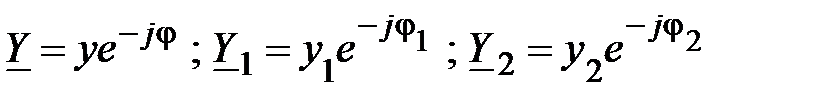 , (9)
, (9)
где  – соответственно, полная проводимость всей схемы, первой и второй ветви;
– соответственно, полная проводимость всей схемы, первой и второй ветви;  – фазовые углы указанных полных проводимостей. Они противоположны по знаку углам
– фазовые углы указанных полных проводимостей. Они противоположны по знаку углам  , определяющим сдвиг фаз между напряжением
, определяющим сдвиг фаз между напряжением  и, соответственно, током
и, соответственно, током  . При этом
. При этом
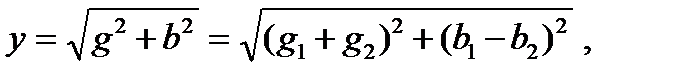
 ; (10)
; (10)
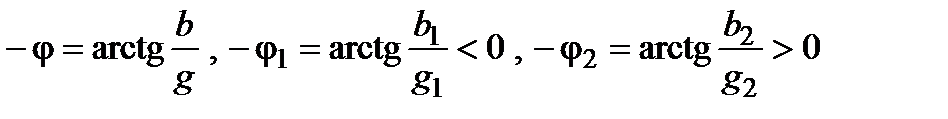 . (11)
. (11)
Рассмотрим влияние реактивных проводимостей на характер нагрузки цепи: 1. 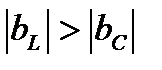 . Из (8) и (11) получим, что
. Из (8) и (11) получим, что  ,
, 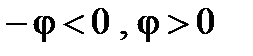 . При этом в данной схеме первая ветвь имеет активно-индуктивный характер нагрузки. Вторая ветвь – активно-ёмкостный характер нагрузки. На рис. 2 приведена векторная диаграмма проводимостей, соответствующая этому случаю. На векторной диаграмме действительные составляющие комплексных проводимостей (активные проводимости схемы
. При этом в данной схеме первая ветвь имеет активно-индуктивный характер нагрузки. Вторая ветвь – активно-ёмкостный характер нагрузки. На рис. 2 приведена векторная диаграмма проводимостей, соответствующая этому случаю. На векторной диаграмме действительные составляющие комплексных проводимостей (активные проводимости схемы  ) представлены векторами, совпадающими или параллельными оси
) представлены векторами, совпадающими или параллельными оси  . Мнимые составляющие комплексных проводимостей (реактивные проводимости схемы
. Мнимые составляющие комплексных проводимостей (реактивные проводимости схемы 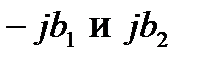 ) представлены векторами параллельными оси
) представлены векторами параллельными оси  в соответствии с их знаками. Кроме этого указаны как углы
в соответствии с их знаками. Кроме этого указаны как углы 
 , так и углы
, так и углы  . Учитывая условие 1, в целом, цепь имеет активно-индуктивный характер нагрузки. Прямоугольные треугольники OKN, NBC, OBM носят название треугольников проводимостей.
. Учитывая условие 1, в целом, цепь имеет активно-индуктивный характер нагрузки. Прямоугольные треугольники OKN, NBC, OBM носят название треугольников проводимостей.
Примечание. Направление угла сдвига фаз между напряжением и током принято отсчитывать от тока к напряжению. Поэтому с целью однообразного изложения анализа при построении векторных диаграмм (как и в работе №5) в дальнейшем на них указаны только углы 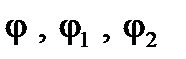 .
.
2. 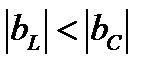 . Из (8) и (11) получим, что
. Из (8) и (11) получим, что  ,
,  . Характер нагрузки каждой ветви не меняется, но характер нагрузки всей схемы становится активно-ёмкостным. Векторная диаграмма, соответствующая этому случаю, приведена на рис. 3.
. Характер нагрузки каждой ветви не меняется, но характер нагрузки всей схемы становится активно-ёмкостным. Векторная диаграмма, соответствующая этому случаю, приведена на рис. 3.
3. 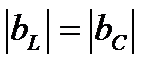 . Из (8) и (11) получим, что
. Из (8) и (11) получим, что  ,
,  . Характер нагрузки каждой ветви не меняется, но характер нагрузки всей схемы становится чисто активным. Векторная диаграмма, соответствующая этому случаю, приведена на рис. 4.
. Характер нагрузки каждой ветви не меняется, но характер нагрузки всей схемы становится чисто активным. Векторная диаграмма, соответствующая этому случаю, приведена на рис. 4.
Таким образом, в зависимости от соотношения 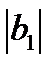 и
и  в схеме может происходить частичная или полная компенсация реактивных проводимостей ветвей. Это обстоятельство определяет характер нагрузки реальной цепи, величину и знак фазового угла
в схеме может происходить частичная или полная компенсация реактивных проводимостей ветвей. Это обстоятельство определяет характер нагрузки реальной цепи, величину и знак фазового угла  .
.
Из формул (8) и (10) следует, что
 (12)
(12)
Из (3) будем иметь
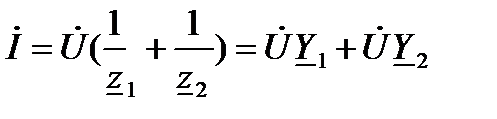 (13)
(13)
Учитывая (9), получим
 (14)
(14)
Слагаемые в правой части (14) имеют размерность А (Ампер). Их принято называть:  – комплекс активной составляющей действующего значения тока в первой ветви (в целях сокращения эту составляющую тока называют активной составляющей тока в первой ветви. Для остальных составляющих аналогично);
– комплекс активной составляющей действующего значения тока в первой ветви (в целях сокращения эту составляющую тока называют активной составляющей тока в первой ветви. Для остальных составляющих аналогично); 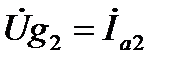 – комплекс активной составляющей тока во второй ветви;
– комплекс активной составляющей тока во второй ветви;  – комплекс реактивной составляющей тока в первой ветви;
– комплекс реактивной составляющей тока в первой ветви;  – комплекс реактивной составляющей тока во второй ветви. Тогда соотношение (14) можно переписать
– комплекс реактивной составляющей тока во второй ветви. Тогда соотношение (14) можно переписать
 . (15)
. (15)
Соотношению (15) соответствует уже другая эквивалентная схема замещения заданной цепи, состоящая из параллельного соединения активных и реактивных элементов проводимости (рис. 5).
Изобразим на комплексной плоскости соотношение (15). Поскольку  и
и 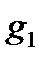 ,
,  – действительные числа, то вектора
– действительные числа, то вектора 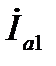 и
и 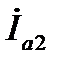 будут совпадать по направлению с вектором
будут совпадать по направлению с вектором 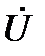 . Т. е. активные составляющие токов в ветвях совпадают по фазе с напряжением на зажимах схемы. вектора
. Т. е. активные составляющие токов в ветвях совпадают по фазе с напряжением на зажимах схемы. вектора 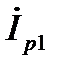 и
и  будут перпендикулярны вектору
будут перпендикулярны вектору 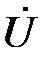 . При этом реактивная составляющая
. При этом реактивная составляющая  отстаёт на угол 90º по фазе, а реактивная составляющая
отстаёт на угол 90º по фазе, а реактивная составляющая  опережает на угол 90º по фазе указанное напряжение. Векторные диаграммы приведены на рис. 6, 7, 8. Они иллюстрируют возможные случаи:
опережает на угол 90º по фазе указанное напряжение. Векторные диаграммы приведены на рис. 6, 7, 8. Они иллюстрируют возможные случаи:
1. Если 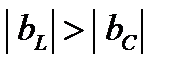 , в этом случае
, в этом случае 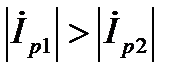 ,
, 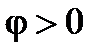 , то общий ток цепи
, то общий ток цепи  отстаёт по фазе от напряжения
отстаёт по фазе от напряжения 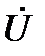 на угол
на угол  (рис. 6);
(рис. 6);
2. Если  , в этом случае
, в этом случае  ,
, 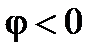 , то общий ток цепи
, то общий ток цепи  опережает по фазе напряжение
опережает по фазе напряжение  на угол φ (рис. 7);
на угол φ (рис. 7);
3. Наконец, если  , в этом случае
, в этом случае  ,
, 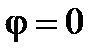 , то общий ток
, то общий ток  цепи совпадает по фазе с напряжением
цепи совпадает по фазе с напряжением  (рис. 8).
(рис. 8).
Следовательно, в цепи происходит частичная или полная компенсация реактивных составляющих токов в ветвях и в зависимости от этого полный (входной) ток  опережает, отстаёт или совпадает по фазе с напряжением
опережает, отстаёт или совпадает по фазе с напряжением  на зажимах цепи.
на зажимах цепи.
Рассмотрим энергетические процессы, протекающие в данной цепи (рис. 1).
Энергетический режим работы каждой ветви, как было установлено в разделе «Основные понятия о цепях синусоидального тока», определяется соотношением её активной и реактивной мощностей. Определим их величину
 . (16)
. (16)
Аналогично
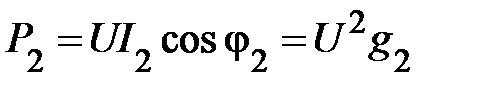 (17)
(17)
Т.е. активная или средняя за период мощность каждой ветви в разветвлённой цепи прямо пропорциональна активной проводимости этой ветви. Поскольку Р 1 и Р 2 в каждой ветви характеризуют интенсивность безвозвратного потребления энергии от источника питания, то общая активная мощность цепи равна арифметической сумме активных мощностей каждой ветви и пропорциональна активной проводимости всей цепи
 . (18)
. (18)
Определим реактивную мощность
 . (19)
. (19)
Аналогично
 . (20)
. (20)
Т. е. реактивная мощность каждой ветви в разветвлённой цепи прямо пропорциональна реактивной проводимости этой ветви. Для реактивных мощностей можно также записать
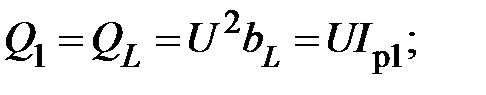 (21)
(21)
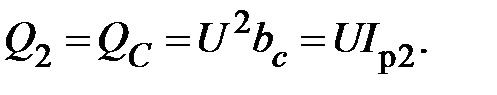 (22)
(22)
При одном и том же напряжении, приложенном к каждой ветви, реактивные составляющие токов этих ветвей 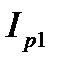 и
и  сдвинуты на 180º друг относительно друга. Следовательно, суммарная реактивная мощность равна разности реактивных мощностей в каждой ветви этой цепи
сдвинуты на 180º друг относительно друга. Следовательно, суммарная реактивная мощность равна разности реактивных мощностей в каждой ветви этой цепи
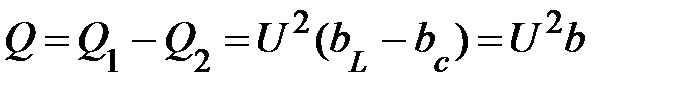 (23)
(23)
и пропорциональна реактивной проводимости всей цепи. Полная мощность каждой ветви равна
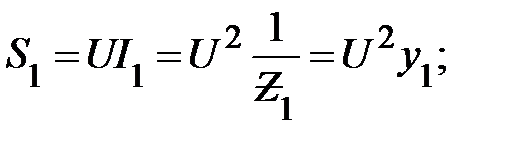 (24)
(24)
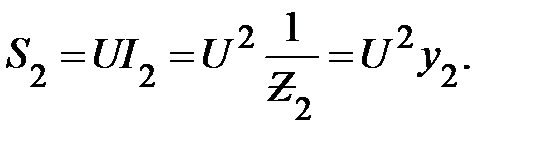 (25)
(25)
Т. е. полная мощность каждой ветви пропорциональна полной проводимости этой ветви. Определим полную мощность всей цепи
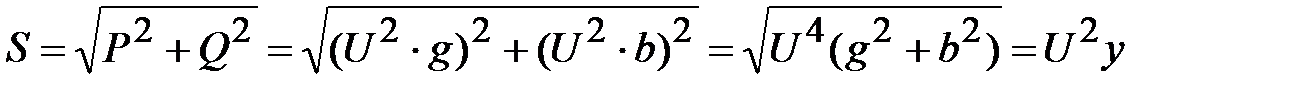 (26)
(26)
Т. е. полная мощность всей цепи пропорциональна проводимости этой цепи.
Для представления полной комплексной мощности с использованием проводимостей введем понятие о комплексно-сопряженных векторах.  – комплекс действующего значения напряжения,
– комплекс действующего значения напряжения, 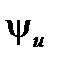 – начальная фаза соответствующей ему синусоиды,
– начальная фаза соответствующей ему синусоиды, 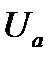 – активная и
– активная и 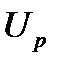 – реактивная составляющие этого комплекса (этого напряжения);
– реактивная составляющие этого комплекса (этого напряжения);  – сопряженный комплекс действующего значения напряжения и его аналогичные составляющие.
– сопряженный комплекс действующего значения напряжения и его аналогичные составляющие.
Такое же представление о сопряженном комплексе можно ввести для тока
 ;
;
для сопряженного комплексного сопротивления
 ;
;
для сопряженной комплексной проводимости
|
|
|
|
|
Дата добавления: 2015-05-06; Просмотров: 483; Нарушение авторских прав?; Мы поможем в написании вашей работы!