Метод узловых потенциалов

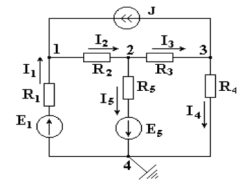
Этот метод позволяет уменьшить число совместно решаемых Ур-ий до зн-я (у-1), где у – число узлов. Основа: приминение I Зн Кирхгофа и заключ в следующем: Один из узлов в схеме цепи принимается базисным с нулевым потенциалом. Для ост-ых узлов сост-ем ур-е по I Зн Кирхгофа, выражая токи ветвей ч/з потенциалы узлов. Решением системы опред пот-лы узлов отн-но базисного, a затем опр токи ветвей по обобщенному закону Ома.

Пр. В схеме четыре узла.

Потенциал любой точки схемы можно принять равным нулю. Тогда у нас останутся неизвестными три потенциала. Узел, величину потенциала кот выбирают произвольно, наз базисным. Укажем в схеме произвольно направления токов. Примем для схемы φ4 = 0.

Запишем ур-ние по I Зн Кирхгофа д/узла 1.

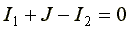(4.6)

В соответствии с законами Ома для активной и пассивной ветви

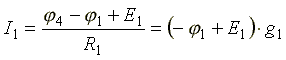где 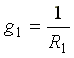- проводимость первой ветви.

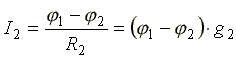, где - проводимость второй ветви.

Подставим выражения токов в уравнение (4.6).

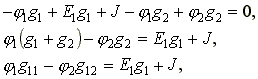(4.7)

где g11 = g1 + g2 - собственная проводимость узла 1.

Собственной проводимостью узла называется сумма проводимостей ветвей, сходящихся в данном узле.

g12 = g2 - общая проводимость между узлами 1 и 2.

Общей проводимостью называют проводимость ветви, соединяющей узлы 1 и 2.

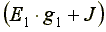- сумма токов источников, находящихся в ветвях, сходящихся в узле 1.

Если ток источника направлен к узлу, величина его записывается в правую часть уравнения со знаком "плюс", если от узла - со знаком "минус".

По аналогии запишем для узла 2:

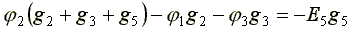(4.8)

для узла 3:

(4.9)

Решив совместно уравнения (4.7), (4.8), (4.9), определим неизвестные потенциалы φ1, φ2, φ3, а затем по закону Ома для активной или пассивной ветви найдем токи.

Если число узлов схемы - n, количество ур-ний по методу узловых потенциалов - (n - 1).

Дата добавления: 2015-05-06