Соединение потребителей звездой

Последовательное соедин активного сопрот и катушки индуктивности. Схема, ур-я напряжений, треуг напряжений. Векторная диаграмма.

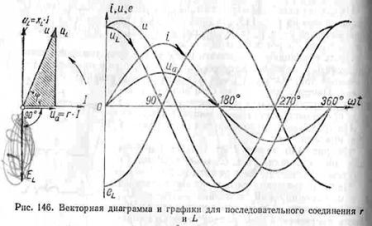
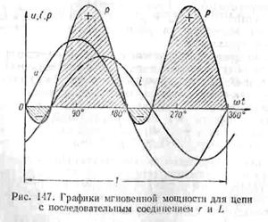
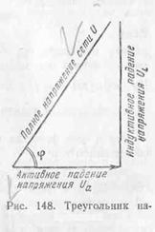Таким образом, средняя, или активная, мощность Р переменного тока зависит не только от величин напряжения U и тока I, но также и от сдвига фаз φ между ними. Активное падение напряжения определяется по формуле: Ua=I*r, индуктивное падение напряжения UL=I*XL, Полное падение напряжения равно напряжению сети:

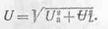
9. Последоват соедин активного и емкостного сопрот. Схема. Треуг напряж. Диаграмма.

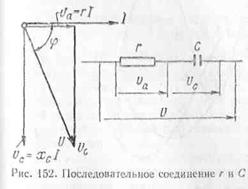
Из графика видно, что в течение некоторой части периода энергия затрачивается в цепи на нагрев сопротивления г и образование электрического поля (мощность положительная). В течение другой части периода энергия, накопленная в электрическом поле конденсатора, возвращается обратно в сеть.

Активное падение напряжения определяется по формуле: Ua=I*r, емкостное падение напряжения UС=I*XС, Полное падение напряжения равно напряжению сети: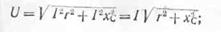

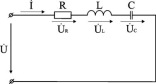10. Последоват соедин активного, емкостного и активно-индукт сопрот. Второй закон Кирхгофа для напряжений. Схема. Векторная диаграмма. Из свойства последовательного соединения следует, что ток во всех элементах цепи одинаковый. Напряжения на элементах определяются по формулам UR = I R, ψuR = ψi;

UL = I XL, ψuL = ψi + 90°;

UC = I XC, ψuC = ψi - 90°.

Для напряжений выполняется второй закон Кирхгофа в векторной форме Ú = ÚR + ÚL + ÚC.

В зависимости от величин L и С возможны следующие варианты: XL > XC; XL < XC; XL = XC. Для варианта XL > XC угол φ > 0, UL > UC. Ток отстает от напряжения на угол φ. Цепь имеет активно-индуктивный 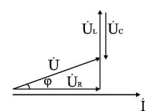характер. Векторная диаграмма напряжений имеет вид

Для варианта XL < XC угол φ < 0, UL < UC. Ток опережает напряжение на угол φ. Цепь имеет активно-емкостный характер. Векторная диаграмма напряжений имеет вид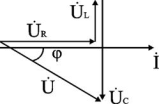

Для варианта XL = XC угол φ = 0, UL = UC. Ток совпадает с напряжением. Цепь имеет активный характер. Полное сопротивление z=R наименьшее из всех возможных значений XL и XC. Векторная диаграмма напряжений имеет вид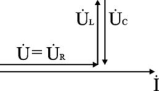

Этот режим называется резонанс напряжений (UL = UC). Напряжения на элементах UL и UC могут значительно превышать входное напряжение.

11. Резонанс напряж. Усл получ резонанса напряж. Общ сопрот, коэф мощн, велич тока и мощн при резонансе напряж.График и векторная диаграмма для резонанса напряжений выглядят след образом: Условием резонанса напряжений является равенство ХL =Xс. Поэтому резонанс напряжений в цепа с последовательным соединением r, L и С может наступить: 1) если при постоянной индуктивности емкость меняется и становится равной 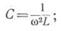2) если при постоянной емкости меняется индуктивность и становится равной 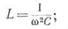3) если изменение обеих величин L и С приводит к равенству 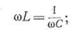4) если, наконец, угловая частота сети, изменяясь, становится равной 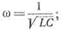Учитывая, что w= 2πf, получаем следующее выражение для частоты f0: 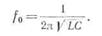Эту частоту принято называть резонансной.

Резонанс напряжений – это неприятное явление в электрических цепях, т.к. сопровождается повышением напряжения на L и C, которое может оказаться значительно выше Uвх. Это может вызвать пробой изоляции индуктивной катушки и конденсатора. В такой цепи Z=r. Ток в цепи по закону Ома будет равен I= Uвх/r=Imax. Поскольку при резонансе в цепи действует только активное сопротивление r, то φr=0, cosφ=1.Это значит что общее реактивное сопротивление X=XL-XC=0. Емкостное и индуктивное сопротивление компенсируют друг друга.

12. Параллельное соедин сопрот в цепи перемен тока. Схема. Общий ток и сдвиг фаз между током и напряж каждой цепи. Треуг токов. Активная, реактивная и полная мощн. Векторная диаграмма. Разветвленными цепями являются цепи, содержащие параллельные ветви.

I1=U/z1, z1=r1²+XL²

I2=U/z2, z2=r2²+XC²

Ip, Ip1, Ip2 – реактивная составляющая токов

Ia,Ia1,Ia2 – активные токи 1 и 2-ой ветвей и общ

Проводимость измеряется в Симменсах (Си)

Активные и реактивные составляющие тока можно выразить через сопротивление ветвей r1 и XL; r2 и XC и напряжение U по закону Ома.

I_a1=I1*cosφ1=U*r1/z²=U1*g1, где

g1= r1/z² - активная проводимость первой ветви

I_p1=I1*sinφ1=U*XL/z²=U1*b1, где

b1= XL/z² - реактивная проводимость первой ветви. Аналогично для второй ветви.

Для всей цепи:

Ia=Ia1+Ia2=Ug1+Ug2=U(g1+g2)=Ug

Ip=Ip1-Ip2=Ub1-Ub2=U(b1-b2)=Ub, где

g - активная проводимость всей цепи

b – реактивная проводимость всей цепи

Угол сдвига tgφ=bL-bC/g1+g2=b/g

Активная провоимость равна арифметической сумме проводимостей параллельных цепей. Реактивная проводимость равна алгебраической сумме проводимостей параллельных цепей.

Q=U*I*sinφ=QL-QC, QL>0, QC≤0

P=P1+P2=U*I*cosφ

S= 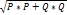=U*I

а) цепь с параллельным соединением R,L,C

б) треугольник токов

в) треугольник проводимостей

Общий ток в цепи будет иметь только активную составляющую и будет совпадать по фазе с напряжением(при резонансе токов).

IL/I=bL/g IC/I=bC/g, т.к. bL=bC, то IL=IC

13. Проводимости цепи переменного тока. Треуг провод. Коэф мощн. Выражения провод ч\з сопрот цепи. Активные и реактивные составляющие тока можно выразить через сопротивление ветвей r1 и XL; r2 и XC и напряжение U по закону Ома.

I_a1=I1*cosφ1=U*r1/z²=U1*g1, где

g1= r1/z² - активная проводимость первой ветви

I_p1=I1*sinφ1=U*XL/z²=U1*b1, где

b1= XL/z² - реактивная проводимость первой ветви. Аналогично для второй ветви.

Для всей цепи:

Ia=Ia1+Ia2=Ug1+Ug2=U(g1+g2)=Ug

Ip=Ip1-Ip2=Ub1-Ub2=U(b1-b2)=Ub, где

g - активная проводимость всей цепи

b – реактивная проводимость всей цепи

Угол сдвига tgφ=bL-bC/g1+g2=b/g

Активная провоимость равна арифметической сумме проводимостей параллельных цепей. Реактивная проводимость равна алгебраической сумме проводимостей параллельных цепей.

Q=U*I*sinφ=QL-QC, QL>0, QC≤0

P=P1+P2=U*I*cosφ

S= 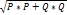=U*I

Коэффициент мощности — безразмерная физическая величина, показывает, насколько сдвигается по фазе переменный ток, протекающий через нагрузку, относительно приложенного к ней напряжения.

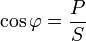
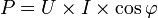
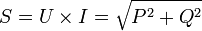
Здесь P — активная мощность,S — полная мощность, Q — реактивная мощность.

14. Повышение коэф мощн цепи. Схема. Векторная диаграмма. Расчет емкости для компенсации. Повышение коэффициента мощности на промышленных предприятиях.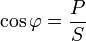

cosφ≈0,7÷0,8 - это значит, что предприятие потребляет из сети 70-80% активного тока, а 20-30% реактивного. Поскольку активный ток идет на получение полезной мощности, а реактивный ток никакой полезной работы не выполняет, а только сдвигает ток по отношению к U в магнитных цепях, поэтому государство заинтересовано в передаче только активного тока и заставляет предприятия повышать cosφ до 1, а активный ток = 100%. При этом полностью используются проводниковые материалы и получ повыш коэф КПД.

Для того чтобы увеличить cosφ требуется большая емкость (большое кол-во конденсаторов).

15. Резонанс токов. Условия получ резонанса токов. Общая проводимость, коэф мощности, величина тока и мощности при резонансе. Область примен резонансов. В цепи переменного тока, в которой индуктивность и емкость соединены параллельно может возникнуть резонанс токов при условии равенства токов в индуктивности IL и емкости IC. В результате резонанса токов общий ток в цепи может быть относительно мал, а в контуре индуктивности и емкости, где происходят электрические колебания, протекает переменный ток, значительно больший общего.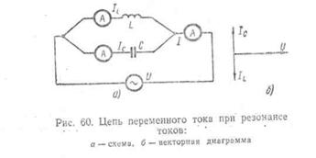

Известно, что при резонансе токов (при r = 0) индуктивное сопротивление равно емкостному и реактивные проводимости равны между собой. отсюда следует, что

Извлечем корень квадратный из этой величины. Тогда получим, что частота свободных электрических колебаний в контуре

где f—частота тока, гц

L — индуктивность, гн;

С — емкость, ф.

Из формулы (73) следует, что, изменяя величину емкости или индуктивности контура, можно изменять — регулировать частоту свободных колебаний, т, е. можно настраивать контур на определенную частоту. Как известно, чтобы в рассматриваемой цепи наступил резонанс токов, необходимо создать такие условия, при которых ток в индуктивности IL ток в емкости Iс были бы равны друг другу. Допустим, что подбором индуктивности и емкости или изменением частоты созданы условия для резонанса токов, т. е. На параллельно соединенных сопротивлениях ХL и Хс напряжение одинаково. Ток в индуктивности , а ток в емкости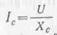

На векторной диаграмме видно, что ток в индуктивности и том в емкости сдвинуты по фазе на угол j=180о и равны друг другу. Отсюда следует, что общий ток при резонансе токов равен нулю, а полное сопротивление цепи бесконечно велико. В действительности общий ток будет относительно мал, но не равен нулю. Этот ток, который вырабатывает генератор, является активным и покрывает потери энергии в контуре. Резонанс применяется в приемниках, полосовых фильтрах, генераторах.

16. Электрич измерения, единицы измер. Классифик эектроизмерит приборов. ЭЛЕКТРИЧЕСКИЕ ИЗМЕРЕНИЯ - измерение электрических величин, таких, как напряжение, сопротивление, сила тока, мощность. Измерения производятся с помощью различных средств – измерительных приборов, схем и специальных устройств. Тип измерительного прибора зависит от вида и размера (диапазона значений) измеряемой величины, а также от требуемой точности измерения. В электрических измерениях используются основные единицы системы СИ: вольт (В), ом (Ом), фарада (Ф), генри (Г), ампер (А) и секунда (с). Значения единиц электрических величин определяются международным соглашением в соответствии с законами физики и единицами механических величин. Электрические измерения проводятся в соответствии с государственными эталонами единиц напряжения и силы постоянного тока, сопротивления постоянному току, индуктивности и емкости. Такие эталоны представляют собой устройства, имеющие стабильные электрические характеристики, или установки, в которых на основе некоего физического явления воспроизводится электрическая величина, вычисляемая по известным значениям фундаментальных физических констант. Эталоны ватта и ватт-часа не поддерживаются, так как более целесообразно вычислять значения этих единиц по определяющим уравнениям, связывающим их с единицами других величин. Электроизмерительные приборы чаще всего измеряют мгновенные значения либо электрических величин, либо неэлектрических, преобразованных в электрические. Все приборы делятся на аналоговые и цифровые. Первые обычно показывают значение измеряемой величины посредством стрелки, перемещающейся по шкале с делениями. Вторые снабжены цифровым дисплеем, который показывает измеренное значение величины в виде числа. Цифровые приборы в большинстве измерений более предпочтительны, так как они более точны, более удобны при снятии показаний и, в общем, более универсальны. Цифровые универсальные измерительные приборы («мультиметры») и цифровые вольтметры применяются для измерения со средней и высокой точностью сопротивления постоянному току, а также напряжения и силы переменного тока. Аналоговые приборы постепенно вытесняются цифровыми, хотя они еще находят применение там, где важна низкая стоимость и не нужна высокая точность. Для самых точных измерений сопротивления и полного сопротивления (импеданса) существуют измерительные мосты и другие специализированные измерители. Для регистрации хода изменения измеряемой величины во времени применяются регистрирующие приборы – ленточные самописцы и электронные осциллографы, аналоговые и цифровые.

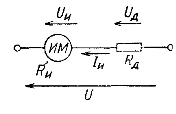
17. Шунты и добавочные сопрот для расширения переделов измерения токов и напряж. Измерительные шунты. Шунт является простейшим измерительным преобразователем тока в напряжение. Измерительный шунт представляет собой четырехзажимный резистор. Два входных зажима шунта, к которым подводится ток I, называются токовыми, а два выходных зажима, с которых снимается напряжение U, называются потенциальными. К потенциальным зажимам шунта обычно присоединяют измерительный механизм измерительного прибора. Измерительный шунт характеризуется номинальным значением входного тока Iном и номинальным значением выходного напряжения Uном. Их отношение определяет номинальное сопротивление шунта: Rш= Uном / Iном

Шунты применяются для расширения пределов измерения измерительных механизмов по току, при этом большую часть измеряемого тока пропускают через шунт, а меньшую — через измерительный механизм. Шунты имеют небольшое сопротивление и применяются, главным образом, в цепях постоянного тока с магнитоэлектрическими измерительными механизмами.

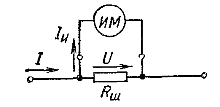
Добавочные резисторы. Добавочные резисторы являются измерительными преобразователями напряжения в ток, а на значение тока непосредственно реагируют измерительные механизмы вольтметров. Добавочные резисторы служат для расширения пределов измерения по напряжению вольтметров различных систем и других приборов, имеющих параллельные цепи, подключаемые к источнику напряжения. Сюда относятся, например, ваттметры, счетчики энергии, фазометры и т. д. Добавочный резистор включают последовательно с измерительным механизмом. Ток Iи в цепи, состоящий из измерительного механизма с сопротивлением Rи и добавочного резистора с сопротивлением Rд, составит:

Iи = U / (Rи + Rд),

где U — измеряемое напряжение.

Если вольтметр имеет предел измерения Uном и сопротивление измерительного механизма Rи и при помощи добавочного резистора Rд надо расширить предел измерения в n раз, то, учитывая постоянство тока Iи, протекающего через измерительный механизм вольтметра, можно записать:

Uном / Rи = n U ном / (Rи + Rд)

откуда

Rд = Rи (n - 1)

Добавочные резисторы бывают внутренние и наружные. Последние выполняются в виде отдельных блоков и подразделяются на индивидуальные и калиброванные. Индивидуальный резистор применяется только с тем прибором, который с ним градуировался. Калиброванный резистор может применяться с любым прибором, номинальный ток которого равен номинальному току добавочного резистора. Калиброванные добавочные резисторы делятся на классы точности 0,01; 0,02; 0,05; 0,1; 0,2; 0,5 и 1,0. Они выполняются на номинальные токи от 0,5 до 30 мА.

Добавочные резисторы применяются для преобразования напряжений до 30 кВ.

18. Трехфазн электрич цепи. Принцип получения трехфазного тока. Соединение фазовых обмоток генератора звездой. Векторная диаграмма. ЭДС. Трехфазная цепь является частным случаем многофазных электрических систем, представляющих собой совокупность электрических цепей, в которых действуют ЭДС одинаковой частоты, сдвинутые по фазе относительно друг друга на определенный угол. Каждую из частей многофазной системы, характеризующуюся одинаковым током, называют фазой, т.е. фаза – это участок цепи, относящийся к соответствующей обмотке генератора или трансформатора, линии и нагрузке. Источником трехфазного напряжения является трехфазный генератор, на статоре которого размещена трехфазная обмотка. Фазы этой обмотки располагаются таким образом, чтобы их магнитные оси были сдвинуты в пространстве друг относительно друга на 2π/3 эл. рад. При вращении ротора с равномерной скоростью в обмотках фаз статора индуцируются синусоидальные ЭДС одинаковой частоты и амплитуды, но отличающиеся друг от друга по фазе на 2π/3 рад. Векторная диаграмма для симметричной системы ЭДС, соответствующей трехфазной системе выглядит:

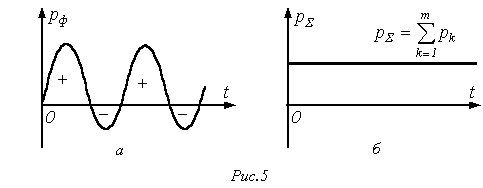
Все симметричные трех- и m-фазные (m>3) системы являются уравновешенными. Это означает, что хотя в отдельных фазах мгновенная мощность пульсирует (см. рис. 5,а), изменяя за время одного периода не только величину, но в общем случае и знак, суммарная мгновенная мощность всех фаз остается величиной постоянной в течение всего периода синусоидальной ЭДС (см. рис. 5,б).

Уравновешенность имеет важнейшее практическое значение. Если бы суммарная мгновенная мощность пульсировала, то на валу между турбиной и генератором действовал бы пульсирующий момент. Такая переменная механическая нагрузка вредно отражалась бы на энергогенерирующей установке, сокращая срок ее службы. Эти же соображения относятся и к многофазным электродвигателям.

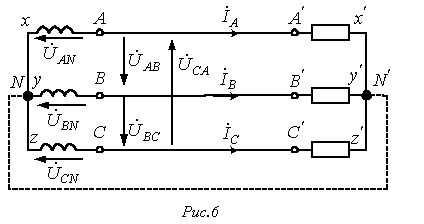
Для уменьшения количества проводов в линии фазы генератора гальванически связывают между собой. Различают два вида соединений: в звезду и в треугольник. В свою очередь при соединении в звезду система может быть трех- и четырехпроводной.

На рис. 6 приведена трехфазная система при соединении фаз генератора и нагрузки в звезду. Здесь провода АА’, ВВ’ и СС’ – линейные провода.

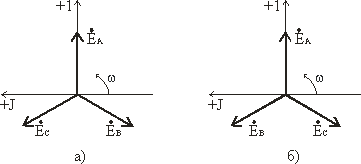
Векторная диаграмма трехфазной симметричной системы ЭДС показана на рис а)

19. Соедин звездой с нулевым проводом. Электрическая схема. Определение фазных и линейных токов и напряж; осн матем соотнош между ними. Топографич диаграмма. Провод, соединяющий нейтральные точки генератора и приемника, называется нейтральным (на рис. 6 показан пунктиром). Трехфазная система при соединении в звезду без нейтрального провода называется трехпроводной, с нейтральным проводом – четырехпроводной.

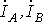Все величины, относящиеся к фазам, носят название фазных переменных, к линии - линейных. Как видно из схемы на рис. 6, при соединении в звезду линейные токи и 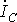равны соответствующим фазным токам. При наличии нейтрального провода ток в нейтральном проводе 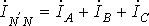. Поскольку напряжение на источнике противоположно направлению его ЭДС, фазные напряжения генератора (см. рис. 6) действуют от точек А,В и С к нейтральной точке N; 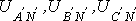- фазные напряжения нагрузки. Линейные напряжения действуют между линейными проводами. В соответствии со вторым законом Кирхгофа для линейных напряжений можно записать , , ,

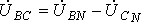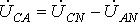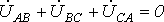
На рис. 7 представлена векторная диаграмма для симметричной системы напряжений. Как показывает ее анализ (лучи фазных напряжений образуют стороны равнобедренных треугольников с углами при основании, равными 300), в этом случае

Напряжение между линейным проводом и нейтралью (Ua, Ub, Uc) называется фазным. Напряжение между двумя линейными проводами(UAB, UBC, UCA) называется линейным. Для соединения обмоток звездой, при симметричной нагрузке, справедливо соотношение между линейными и фазными токами и напряжениями:

20. Представление лин напряж векторами фазных напряж. Определ числовых соотнош между лин и фазными напряж с помощью равнобедрен треуг из векторн диаграммы. Назначение нейтрального провода. Провод, соединяющий нейтральные точки генератора и приемника, называется нейтральным (на рис. 6 показан пунктиром). Трехфазная система при соединении в звезду без нейтрального провода называется трехпроводной, с нейтральным проводом – четырехпроводной.

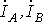Все величины, относящиеся к фазам, носят название фазных переменных, к линии - линейных. Как видно из схемы на рис. 6, при соединении в звезду линейные токи и 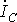равны соответствующим фазным токам. При наличии нейтрального провода ток в нейтральном проводе 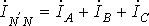. Поскольку напряжение на источнике противоположно направлению его ЭДС, фазные напряжения генератора (см. рис. 6) действуют от точек А,В и С к нейтральной точке N; 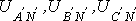- фазные напряжения нагрузки. Линейные напряжения действуют между линейными проводами. В соответствии со вторым законом Кирхгофа для линейных напряжений можно записать , , ,

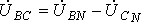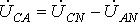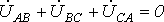
На рис. 7 представлена векторная диаграмма для симметричной системы напряжений. Как показывает ее анализ (лучи фазных напряжений образуют стороны равнобедренных треугольников с углами при основании, равными 300), в этом случае

Соединение нейтральных точек генератора и приёмника электроэнергии нейтральным проводом позволяет снизить напряжение смещения нейтрали (в случае, если к каждой фазе подключается разная нагрузка, в системе возникнет так называемое напряжение смещения нейтрали, которое вызовет несимметрию напряжений нагрузки) практически до нуля и выровнять фазные напряжения на приёмнике электроэнергии. Небольшое напряжение будет обусловлено только сопротивлением нулевого провода.

21. Соединение звездой без нулевого провода в трехвазн цепях. Схема. Векторная диаграмма для чисто активн нагрузки (сим нагрузка). При наличии нейтрального провода ток в нейтральном проводе 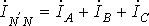. Если система фазных токов симметрична, то . Следовательно, если бы симметрия токов была гарантирована, то нейтральный провод был бы не нужен. Отсутствие нейтрального провода устраняет жёсткую привязку напряжения на нагрузке к напряжению источника питания, и в случае несимметричной нагрузки по фазам эти напряжения не равны между собой. В схеме звезда без нулевого провода в каждое мгновение ток по одному или двум проводам проходит от источника трехфазного тока к приемнику, а по двум другим или по одному протекает обратно от приемника к источнику.

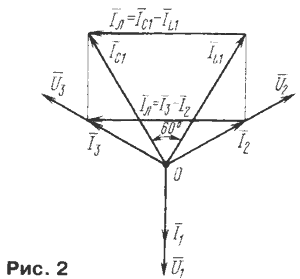
На рис. 2 приведена векторная диаграмма напряжений для устройства при чисто активной нагрузке R в каждой ветви.

22. Соедин звездой в трехфазн цепях без нулевого провода при несим нагрузке. Эл схема и векторн диаграмма. Определ напряж смещ. Выраж для фазн токов. Для определения фазных напряжений при несимметричной нагрузке, соединённой звездой без нейтрального провода, используют метод двух узлов. В соответствии с этим методом расчёт начинают с определения напряжения UN между нейтральными точками источника питания и нагрузки, называемого напряжением смещения нейтрали: 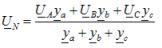где ya, yb, yc – полные проводимости соответствующих фаз нагрузки в комплексной форме

Напряжения на фазах несимметричной нагрузки находят из выражений: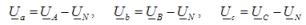

В частном случае несимметрии нагрузки, когда при отсутствии нейтрального провода происходит короткое замыкание одной из фаз нагрузки, напряжение смещения нейтрали равно фазному напряжению источника питания той фазы, в которой произошло короткое замыкание. Напряжение на замкнутой фазе нагрузки равно нулю, а на двух других оно численно равно линейному напряжению. Фазные токи в нагрузке, они же и токи линейных проводов при любом характере нагрузки:

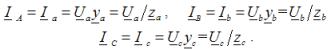
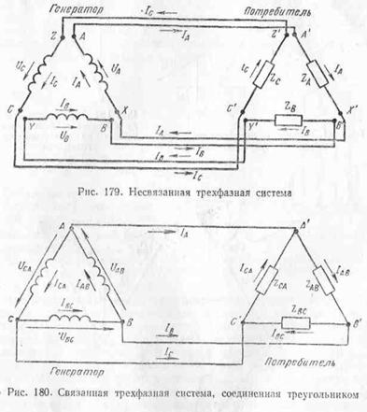23. Соедин потребит треугольником. Эл схема. Определ лин токов по фазн токам по 1 зак Кирхгофа для узлов A, B, C. Векторная диагр напряж и токов. Если обмотки генератора соединены треугольником, то, линейное напряжение создает каждая фазная обмотка. У потребителя, соединенного треугольником, линейное напряжение подключается к зажимам фазного сопротивления. Следовательно, при соединении треугольником фазное напряжение равно линейному Ua=Uф. Определим зависимость между фазными и линейными токами при соединении треугольником, если нагрузка фаз будет одинакова по величине и характеру.

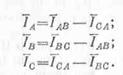Составляем уравнения токов по первому закону Кирхгофа для трех узловых точек А1, В1 и С1 потребителя: откуда

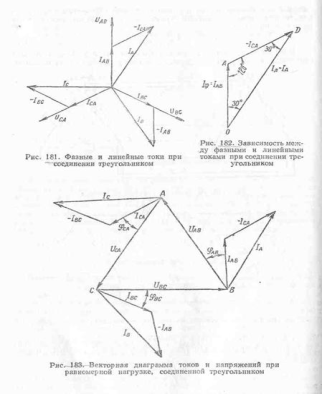Отсюда видно, что линейные токи равны геометрической разности фазных токов. При симметричной нагрузке фазные токи одинаковы по величине и сдвинуты один относительно другого на 120°. Производя вычитание векторов фазных токов согласно полученным уравнениям, получаем линейные токи (рис. 181). Зависимость между фазными и линейными токами при соединении в треугольник показана на рис. 182:

Следовательно, при симметричной нагрузке, соединенной треугольником, линейный ток в 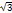раз больше фазного тока. На рис. 183 дана векторная диаграмма токов и напряжений при равномерной активно-индуктивной нагрузке, соединенной треугольником. Построение диаграммы производится следующим образом. В выбранном масштабе строим равносторонний треугольник линейных напряжений сети Uав, Ubc и Uас, которые равны фазным напряжениям потребителя. В сторону отставания под углами jAB, jBC, jCA к линейным напряжениям UAB, Uвс и Uса строим в масштабе векторы фазных токов IAB, IBC и ICA. Затем, как было указано раньше, определяем линейные токи IA, IB и IC. У двигателей и у других потребителей трехфазного тока в большинстве случаев наружу выводят все шесть концов трех обмоток, которые по желанию можно соединять либо звездой, либо треугольником. Обычно к трехфазной машине крепится доска из изоляционного материала (клеммная доска), на которую и выводят все шесть концов.

24. Определ мощностей в 3-фазн цепях при соедин звездой и треуг. Схемы включ и осн соотнош. В трехфазных цепях, так же как и в однофазных, пользуются понятиями активной, реактивной и полной мощностей.

В общем случае несимметричной нагрузки активная мощность трехфазного приемника равна сумме активных мощностей отдельных фаз

P = Pa + Pb + Pc, где

Pa = Ua Ia cos φa;

Pb = Ub Ib cos φb;

Pc = Uc Ic cos φc;

Ua, Ub, Uc; Ia, Ib, Ic – фазные напряжения и токи;

φa, φb, φc – углы сдвига фаз между напряжением и током.

Реактивная мощность соответственно равна алгебраической сумме реактивных мощностей отдельных фаз

Q = Qa + Qb + Qc, где

Qa = Ua Ia sin φa;

Qb = Ub Ib sin φb;

Qc = Uc Ic sin φc.

Полная мощность отдельных фаз

Sa = Ua Ia;

Sb = Ub Ib;

Sc = Uc Ic.

Полная мощность трехфазного приемника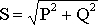

При симметричной системе напряжений (Ua = Ub = Uc = UФ) и симметричной нагрузке (Ia = Ib = Ic = IФ; φa = φb = φc = φ) фазные мощности равны Pa = Pb = Pc = PФ = UФ IФ cos φ; Qa = Qb = Qc = QФ = UФ IФ sin φ.

Активная мощность симметричного трехфазного приемника P = 3 PФ = 3 UФ IФ cos φ.

Аналогично выражается и реактивная мощность

Q = 3 QФ = 3 UФ IФ sin φ.

Полная мощность S = 3 SФ = 3 UФ IФ.

Отсюда следует, что в трехфазной цепи при симметричной системе напряжений и симметричной нагрузке достаточно измерить мощность одной фазы и утроить результат.

Дата добавления: 2015-05-06