Краткая теория

Задачи

Номер задачи соответствует номеру варианта

2.1 В результате случайного выборочного обследования 100 торговых киосков города получены следующие сводные данные о дневной выручке частного бизнеса:

Выручка от продажи товара, тыс. руб.	Число торговых киосков
До 100 100 – 120 120 – 140 140 – 160 160 – 180 180 – 200 200 и выше

Определить:

1) среднедневную выручку от продаж товаров;

2) среднее квадратическое отклонение и коэффициент вариации;

3) с вероятностью 0,954 ожидаемую выручку от продажи товаров частных торговых киосков города.

№2.2 Для изучения качества продукции из партии деталей в 1000 штук отобрано в механическом порядке 100 деталей. Средний диаметр обследованных деталей оказался равным 300 мм., а среднее квадратическое отклонение – 10 мм. Определите с вероятностью 0,997 пределы, в которых ожидается средний диаметр деталей во всей партии.

№ 2.3 На электроламповом заводе в порядке случайной выборки проверено 1600 ламп, из которых 48 оказались бракованными. Средняя продолжительность горения ламп равнялась 900 часам при среднеквадратическом отклонении, равном 50 часам.

С вероятностью 0,954 определите:

1) пределы, в которых находится процент бракованных ламп;

2) пределы, в которых находится средняя продолжительность горения ламп.

№2.4 В цехе 1000 человек. С целью определения затрат времени рабочими на изготовление одной детали необходимо провести выборочное обследование рабочих методом механического отбора. Предварительным обследованием установлено, что среднее квадратическое отклонение затрат рабочего времени на изготовление одной детали составило 5 мин.

Определите, какое число рабочих необходимо отобрать, чтобы с вероятностью 0,954 ошибка выборки не превышала 1 минуты.

№2.5 В городе 40 000 семей методом случайного бесповторного отбора было обследовано 3000 семей. В результате обследования было установлено, что 1000 семей являются владельцами акций.

С вероятностью 0,997 определите пределы, в которых будет находитЬся доля семей, имеющих акции в городе.

№2.6 В целях изучения норм расходования сырья на единицу продукции проведена 2–процентная механическая выборка партии изделий, в результате чего получены следующие данные:

Все изделия, г.	Число изделий, шт.
До 200 200 – 205 205 – 210 210 – 215 свыше 215
Итого

По данным обследования определите:

1) средний вес изделия: дисперсию и среднее квадратическое отклонение; коэффициент вариации;

2) с вероятностью 0,954 возможные пределы: а) среднего веса изделия во всей партии изделий; б) удельного веса изделий с расходом сырья на единицу продукции от 205 до 210 г.

№ 2.7 Из партии 4000 деталей отобрано 1000 деталей. Среди отобранных деталей 2% оказались бракованными. С какой вероятностью можно утверждать, что вся партия содержит не более 2,5 % брака.

№2.8 Из партии готовой продукции методом случайного отбора отобрано 250 изделий, из которых 5 оказались бракованными.

Определите с вероятностью 0,954 возможные пределы процента брака во всей партии.

№2.9 Средний вес изделия в выборочной совокупности, состоящей из 100 единиц, оказался 5 кг. при среднем квадратическом отклонении 0,5 кг. С какой вероятностью можно утверждать, что вес изделия во всей партии не превысит 5,1 кг.

№2.10 Сколько деталей нужно отобрать из 1000 штук для определения одного из ее параметров, чтобы с вероятностью 0,954 можно было бы утверждать, что ошибка выборки не превысит 1,0 мм. Среднее квадратическое отклонение признака-6 мм.

Практическое задание №3. Регрессионный и корреляционный анализ

Корреляционно-регрессионный анализ как общее понятие включает в себя измерение тесноты, направления связи и установление аналитического выражения (формы) связи.

Корреляционный анализ имеет своей задачей количественное определение тесноты связи между двумя признаками (при парной связи) и между результативным и множеством факторных признаков (при многофакторной связи).

Регрессионный анализ заключается в определении аналитического выражения связи, в котором изменение результативного признака у обусловлено изменением факторных признаков, а множество всех прочих факторов, также оказывающих влияние на результативный признак, принимается за постоянные и средние значения.

Целью регрессионного анализа является оценка функциональной зависимости условного среднего значения результативного признака (у) от факторных ().

Регрессия может быть парной (однофакторной) и множественной (многофакторной). По форме зависимости – линейной и нелинейной, по направлению – прямой (положительной) и обратной (отрицательной).

Основной предпосылкой применения корреляционного анализа является необходимость подчинения совокупности значений всех факторных ()и результативного (у) признаков к- мерному нормальному закону распределения или близость к нему.

Это условие связано с применением метода наименьших квадратов при расчете параметров корреляционного уравнения: только при нормальном распределении метод наименьших квадратов дает оценку параметров, отвечающую принципам максимального правдоподобия. На практике эта предпосылка чаще всего выполняется приблизительно, но и тогда метод наименьших квадратов дает неплохие результаты.

Основной предпосылкой применения регрессионного анализа является то, что только результативный признак (у) подчиняется нормальному закону распределения, а факторные признаки () могут иметь произвольный закон распределения.

Уравнение регрессии или модель регрессии, выражаемая функцией

(),

будет достаточно адекватной реальному моделируемому явлению или процессу в случае соблюдения следующих требований их построения:

1. Совокупность исследуемых исходных данных должна быть однородной и описываться непрерывными функциями.

2. Моделируемые явления должны оцениваться одним или несколькими уравнениями причинно-следственных связей.

3. Все признаки должны иметь количественное (цифровое) выражение.

4. Наличие достаточно большого объема исследуемой выборочной совокупности. Обычно считают, что число наблюдений должно быть не менее чем в 5-6, а лучше – не менее чем в 10 раз больше числа факторов. Еще лучше, если число наблюдений в несколько десятков или в сотни раз больше числа факторов, тогда закон больших чисел, действует в полную силу, обеспечивает эффективное взаимопогашение случайных отклонений от закономерного характера связи признаков.

5. Отсутствие количественных ограничений на параметры модели связи.

Теоретическая обоснованность моделей взаимосвязи, построенных на основе корреляционно-регрессионного анализа, обеспечивается соблюдением следующих основных условий:

1. Все признаки и их совместные распределения должны подчиняться нормальному закону распределения.

2. Дисперсия моделируемого признака у должна все время оставаться постоянной при изменении величины у и значений факторных признаков.

3. Отдельные наблюдения моделируемого признака у должны быть независимыми, т.е. результаты, полученные в i-ом наблюдении, не должны быть связаны с предыдущими и содержать информацию о последующих наблюдениях, а также влиять на них.

Отступление от выполнения этих условий и предпосылок приводит к тому, что модель регрессии будет неадекватно отражать реально существующие связи между анализируемыми признаками.

Одной из проблем построения модели регрессии является ее размерность, т.е. определение числа факторных признаков, включаемых в модель. Их число должно быть оптимальным.

Сокращение размерности за счет исключения второстепенных, несущественных факторов (эта задача решается в основном на базе мер тесноты связи факторов с результативным признаком) позволяет получить модель, реализуемую быстрее и качественнее. В то же время построение модели малой размерности может привести к тому, что она будет недостаточно полно описывать исследуемое явление или процесс. Практика выработала определенный критерий, позволяющий установить оптимальное соотношение между числом факторных признаков, включаемых в модель, и объемом исследуемой совокупности. Согласно данному критерию число факторных признаков х должно быть 5-6 раз меньше объема изучаемой совокупности.

Построение корреляционно-регрессионных моделей, какими бы сложными они не были, само по себе не вскрывает полностью всех причинно-следственных связей. Основой их адекватности является предварительный качественный анализ, основанный на учете специфики и особенностей сущности исследуемых социально-экономических явлений и процессов.

Парная регрессия характеризует связь между двумя признаками: результативным и факторным.

Процесс построения модели парной регрессии включает следующие основные этапы:

1) выбор формы связи;

2) определение параметров уравнения связи и проверка адекватности регрессионной модели;

3) измерение тесноты связи и проверка значимости (надежности) показателей тесноты связи.

Выбор формы связи имеет решающее значение в корреляционно-регрессионном анализе. Все дальнейшие самые тщательные расчеты могут быть обесценены, если форма связи избрана неверно.

При выборе формы уравнения регрессии качественный анализ играет важную роль для раскрытия механизма формирования корреляционной связи. Пусть, например, измеряется связь между сроком сева и урожайностью. Чрезмерно ранний и чрезмерно поздний сев ведут к снижению урожайности, максимум которой достигается при севе в оптимальные сроки. Таким образом, с ростом факторного признака (срок сева) урожайность растет, а затем снижается. Зависимость такого рода может быть выражена, например, уравнением параболы.

При всей важности теоретического анализа следует, однако, учитывать, что социально-экономические явления очень сложны. Как правило, мы не имеем о них исчерпывающей информации, а внутренняя логика их связей мало изучена. Факторы, влияющие на то или иное явление, взаимно переплетаются и взаимодействуют друг с другом. Поэтому очень часто не удается сделать теоретически обоснованный вывод уравнения регрессии, т.е. формы связи, внутренне присущей изучаемому явлению. В ряде случаев на основе теоретического анализа могут быть высказаны лишь более или менее обоснованные предположения о том, что следует ожидать линейную или какую-либо нелинейную (криволинейную) связь, имеет ли ожидаемая криволинейная функция экстремальные значения и т.п. Так, в рассмотренном примере можно утверждать, что линия регрессии – некоторая кривая, имеющая оптимум, но это отнюдь не обязательно парабола. Более того, если явление мало изучено, иногда могут быть выдвинуты и различные гипотезы о механизме и форме взаимосвязи.

Для проверки этих предположений и гипотез может быть использован графический метод – построение графика групповых средних, полученных в процессе аналитической группировки. Ломаная линия, изображающая изменение групповых средних результативного признака ( ) в зависимости от изменения группировочного фактора, называется эмпирической линией регрессии (эмпирической регрессией).

Наглядное представление о форме линии регрессии может дать график эмпирической линии регрессии (рис. 3,1).

Если эмпирическая линия по своему виду приближается к прямой линии, это свидетельствует о наличии прямолинейной корреляционной связи между признаками. Если же эмпирическая линия связи будет приближаться к кривой (параболе, гиперболе, показательной кривой), то это дает основание считать, что в данном случае имеется

криволинейная корреляционная связь, чем сильнее связь между признаками, тем теснее будут группироваться точки вокруг эмпирической линии регрессии.

В нашем примере можно предположить, что имеется прямая, прямолинейная сильная корреляционная зависимость между объемом собственных средств и привлеченными средствами.

Форма эмпирической линии регрессии дает возможность проверить, соответствует ли фактическое соотношение признаков тому или иному теоретически предполагаемому их соотношению. При этом нужно, однако, иметь, в виду, что при относительно небольшом числе единиц совокупности (числе наблюдения) форма эмпирической линии регрессии может изменяться при изменении число групп и их границ. Поэтому при небольшом числе наблюдений нельзя слишком полагаться на форму эмпирической линии регрессии, графический метод в таких случаях может оказаться недостаточно надежным.

Существуют более общие указания, позволяющие выявить уравнение связи, не прибегая к графическому изображению. Если результативный и факторный признаки возрастают одинаково, примерно в арифметической прогрессии, то это свидетельствует о том, что связь между ними линейная, а при обратной связи – гиперболическая.

Если факторный признак увеличивается в арифметической прогрессии, а результативный – значительно быстрее, то используется параболическая или степенная регрессия.

Если относительно формы связи могут быть выдвинуты разные теоретические гипотезы, а по виду эмпирической регрессии трудно судить о том, какой из этих гипотез наиболее соответствуют фактические данные, то в этих случаях строятся и решаются уравнения регрессии с различными формами связи, а затем с помощью специальных статистико-математических критериев оценивается их адекватность и выбирается та форма связи, которая обеспечивает наилучшую аппроксимацию (приближение) и достаточную статистическую достоверность и надежность.

Определение параметров уравнения связи и их значимости.

Аналитическая связь между факторным и результативным признаками описываются уравнениями:

прямой - ;

гиперболы - ;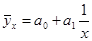

параболы - и т.д.

Выбрав тем или иным путем форму связи и построив уравнение регрессии в общем виде, необходимо далее найти числовые значения его параметров.

Оценка параметров уравнения осуществляется методом наименьших квадратов, в основе которого лежит предположение о независимости наблюдений исследуемой совокупности.

Сущность метода наименьших квадратов заключается в нахождении параметров модели (а_0, ,а₁), при которых минимизируется сумма квадратов отклонений эмпирических (фактических) значений результативного признака от теоретических, полученных по выбранному уравнению регрессии:

.

Для прямолинейной зависимости:

.

Рассматривая f в качестве функции а_0, и а₁ и проводя математические преобразования (дифференцирование), получаем:

;

.

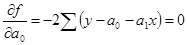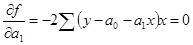Откуда система нормальных уравнений для нахождения параметров линейной полной регрессии имеет следующий вид:

.

Решение этой системы в общем виде дает следующие значения параметров:

Иногда их удобно исчислить по следующим формулам, дающим тот же результат:

где

или

; .

Определив значения а_0, и а₁ и подставив их в уравнение , находим значения , зависящие только от заданного значения х.

Корреляционное уравнение по форме похоже на уравнение функциональной зависимости, но по существу отличается тем, что оно справедливо лишь для совокупности, а не для отдельных явлений и зависит от объема совокупности (чем она больше, тем параметры уравнения типичнее).

В уравнении прямой параметр 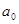экономического смысла не имеет. Параметр является коэффициентом регрессии и показывает изменение результативного признака при изменении факторного признака на единицу.

Широкое применение линейных уравнений объясняется в значительной мере тем, что зачастую значения признака х в изучаемой совокупности варьируют в весьма узких пределах. Если кривизна линии регрессии невелика, то в этих пределах отрезок кривой может быть достаточно точно описан уравнением прямой.

Кроме того, многие нелинейные функции (степенная, показательная, гипербола, парабола второго порядка) путем логарифмирования или замены переменных преобразуют в линейную форму.

Дата добавления: 2015-03-29