III способ

II способ.

I способ.

Решаем систему нормальных уравнений в следующей последовательности:

Домножим каждый член первого уравнения на 5

,

вычтем из второго уравнения первое и получим

, откуда .

Подставим значение 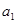в первое уравнение

,

получим 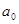=2,02.

Уравнение корреляционной связи примет вид

.

Параметры уравнения регрессии можно определять по формулам:

,

.

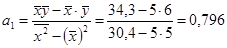, где ; ; .

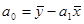Для определения параметров этим способом строим расчетную таблицу 3.6:

Таблица 3.6

№ предприятия	х	у
			-3 -2 -3 -1 -1		-3 -2 -1
Итого

;

.

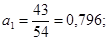
Корреляционное уравнение .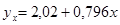

После определения параметров уравнения регрессии рассчитываем теоретическую линию регрессии путем подстановки значений х в уравнение корреляционной связи:

;

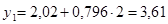, и т.д.

Если параметры уравнения связи определены правильно, то .

Окончательная проверка правильности расчета параметров уравнения связи производится подстановкой 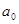и в систему нормальных уравнений.

Используя уравнение связи можно определить теоретическое значение для любой промежуточной точки (теоретическое значение выпуска готовой продукции на 1 работающего для любого промежуточного значения электровооруженности труда).

Коэффициент регрессии уточняет связь между х и у. Он показывает, на сколько единиц увеличивается результативный признак при увеличении факторного признака на единицу. В нашем примере =0,796. Значит, при увеличении электровооруженности труда на 1 работающего на 1 кВт. ч. выпуск продукции увеличится на 0,796 тыс. руб.

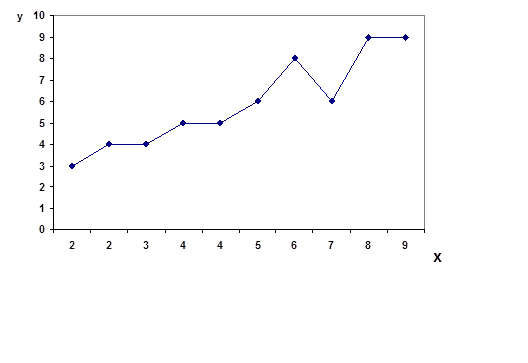Построим эмпирическую и теоретическую линии регрессии на графике:

Рис. 3.2 Зависимость выпуска готовой продукции на 1 работающего от электровооруженности труда

эмпирическая линия регрессии

теоретическая линия регрессии

При линейной зависимости между признаками для определения тесноты корреляционной связи применяются коэффициент корреляции (r) и индекс корреляции (R)

Наиболее удобной формулой для расчета коэффициента корреляции является следующая:

1) ,

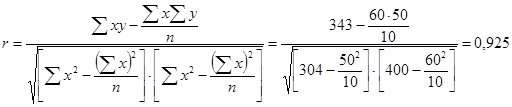r изменяется от – 1 до +1 и показывает тесноту и направление корреляционной связи. В нашем примере r=0,925, что показывает весьма тесную прямую связь между электровооруженностью труда рабочих и их производительностью труда.

Коэффициент корреляции можно рассчитывать и по другим формулам:

2) ,

где

3) .

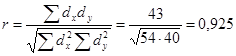4) если определена форма корреляционной связи и вычислен коэффициент регрессии , линейный коэффициент можно определить, используя формулу:

.

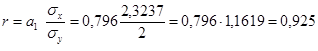5) Индекс корреляции удобно рассчитать по формуле:

,

- остаточная дисперсия характеризующая вариацию результативного признака от всех прочих, кроме х, факторов, определяется

;

- общая дисперсия, отображающая совокупное влияние всех факторов:

;

.

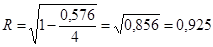По абсолютной величине линейный коэффициент корреляции r и индекс корреляции R при прямолинейной связи совпадают.

Дата добавления: 2015-03-29