Способы изображения периодических

Причины возникновения несинусоидальных токов.

Электрические цепи несинусоидального тока.

Периодическими несинусоидальными величинами называются любые электрические величины, которые изменяются во времени по периодическому несинусоидальному закону.

Источников энергии с абсолютно постоянными или синусоидальными ЭДС, строго говоря, не существует. Но если отклонения от постоянства или синусоидальности малы, то они не учитываются. В тех случаях, когда эти отклонения значительны, рассмотренные в разделах 1 и 2 методы анализа цепей применять нельзя.

Причинами возникновения несинусоидальных токов являются:

1. Несовершенство источников постоянных или синусоидальных ЭДС;

2. Подключение к электрической цепи источников несинусоидальных напряжений специальной формы. В практике самыми распространенными источниками такого типа являются релаксационные генераторы пилообразного напряжения. В промышленной электронике используются и другие типы релаксационных генераторов – мультивибраторы, которые создают напряжения пилообразной формы;

3. Нелинейные элементы, включаемые в цепь синусоидального тока. Наиболее распространенными цепями такого рода являются цепи, содержащие полупроводниковые диоды.

несинусоидальных величин.

Существует два способа изображения:

1. Графический – наиболее наглядный способ, когда в прямоугольной системе координат строятся графики мгновенных значений величин в зависимости от времени;

2. Аналитический – заключается в разложении периодических несинусоидальных функций в ряд Фурье, который состоит из постоянной, не зависящей от времени, составляющей и бесконечного числа гармонических составляющих, называемых гармониками.

В практических расчетах редко используют более пяти членов ряда Фурье. В общем случае периодическое несинусоидальное напряжение можно представить следующим рядом:

,

(5.1)

где U₀ – постоянная составляющая;

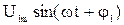– первая или основная гармоника, которая имеет период 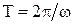и, который равен периоду несинусоидального напряжения;

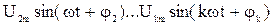– высшие гармоники;

U_1m U_Km – амплитуды гармоник;

φ₁ φ_К – начальные фазы гармоник.

Конкретный вид ряда Фурье для большинства периодических несинусоидальных напряжений используемых в электротехнике можно найти в соответствующих справочниках по математике.

Для характеристики содержания переменной составляющей в несинусоидальной величине служит коэффициент пульсаций:

.

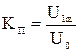(5.2)

Амплитуды и начальные фазы гармоник определяют спектральный состав несинусоидальной кривой, который задается в виде диаграмм амплитудно-частотного и фазо-частотного спектров (рис. 5.1 и 5.2).

На диаграмме амплитудно-частотного спектра откладывают относительные значения постоянной составляющей, а также относительные значения амплитуд гармоник.

Дата добавления: 2015-05-06