Системы счисления. Любая информация, даже литературная, может быть выражена в цифровом виде

Любая информация, даже литературная, может быть выражена в цифровом виде. Элементом цифровой информации является бит – это элементарная условная ячейка, которая содержит либо 0, либо 1. Эти цифры называют логическим нулем и логической единицей.

Все системы счисления дискретны и использует разрядный принцип обозначения числа:

Старший разряд

-----------

------------

------------

Младший разряд

Каждый разряд содержит число, равное цифре, умноженной на основание системы счисления.

Например, в десятичной системе число 17563 в поразрядном представлении имеет вид

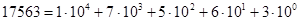
Число в любой системе записывается как последовательная запись цифр разрядов без множителей оснований в степени. Степень является одновременно указанием разряда: нулевой, первый и т.д. Иногда для указания системы счисления у числа ставится нижний индекс основания: 235₈.

Наиболее распространенными системами счисления являются двоичная (основание содержит две цифры – 0 и 1), восьмиричная (основание состоит из 8 цифр), десятичная, двенадцатиричная (исчисление времени), шестнадцатиричная, шестидесятиричная (исчисление времени) и др.

Двоичная система. В двоичной системе число записывается в виде последовательно расположенных 1 и 0, например: 1101100101₂. В поразрядной записи оно выглядит следующим образом:

1×2^9

1×2^8

0×2^7

1×2^6

1×2^5

0×2^4

0×2^3

1×2^2

0×2^1

1×2^0

Такая форма позволяет перевести двоичное число в десятичное посредством сложения чисел всех разрядов:

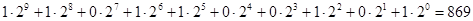
Чтобы перевести число из десятичной системы счисления в двоичную, необходимо выполнить следующие действия. Десятичное число, например 869, делят на 2 без десятичной дроби: 869/2=434 и 1 в остатке. Затем делится 434 на 2, в результате чего получаем число 217 без остатка, т.е. в остатке 0. Последующее деление даст результаты: 108 с остатком 1; 54 с остатком 0; 27 с остатком 0; 13 с остатком 1; 6 с остатком 1; 3 с остатком 0; 1 с остатком 1; и наконец, последняя 1 не делится на 2 и она занимает последний разряд. Таким образом, получилось от последних цифр (старший разряд) до первой (младший разряд): 1101100101.

Двоичная система является основной в цифровой технике, так как ее легко реализовать с помощью электронных элементов, имеющих два состояния: отсутствие сигнала на выходе (или низкий уровень) интерпретируется как логический 0, а высокий уровень напряжения на выходе как логическая 1.

Основными действиями с двоичными числами в цифровой электронике являются сложение и вычитание. Сложение и вычитание двух чисел в двоичном отображении производится следующим образом

-

+

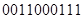
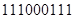
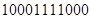
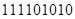
Сложение начинается с младших разрядов. Если складываются две единицы, то в младший разряд записывается 0, а в следующий, более старший разряд, разряд переносится 1. Если в нем 0, то эта 1 отображается в этом разряде. Если там 1, то в разряде остается 0, а единица переносится в следующий более высокий разряд. И так далее.

Вычитание также начинается с младшего разряда. Если в необходимом разряде нужна 1, она занимается из более старшего разряда. В нем соответственно изменяется содержание. Вычитание из нуля приводит к появлению 1 в разряде, в котором производится действие. Если в более старшем разряде был 0, то в нем остается 1, если была 1, то появляется 0.

Восьмеричная система. Основанием этой системы является число 8: 0,1, 2…7. В поразрядной записи, например десятичное число 10363 выглядит следующим образом

2×8^4

4×8^3

1×8^2

7×8^1

3×8^0

а его восьмеричный эквивалент – 24173₈.

Перевод десятичного числа в восьмеричное производится подобно тому, как это делается при переводе десятичного числа в двоичное. Остатки деления – это цифры в соответствующих разрядах, умноженные на основание в соответствующей степени разряда.

Шестнадцатеричная система счисления. Шестнадцатеричная система счисления имеет в основании число 16 – 0, 1, 2…9, A, B, C, D, E, F. Запись десятичного числа 890 в шестнадцатеричной системе выглядит следующим образом: 37Аh. Буква h в конце числа обозначает его принадлежность к шестнадцатеричной системе. Если шестнадцатеричное число начинается с буквы, то перед старшим разрядом записывается 0. Например 0Е43h.

Как правило, коды информации, обрабатываемые цифровыми устройствами, представляют собой двоичные числа, состоящие из 8 разрядов. Такой код называется байтом или словом. Восьмиразрядное слово можно представить в виде двух тетрад, шестнадцатиразрядное – в виде четырех тетрад. В этом случае возможно представление десятичного числа в виде нескольких тетрад, например

1000 0101 1001 0010

Этой записи соответствует десятичное число 8593.

Восьмиразрядная запись слова позволяет в памяти ЭВМ хранить буквенно-цифровые и символьные коды в количестве 256 единиц. Это обеспечивает возможность ввода с клавиатуры русского и иностранного алфавита, цифр, знаков и символов.

Дата добавления: 2015-05-06