Электрическая цепь с нелинейным индуктивным элементом

Нелинейными индуктивными элементами считаются катушки, намотанные на сердечник из ферромагнитного материала. На рис. 93 а показана катушка со стальным сердечником. Ее

а б

Рис.93

называют дросселем.

Индуктивность катушки. Индуктивное сопротивление таких катушек непостоянно и зависит от величины переменного тока.

𝑋_𝐿.= 𝜔𝐿; . (8-1)

Так как катушка содержит стальной сердечник, в котором концентрируется весь магнитный поток, то магнитная проницаемость ферромагнитного материала

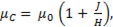(8-2)

где J-намагниченность тела.

Таким образом, вследствие изменения тока в цепи изменяется напряженность магнитного поля, которая приводит к изменению намагниченности ферромагнитного материала, т.е. изменению его магнитной проницаемости. С изменением же магнитной проницаемости меняется индуктивность дросселя, а следовательно, и его индуктивное сопротивление.

Индуктивность дросселя непостоянна, и магнитный поток в сердечнике в зависимости от тока в обмотке (вебер – амперная характеристика Ф = f(I)) имеет нелинейную кривую, подобную кривой намагничивания В= f(H).

Магнитный поток. Рассмотрим идеализированную катушку со стальным сердечником, т.е. катушку, в которой нет активного сопротивления, отсутствуют потоки рассеяния и потери в стали. Подведем к зажимам катушки синусоидальное напряжение 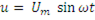. По обмотке начинает протекать переменный ток. В результате в витках катушки возникает эдс самоиндукции. Согласно второго закона Кирхгофа

(8-3)

Поскольку 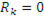, то

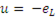. (8-4)

Видно, что напряжение и эдс находятся в противофазе, т.е. для любого момента времени переменное напряжение на концах обмотки уравновешивается эдс самоиндукции.

Согласно, закона Фарадея

(8-5)

где N – число витков катушки.

Тогда

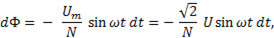
где действующее значение напряжения.

Интегрируем последнее выражение

(8-6)

где

амплитудное значение магнитного потока

U/ πʋN (8-7)

или

U = E = 4,44 (8-8)

- это соотношение называют уравнением трансформаторных эдс.

Таким образом, синусоидальное напряжение, приложенное к концам катушки со стальным сердечником создает синусоидальный магнитный поток в сердечнике катушки, который сдвинут по фазе на угол . Этот поток индуцирует в обмотке эдс, отстающую от него по фазе на на четверть периода (рис 93 б).

Ток в катушке. Для идеализированной катушки со стальным сердечником построим график i = f(t). Исходными являются функци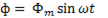и и .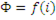

Кривую изменения тока i = f(t) строим графическим методом при условии, что намагничивание и размагничивание катушки происходит по одной и той же кривой, т.е. отсутствуют потери в стали.

Рис. 94

Для произвольного момента времени t₁ (точка 1) по кривой Ф (t) определяем магнитный поток Ф₁ (точка 2), после чего проектируем эту точку на график Ф(i) (точка 3) и по нему определяем значение тока i₁ (точка 4), соответствующего моменту времени t₁. Таким образом, получена первая точка искомой функции i(t). Проделав то же для других моментов времени, можно получить ряд точек функции i(t).

На рис. построен график i(t) без учета потерь в стали. Полученная кривая несинусоидальна. Кривая i(t) симметрична относительно оси абсцисс. Если же вести построение кривой i(t) с учетом потерь в стали, то она будет не только несинусоидальной, но и не симметричной.

Потери в стали. При прохождении переменного тока в катушке с ферромагнитным сердечником создается переменный магнитный поток. Магнитный поток концентрируется в стальном сердечнике, что приводит к его постоянному перемагничиванию. Процесс циклического перемагничивания ферромагнитного сердечника характеризуется петлей гистерезиса. Энергия, затрачиваемая на перемагничивание, превращается в тепловую, и сердечник нагревается.

Потери мощности в стальном сердечнике, состоят из потерь на гистерезис и потерь на вихревые токи:

. (8-9)

Потери на гистерезис можно сравнить с потерями на трение – под воздействием переменного магнитного поля магнитные домены, подобные миниатюрным магнитам, должны изменять свое направление, преодолевая силы внутреннего сцепления в ферромагнетике. Эти потери за один цикл перемагничивания пропорциональны площади петли гистерезиса материала сердечника. Чем более магнитотвердым является ферромагнетик (чем шире петля гистерезиса), тем больше потери на гистерезис.

Справочная литература рекомендует определять потери на гистерезис по формуле

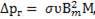(8-10)

где 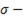коэффициент, зависящий от структуры материала; частота переменного тока − максимальная магнитная индукция; масса сердечника.

Потери на вихревые токи. При изменении магнитного потока, пронизывающего сердечник, в нем индуцируются вихревые токи, замыкающиеся в плоскостях, перпендикулярных к вектору магнитной индукции (рис. 95а).

а б

Рис. 95

Вихревые токи вызывают нагрев массивного стального сердечника, снижая кпд электрических машин, трансформаторов и других электромагнитных устройств. Кроме того, вихревые токи, согласно закона Ленца, оказывают размагничивающее действие, уменьшая основное магнитное поле катушки.

Для уменьшения вихревых токов стальные сердечники набираются из отдельных стальных листов толщиной 0,3-0,5мм, изолированных друг от друга тонкой бумагой или лаком (рис. 95б).

Потери на вихревые токи оцениваются по эмпирической формуле

(8-11)

где - коэффициент пропорциональности, зависящий от материала и толщины листов сердечника.

Дата добавления: 2015-05-06