Резонанс напряжений

Явление совпадения по фазе напряжения и тока в R, L, C -цепи называется электрическим резонансом.

В цепях переменного тока с последовательным соединением R, L, C - элементов при равенстве 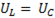возникает резонанс напряжений.

При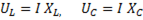

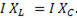
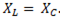
т.е. резонанс напряжений наступает при равенстве реактивных сопротивлений.

Условием резонанса напряжений является равенство

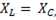(6-43)

или

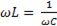(6-44)

Поэтому в цепи переменного тока резонанс напряжений может наступить:

1) если при постоянных L и C частота сигнала, подаваемого в цепь, изменяясь, становится равной ν = = ; ()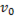

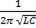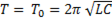2) если при постоянной частоте входного сигнала и постоянной индуктивности емкость конденсатора меняется и становится равной: С = ;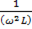

3) если при постоянной частоте входного сигнала и постоянной емкости меняется индуктивность и становится равной: L = ;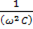

4) если при постоянной частоте входного сигнала изменение обеих величин L и C приводит к равенству: .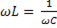

Таким образом, чтобы в цепи наступил резонанс напряжений, необходимо обеспечить определенное соотношение между величинами ν, L, C, т.е. резонанса в цепи можно добиться путем регулирования (подбора) параметров индуктивного и емкостного элементов, а также с помощью изменения частоты питающего тока. При резонансе частота тока (напряжения) равна частоте собственных колебаний цепи (контура).

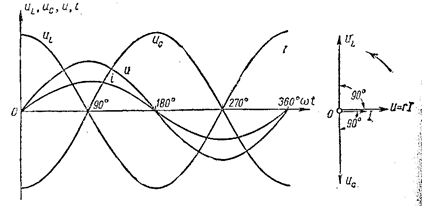
Рис. 77 Графики и векторная диаграмма для резонанса напряжений.

При резонансе напряжений выражение

U = = 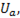(6-45)

так как .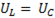

Полное сопротивление цепи

Z = 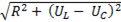= R, (6-46)

так как = .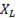

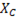Полная мощность цепи

S = 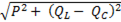= P, (6-47)

так как .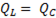

Фазовый сдвиг между током и напряжением

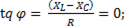(6-48)

так как 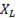= 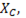следовательно .

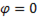Коэффициент мощности

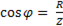= 1, (6-49)

так как Z =R

Таким образом, электрическая цепь переменного тока в режиме резонанса представляет собой чисто активную нагрузку.

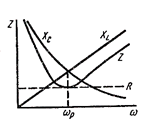
Зависимость параметров цепи от частоты. Практический интерес представляют соотношения между параметрами цепи и их зависимость от частоты тока. На рис.78 а показаны

а б

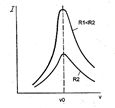
Рис.78

кривые 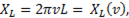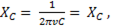R = R(v). Т.к. активное сопротивление практически от частоты не зависит то график R = R(v) представляет прямую параллельную оси абсцисс. Индуктивное сопротивление 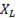прямо пропорционально, а емкостное сопротивление 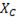обратно пропорционально частоте тока.

До резонанса 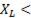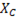, при резонансе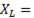 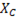, после резонанса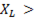 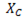. При резонансе полное реактивное сопротивление

=

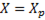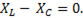
Полное сопротивление цепи Z, также зависит от частоты. До и после резонанса оно растет за счет увеличения 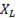или 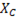. При резонансе Z = R.

По закону Ома ток в последовательной R, L, C – цепи

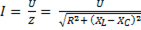. (6-50)

При резонансе (X_L =X_C) и ток равен максимальному значению, в то время как до (X_L < X_C) и после (X_L > X_C) резонанса он уменьшается. При v=0, X_C = ∞, I = 0. Аналогично при v =∞, X_L =∞, I = 0. На рис. б показаны графики I (v).

Кривая зависимости тока от частоты называется резонансной кривой. По характеру изменения тока в R, L, C – цепи легко установить состояние резонанса в ней – максимальное значение тока в цепи указывает на момент резонанса.

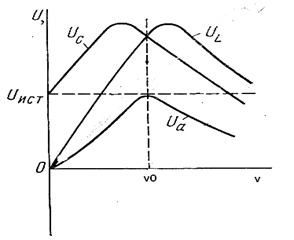
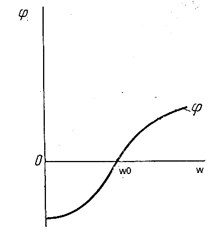
Рис. 79 Рис.80

Напряжение на резистивном элементе изменяется пропорционально току: 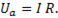При резонансе, когда ток максимален, напряжение U_a также максимально и равно напряжению источника питания U_ист (рис.). При ω = 0; ∞ ток I = 0; U_a = 0. На рис.79а изображена зависимость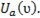

Напряжение на индуктивном элементе 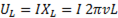пропорционально току I и частоте . .

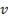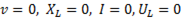При увеличении частоты напряжение на индуктивном элементе растет и при частоте, близкой к резонансной, достигает максимального значения; по мере дальнейшего увеличения частоты ток, а следовательно, и индуктивное напряжение уменьшаются. При 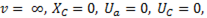поэтому индуктивное напряжение равно напряжению источника питания. Кривая 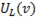изображена на рис. 79а.

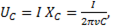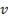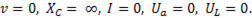Напряжение на емкостном элементе следовательно, оно пропорционально току I и обратно пропорционально частоте . При Поэтому емкостное напряжение компенсирует приложенное напряжение к цепи, т.е. 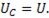При увеличении частоты напряжение 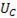растет и при частоте, близкой к резонансной, достигает максимального значения; по мере дальнейшего увеличения частоты ток и емкостное напряжение уменьшаются. При 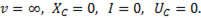Кривая 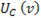изображена на рис..

Сдвиг фаз определяется из выражения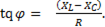

При 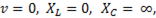т.е. 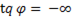, что соответствует .

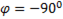При 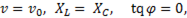что соответствует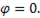

При 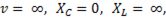т.е. 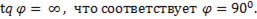График зависимости 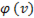изображен на рис. 80.

7. ПАРАЛЛЕЛЬНОЕ СОЕДИНЕНИЕ R, L, C – ЭЛЕМЕНТОВ

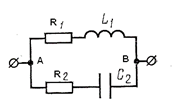
В цепь переменного тока параллельно включены реальная катушка индуктивности и конденсатор с потерями (рис. 81). Эту цепь можно представить как цепь с двумя ветвями, в одной из которых включены элементы R₁ и L₁, а в другой элементы R₂ и C₂ (рис. 81а). Ветви электрической цепи находятся под одинаковым напряжением

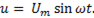(6-51)

а б в

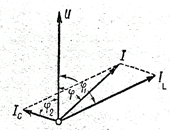
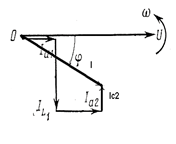
Рис. 81 Параллельное соединение R, L, C – элементов: а –схема, б.в – векторные диаграммы токов.

Первая ветвь содержит активное сопротивление и индуктивность, следовательно, ток отстает от напряжения на угол 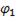, т.е

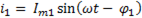. (6-52)

Причем,

,

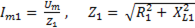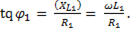
Характер второй ветви активно – емкостной, следовательно, ток опережает напряжение на угол 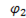и

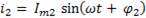. (6-53)

Причем,

,

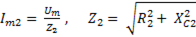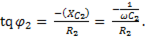
Полный или результирующий ток

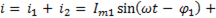
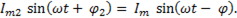(6-54)

При сложении получается синусоидальная величина с той же частотой и начальной фазой φ. Для нахождения 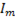и воспользуемся правилом векторного сложения .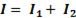

Построение векторной диаграммы начинаем с ориентации на плоскости вектора U ( рис. 81б,в). Под углом φ₁ к напряжению откладывается вектор амплитудного (с учетом знака), либо действующего значения тока I₁ в первой ветви, а под углом φ₂ вектор тока I₂ во второй ветви (с учетом знака). Суммируем вектора 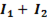(правило параллелограмма) и получаем вектор результирующего тока 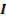. Модуль этого вектора определяем по теореме косинусов

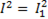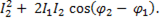+ (6-55)

Можно поступить иначе и от косого треугольника токов перейти к прямоугольному треугольнику.

Спроектируем вектора токов на вектор напряжения, получим активную составляющую тока:

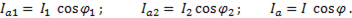(6-56)

Cоставляющие, направленные по линии, перпендикулярной линии напряжения, называют реактивными:

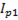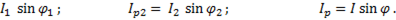= (6-57)

Составляющие результирующего тока могут быть определены как

Т.е. равны сумме составляющих отдельных ветвей. При этом необходимо учитывать их знак. Для ветви с индуктивным элементом реактивную составляющую тока берут со знаком плюс, для ветви с емкостным элементом – со знаком минус.

Из треугольника токов находим

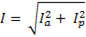. (6-58)

Электрическая проводимость. Каждый элемент цепи может характеризоваться сопротивлением или проводимостью. Разделим все стороны треугольников токов (рис. 81в) на напряжение. Получим треугольник проводимостей, где каждая из сторон представляет соответствующую проводимость.

Отношение активного тока к напряжению – активная проводимость q:

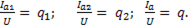(6-59)

Отношение реактивного тока к напряжению – реактивная проводимость b:

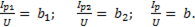(6-60)

Отношение результирующего тока к напряжению – полная проводимость y:

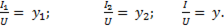(6-61)

Единица измерения проводимости –сименс (См=1/ом).

Из диаграммы видно, что составляющие полной проводимости могут быть определены как

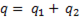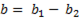; ; (6-62)

Тогда полная проводимость

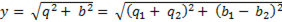. (6-63)

Аналогично для каждой отдельной ветви можно записать

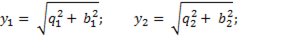
Воспользовавшись диаграммой можно записать

= = =

= = =

= = =

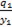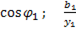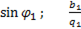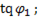
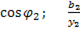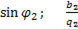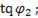
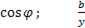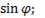
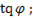
Связь между сопротивлением и проводимостью. Часто при решении практических задач исходными данными являются сопротивления отдельных элементов цепи, а необходимо определить проводимости и сопротивления всей цепи.

Известно, что 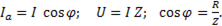Если эти значения подставить в (), то

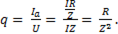(6-64)

Аналогично 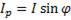; 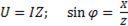. Подставляя эти выражения в (), получим

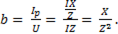(6-65)

Реактивные проводимости сохраняют знак соответствующего сопротивления, т.е.

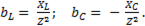(6-66)

Полную проводимость можно получить из ()

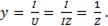(6-67)

Таким образом, полная проводимость цепи равна обратной величине полного сопротивления.

Электрическая мощность. Диаграмму мощностей можно получить из диаграммы токов. Для этого необходимо модули токов умножить на напряжение U:

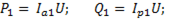(6-68)

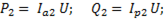
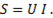(6-69)

Из диаграммы мощностей следует

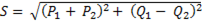. (6-70)

Таким образом, при любом числе элементов, включенных параллельно, результирующие ток, проводимость, мощность записываются как корень квадратный из суммы квадратов арифметических сумм активных и алгебраических сумм реактивных значений соответствующих параметров.

Дата добавления: 2015-05-06