Электрическая цепь с емкостным элементом

На рис. 72 в цепь переменного тока включен идеальный элемент, обладающий только емкостью С. Активным и индуктивным сопротивлениями этого элемента пренебрегаем, т.е. R_c = L = 0.

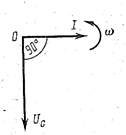
а б в

Рис. 72 Цепь переменного тока с емкостным элементом: а- схема, б,в – временная и векторная диаграммы.

При подключении пременного напряжения u = U_m 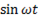вследствие периодической перезарядки конденсатора в цепи проходит ток, который можно определить как скорость изменения заряда на обкладках конденсатора.

Уравнение тока.

i =dq/dt, (6-18)

т.к емкость конденсатора C=q/u_c, то dq = C du_c.

Тогда i =dq/dt = C∙du_c/dt. В цепи для любого момента времени выполняется соотношение u=uc = U_m 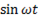. С учетом этого

i =C d(U_m 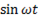)/dt. (6-19)

Продифференцировав это выражение, получим

i =CU_mω .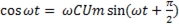

Обозначим 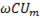= I_m

и выражение для тока примет вид:

i = I_m 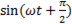. (6-20)

Таким образом, в цепи с емкостным элементом кривая тока опережает кривую напряжения по фазе на угол π/2. Это означает, что с нарастанием напряжения от нуля до максимума ток падает от максимума до нуля (рис.72 б).

Действующее значение тока определим из соотношения:

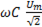
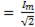
или

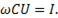(6-21)

Напряжение и ток в рассматриваемой цепи можно изобразить с помощью векторной диаграммы (рис. в). Если вектор тока расположить горизонтально (удобно для сравнения с предыдущими векторными диаграммами), то вектор напряжения, отстающий по фазе на угол откладывается вниз.

Емкостное сопротивление. Изуравнения (6-21) следует

U/I = 1/ωC, (6-22)

где 1/ωC = Xc – емкостное сопротивление.

Следовательно,

Xc = 1/ωC = 1/2πνC. (6-23)

Емкостное сопротивление обратно пропорционально частоте и емкости элемента, т.е. с увеличением частоты от нуля до бесконечности величина Xc уменьшается от бесконечности до нуля.

Измеряется это сопротивление в омах (ом)

Емкостное сопротивление – это сопротивление току, которое оказывает электрическое поле, возникающее вокруг накапливаемого на пластинах конденсатора заряда.

Закон Ома в комплексном виде. Комплекс напряжения Ù = U 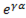. Комплекс тока Í = I 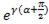. Комплекс сопротивления Ż = Ù/Í = U/I ∙ = Xc = ( - ) = - .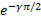

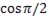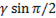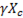Ù = - 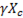Í. (6-24)

Комплекс сопротивления электрической цепи с конденсатором является отрицательным мнимым числом, модуль которого равен .

Уравнение мощности. Если в цепь переменного тока включен только конденсатор, то уравнения для мгновенных значение напряжения и тока запишутся как

u = U_m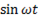

и

i = I_m .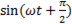

Рис. 73

Тогда

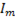
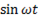
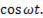
Подставляя в это выражение 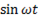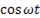= 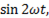получим

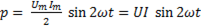. (6-25)

Мощность в рассматриваемой цепи изменяется аналогично мощности в цепи с индуктивным элементом, т.е. синусоидально с удвоенной частотой 2ω. Как следует из рис. 73, мощность положительна (вторая и четвертая четверти периода), когда ток и напряжение имеют одинаковые знаки, и отрицательна (первая и третья четверти периода, когда ток и напряжение имеют различные знаки. Кроме того, во время увеличения абсолютного значения напряжения мощность цепи положительна, а во время его уменьшения – отрицательна. Это объясняется тем, что с увеличением напряжения конденсатор заряжается, между его пластинами создается электрическое поле и увеличивается энергия, запасенная этим полем (ток уменьшается). 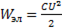. Когда конденсатор разряжается, энергия поля уменьшается, переходит в электрическую и возвращается к источнику питания (ток возрастает).

Мощность, как скорость преобразования энергии отображает процесс преобразования электрической энергии источника и энергии электрического поля конденсатора.

Таким образом, в цепи с емкостным элементом происходит периодический обмен энергии без преобразования электрической энергии источника в тепловую или механическую.

Активная мощность рассматриваемой цепи:

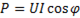=0.

Так как в цепи с конденсатором ток опережает напряжение на 90⁰, то φ = 90⁰; 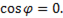Поэтому активная мощность также равна нулю, т.е. в такой цепи, как и в цепи с чистой индуктивностью, расхода мощности нет.

Для установления скорости обмена энергии в рассматриваемой цепи аналогично цепи с индуктивным элементом вводится понятие реактивной (емкостной) мощности:

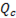= UI (6-26)

Реактивная мощность измеряется в варах.

5. ПОСЛЕДОВАТЕЛЬНОЕ СОЕДИНЕНИЕ R, L, C – ЭЛЕМЕНТОВ.

На рис.74 в цепь переменного тока последовательно включены резистор, идеальная катушка индуктивности и идеальный конденсатор. Эту цепь можно представить как последовательное соединение активного сопротивления R, индуктивного сопротивления X_L и емкостного сопротивления X_c.

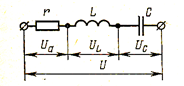
Рис.74

Уравнение напряжений. При протекании в цепи синусоидального тока

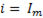
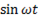(6-27)

на каждом элементе цепи создается падение напряжения: на резисторе – активное падение напряжения U_a = U_R; на катушке – индуктивное падение напряжения U_L; на конденсаторе - емкостное падение напряжения U_c.

Мгновенное значение полного (общего или результирующего) значения напряжения в любой момент времени

u = u_a + u_L + u_c. (6-28)

Причем активная составляющая напряжения

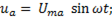(6-29)

индуктивная

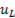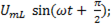= (6-30)

емкостная

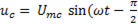). (6-31)

Результирующее напряжение

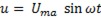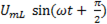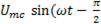+ + ). (6-31)

Для нахождения амплитудного или действующего значения результирующего напряжения и фазового сдвига между напряжением и током воспользуемся векторной диаграммой действующих значений напряжений. Построение осуществляется в такой последовательности:

1) вектор тока I откладывается по горизонтальной прямой, так как его начальная фаза равна нулю;

2) вектор U_a совпадает по фазе с вектором I;

3) от конца вектора U_a откладывается вектор U_L, направленный вертикально вверх (начальная фаза +π/2);

4) от конца вектора U_L откладывается вектор U_c, направленный вертикально вниз (начальная фаза –π/2);

5) складывая векторы U_a, U _L, U_c, получаем вектор результирующего напряжения цепи

U = U_a + U_L + U_c. (6-32)

Модуль результирующего напряжения находится из прямоугольного треугольника:

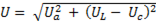. (6-33)

Нахождение результирующего напряжения с использованием векторного сложения напряжений на отдельных участках цепи возможно с использованием правила параллелограмма.

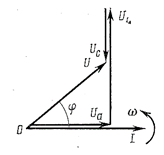
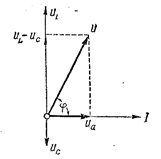
а б

Рис. 75 Диаграммы напряжений для R, L, C – цепи.

Напряжения 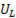и сдвинуты по фазе на 180⁰ (находятся в противофазе). Поэтому при геометрическом сложении векторов они взаимно вычитаются. Векторная разность 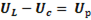называется реактивным напряжением. Складывая вектора 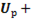U_a по правилу параллелограмма, находим величину и направление вектора результирующего напряжения U.

Анализируя векторную диаграмму напряжений для RLC-цепи, можно сделать вывод, что при U_L > U_c вектор результирующего напряжения опережает вектор тока на угол φ < 90⁰, а при U_L < U_c результирующий вектор напряжения отстает от вектора тока на угол φ < 90⁰.

Из треугольника напряжений тригонометрические функции угла сдвига фаз можно записать в виде:

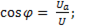
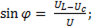
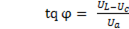; (6-34)

Треугольник сопротивлений. Поделив каждую сторону треугольника напряжений на одно и то же число (на ток) получим подобный треугольник – треугольник сопротивлений для RLC-цепи, т.е. 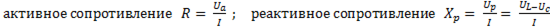; полное сопротивление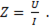

Величина полного напряжения определяется выражением 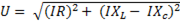, а ток в цепи равен

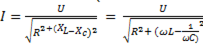. (6-35)

Тогда полное сопротивление последовательной RLC-цепи равно:

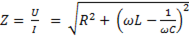. (6-36)

Из треугольника сопротивлений следует, что фазовый сдвиг между током и полным напряжением определяется из условия:

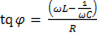. (6-37)

Видно, чем больше активное сопротивление, тем меньше сдвиг фаз.

Уравнение мощности. Треугольник мощностей. Для построения треугольника мощностей умножим все стороны треугольника напряжений на ток . Тогда активная мощность

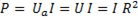. (6-38)

Измеряется активная мощность в ваттах (ВТ).

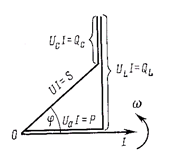
Рис.76

Индуктивная мощность

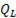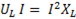= . (6-39)

Емкостная мощность

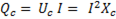. (6-40)

Полная реактивная мощность

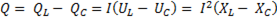. (6-41)

Измеряется реактивная мощность – вольт –ампер - реактивный (ВАР)

Полная мощность цепи

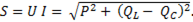(6-42)

Измеряется полная мощность - вольт на ампер (ВА).

Дата добавления: 2015-05-06