Трехфазные электрические цепи

1. ПРИНЦИПЫ ПОСТРОЕНИЯ ТРЕХФАЗНЫХ ЭЛЕКТРИЧЕСКИХ ЦЕПЕЙ

Трехфазная система является основной системой силовой электроэнергетики. В настоящее время получение, преобразование, передача и распределение электроэнергии в большинстве случаев производится посредством трехфазной системы. Благодаря хорошим техническим и экономическим характеристикам трехфазный ток обеспечивает наиболее простую передачу электрической энергии, позволяет создать относительно простые по устройству и экономичные генераторы, двигатели, трансформаторы и различную коммутационную аппаратуру.

Эта система была изобретена и практически разработана русским инженером М.О. Доливо-Добровольским в конце 19 века.

Основные достоинства трехфазной системы:

1) простота конструкции и эксплуатации трехфазных генераторов и двигателей,

2) большая экономия в массе проводов при передаче электроэнергии на большие расстояния (20-30% по сравнению с однофазной системой),

3) возможность получения различных напряжений (линейные и фазные) в одной и той же трехфазной системе.

Для выяснения принципа создания трехфазной системы представим себе трехфазный генератор как машину с тремя совершенно одинаковыми изолированными друг от друга катушками (обмотками) на статоре, в центре которого вращается электромагнит (рис. 84а).

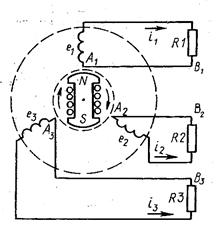
а б в

Рис. 84 Устройство трехфазного генератора: а – схема, временная (б) и векторная (в) диаграммы.

Пусть при этом форма магнита такова, что магнитный поток, пронизывающий каждую катушку, изменяется по косинусоидальному закону. Тогда по закону электромагнитной индукции в катушках будут индуцироваться синусоидальные эдс равной амплитуды и частоты, но отличные друг от друга по фазе на угол 120⁰:

= (6-82)

Эти три эдс можно изобразить на временной (рис. 84 б) и на векторной (рис. 84 в) диаграммах.

Простоты ради будем считать, что все три линии генератора нагружены одинаковыми активными сопротивлениями R₁ = R₂ = R₃. Тогда токи будут совпадать по фазе с соответствующими эдс:

= (6-83)

Будем считать, что токи, идущие от генератора к приемнику в проводах, от трех, например, концов (или трех начал) обмоток генератора будут положительными. Тогда очевидно, что такая система электрических цепей позволяет уменьшить число соединительных проводов.

а б

Рис. 85 Образование соединения фаз звездой: а – схема электрически несвязанной трехфазной системы, б – объединенная трехфазная система.

Действительно, соединив, например, три обратных провода А₁В₁, А₂В₂, А₃В₃ в один, получим четыре провода (рис.85 б) вместо шести (рис.85 а). В результате такого соединения получим провод ОО' вместо трех, в котором, очевидно, установится ток, равный векторной сумме трех токов, т.е.

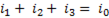(6-84)

или

I₁ + I₂ + I₃ = I₀. (6-85)

1. СОЕДИНЕНИЕ ЗВЕЗДОЙ. ЧЕТЫРЕХПРОВОДНАЯ СИСТЕМА.

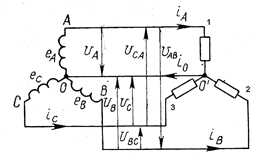
Рассмотрим схему соединения обмоток генератора звездой, в которой концы трех обмоток (x, y, z) соединяются в один узел, а начала (A, B, C) служат зажимами для подключения нагрузки (рис.86а).

При таком способе соединения напряжение между каждой фазой и нулевым (нейтральным, уравнительным) проводом ОО' называют фазным напряжением. Оно обозначается U_ф или U_А; в последнем случае индекс указывает, что взято напряжение между нулевым проводом и фазой А.

а б

Рис.86

Напряжения между линейными (А, В, С) проводами называют линейными. Они обозначаются U_л или U_АВ, U_ВС, U_СА (U₁₂, U₂₃,U₃₁).

Линейные напряжения представляют собой разность потенциалов между точками А и В, В и С, С и А. Выберем условно точку (точки), у которых потенциал равен нулю. В трехфазных цепях потенциал нулевого провода принимается равным нулю, а нулевой провод, как правило, соединяют с землей (заземляют). Тогда потенциалы точек А, В, С будут соответственно равны φ_А, φ_В, φ_С, а линейные напряжения представляют собой разности потенциалов этих точек, т.е.

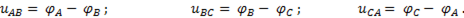(6-86)

Фазные напряжения

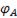= - (6-87)

Перепишем последние выражения и представим в виде:

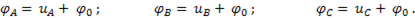(6-88)

Подставим выражения для 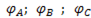в уравнения (6-86) получим

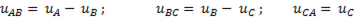- (6-89)

В векторной форме последние выражения имеют вид:

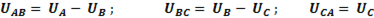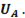- (6-90)

Сложим векторы

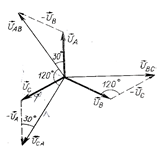
- и построим векторную диаграмму (рис.86б).

В результате построений получили три вектора, которые образуют симметричную трехлучевую звезду линейных напряжений, повернутую относительно звезды фазных напряжений на угол 30⁰ против часовой стрелки.

Для установления соотношения между абсолютными значениями линейного и фазного напряжений рассмотрим тупоугольный треугольник с углом 120⁰ при вершине, образованный, например, векторами 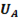, 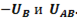Из этого треугольника следует:

(6-91)

В случае симметричной нагрузки

, то

= (6-92)

откуда

(6-93)

Если линейное напряжение 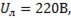то фазное равно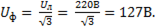

Если же напряжение 220В принять фазным, то линейное напряжение равно

=

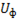
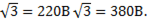
В случае соединения звездой с нейтралью (четырехпроводная линия) в этой системе существует два вида напряжений - линейное и фазное, что является достоинством четырехпроводной системы.

Система 380/220В является более экономичной, нежели система 220/127В, так как для электропередачи при одной и той же мощности требуется меньший расход металла на провода за счет меньшего тока.

Токи в фазах приемника и нулевом проводе. При соединении приемника звездой в точках перехода из линии в фазы отсутствуют какие – либо разветвления, поэтому фазные и линейные токи одинаковы:

(6-94)

Для каждой фазы трехфазной цепи применимы все формулы, полученные ранее для однофазных цепей, в том числе:

= = (6-95)

Для нахождения значений тока в нулевом проводе при симметричной нагрузке, найдем его мгновенное значение, сложив значения токов

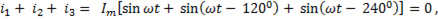(6-96)

т.е. суммарный ток в нулевом проводе при симметричной нагрузке равен нулю.

Это же суммирование можно произвести и с помощью векторов так, как это показано на рис. 87а, т.е.

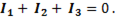(6-97)

а б

Рис.87

Очевидно, что при I ₀ =0 необходимость в нулевом проводе отсутствует и тогда четырехпроводная система преобразуется в трехпроводную (рис.87б).

Трехпроводная система (соединение «звезда») используется в случаях, когда нагрузка в фазах приемника симметричная. Например, при подключении трехфазных двигателей, обмоток трехфазных трансформаторов, трехфазных нагревательных печей и т.д.

1. СОЕДИНЕНИЕ ЗВЕЗДА. НЕСИММЕТРИЧНАЯ НАГРУЗКА. ЯВЛЕНИЕ ПЕРЕКОСА ФАЗ

В данном параграфе будут рассмотрены следующие случаи несимметрии трехфазной системы при условии, что генератор возбуждает симметричные фазные эдс

а) несимметричная нагрузка в фазах приемника;

б) обрыв одного из питающих проводов линии;

в) короткое замыкание одной из фаз приемника.

Несимметричная нагрузка в фазах приемника. На рис. представлено соединение генератор – приемник по схеме звезда – звезда с нейтральным проводом, причем 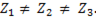Сопротивлением подводящих проводов ввиду малости пренебрегаем, 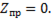Тогда потенциал точки А равен потенциалу точки 1, точки В – потенциалу 2, точки С – потенциалу 3. Нейтральный провод имеет отличное от нуля сопротивление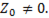

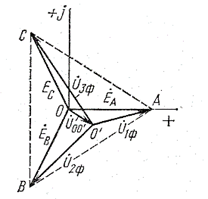
а б

Рис.88

Несимметричная трехфазная цепь, показанная на рис.88а, может рассматриваться как трехконтурная цепь с тремя эдс и двумя узлами. Такая цепь может быть рассчитана методом узлового напряжения (см. приложение).

Определим узловое напряжение, т.е. падение напряжения на нулевом проводе:

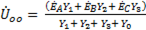. (6-98)

Фазное напряжение приемника равны разности между комплексом эдс генератора и комплексом узлового напряжения (напряжения между нейтральными точками генератора и приемника):

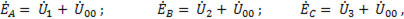(6-99)

откуда напряжения в фазах приемника

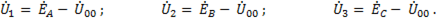(6-100)

Токи в фазах приемника

; (6-101)

Ток в нейтральном проводе

(6-102)

На рис.88б дана векторная диаграмма фазных эдс генератора и напряжений фаз приемника при несимметричной нагрузке.

Диаграмма эдс генератора представляет собой трехлучевую симметричную звезду, где модули векторов одинаковы и сдвинуты по фазе на угол 120⁰. Начало координат есть узловая точка О генератора. Из точки О откладывается вектор 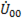, направление и величина которого определяется комплексом, вычисленным по формуле (). Конец вектора 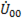есть узловая точка приемника О'. Напряжения фаз приемника в соответствии с уравнениями определяются векторами, соединяющими узловую точку О' с точками А, В и С.

Из диаграммы рис. следует, что фазные напряжения приемника различны между собой и по величине и по сдвигу фаз. Узловая точка О симметрична относительно векторов эдс генератора, в то время как узловая точка приемника О' смещена в сторону. Это явление называется перекосом фаз напряжений приемника. Перекос фаз в трехфазных системах – нежелательное явление, так как нарушает нормальную работу приемников электроэнергии.

Обрыв линейного провода. Допустим, что в симметричной трехпроводной системе с равномерной нагрузкой при соединении генератора и приемника по схеме звезда – звезда произошел обрыв одного из линейных проводов, например перегорел предохранитель в проводе А (рис.89 а).

В этом случае

=

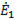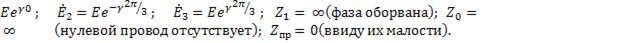
а б

Рис.89

Напряжение между узловыми точками

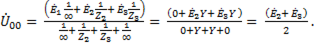(6-103)

Известно, что для генератора откуда

(6-104)

Следовательно,

(6-105)

т.е. узловое напряжение численно равно половине фазной эдс генератора, взятой с обратным знаком.

На рис. 89б дана векторная диаграмма эдс генератора, напряжений приемника, узлового напряжения и напряжения на контактах перегоревшего предохранителя.

Напряжение первой фазы приемника равно нулю, так как при обрыве провода следовательно, =0.

Напряжение на контактах перегоревшего предохранителя определяется как разность эдс генератора и узлового напряжения:

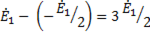= , (6-106)

т.е. напряжение на контактах перегоревшего предохранителя достигает полуторной величины эдс фазы генератора. Это необходимо помнить эксплуатационникам, занимающимися поиском поврежденных мест в трехфазной системе.

Напряжение второй фазы приемника равно разности между эдс второй фазы и узловым напряжением:

(6-107)

т.е. напряжение на второй фазе приемника равно половине линейного напряжения генератора.

Напряжение третьей фазы приемника

(6-108)

т.е. напряжение третьей фазы приемника численно равно напряжению второй фазы, взятому с обратным знаком.

Диаграмма токов строится в соответствии с характером нагрузки. При этом угол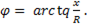

По закону Ома

(6-109)

Ток в оборванной фазе равен нулю.

Короткое замыкание одной из фаз приемника. Допустим, что в симметричной трехфазной системе с равномерной нагрузкой при соединении генератора и приемника по схеме звезда – звезда без нулевого провода произошло замыкание одной из фаз приемника, например фазы А (рис.90а).

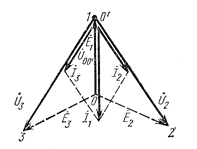
а б

Рис.90

В этом случае

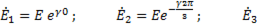= =0(фаза замкнута накоротко); .

При этом потенциалы точек 1 и 0' равны между собой (короткое замыкание фазы), потенциалы точек А и 1 также равны, поскольку сопротивления проводов не учитывается. Таким образом, потенциалы точек А и 0' равны между собой. Следовательно, эдс фазы генератора равна узловому напряжению, т.е. 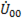= 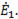То же самое можно получить, если воспользоваться формулой

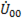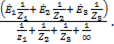= (6-110)

Разделим каждый член числителя и знаменателя на или (что то же самое) умножим и разделим на после чего приравняем сопротивление 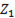нулю.

Тогда

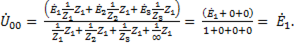(6-111)

На рис. 90 б показана векторная диаграмма эдс и напряжений при коротком замыкании одной из фаз приемника. Из диаграммы видно, что 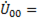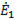и точка 0' оказывается совмещенной с точкой 1, т.е. их потенциалы равны между собой.

Для определения напряжения в фазах приемника воспользуемся аналогичными выражениями, составленными по второму закону Кирхгофа для отдельных контуров:

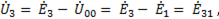(6-112)

т.е. на каждой из двух оставшихся фаз приемника напряжение равно линейной эдс генератора.

Комплексы токов соответственно

(6-113)

На диаграмме показаны токи для случая активной нагрузки. Ток в питающем проводе, фаза которого замкнута, определится как геометрическая сумма токов в остальных фазах. При замыкании первой фазы ток в питающем проводе

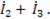
1. НУЛЕВОЙ ПРОВОД

Рассмотренные случаи несимметрии в трехфазных цепях, так или иначе приводят к изменению напряжений приемника и сдвига фаз между ними. Изменение напряжений влечет за собой изменение токов, т.е. перекос фаз. Перекос фаз в трехфазной цепи создает неодинаковые напряжения на фазах приемника, несмотря на симметрию фазных эдс источника питания. Это недопустимо, так как создается аварийный режим работы трехфазной системы.

Напряжение на нейтральном проводе по закону Ома

. (6-114)

Из выражения следует, что напряжение на нулевом проводе равно нулю при 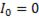или = 0.

Как известно, ток в нулевом проводе 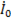= 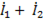+ 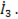При симметричной нагрузке

В остальных случаях ток в нулевом проводе имеет отличную от нуля величину и будет тем больше, чем сильнее отличаются нагрузки в фазах приемника.

Теоретически сопротивление нулевого провода никогда не может быть равным нулю, так как любой провод, соединяющий точи 0 и 0', всегда обладает каким-то сопротивлением. Однако практически, если сечение нулевого провода составляет 0,3 – 0,5 от сечения линейного провода и имеет хорошие контакты, то считается, что = 0. Тогда .

Таким образом, напряжение на фазах приемника будет равно эдс фаз генератора и система приемника будет симметричной, хотя нагрузки на фазах приемника неодинаковы.

Нулевым является провод, выравнивающий потенциалы точек 0 и 0', поэтому его часто называют уравнительным. Отсутствие нулевого провода 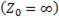при несимметричной нагрузке приводит к перекосу системы. Следовательно, функция нулевого провода состоит в том, чтобы при несимметричной нагрузке фаз приемника сохранить симметричность системы приемника. Кроме того, наличие нулевого провода дает возможность получить от генератора не только линейное, но и фазное напряжение, что очень важно при электроснабжении.

1. ТРЕХПРОВОДНАЯ СИСТЕМА. СОЕДИНЕНИЕ ТРЕУГОЛЬНИКОМ.

Обмотки трехфазного генератора, а также трехфазные нагрузки могут быть соединены еще одним способом: конец первой обмотки соединяют с началом второй, конец второй – с началом третьей, конец третьей – с началом первой, а узлы соединения служат отводами (рис. 91 а). Такой способ соединения называют треугольником.

а б

Рис.91

Кажущегося короткого замыкания в обмотках генератора не произойдет, так как в любой момент времени сумма эдс в его обмотках равна нулю:

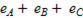=0 (6-115)

и ток при отсутствии внешней нагрузки в замкнутом треугольнике также равен нулю.

Это справедливо в том случае, если все три эдс строго синусоидальны. Но в работе генератора форма эдс может отклоняться от синусоидальной, поэтому соединение треугольником обмоток генератора, как правило, не применяют. Однако соединение треугольником широко используется у трехфазных потребителей, создающих симметричную нагрузку (двигатели, печи, осветительные системы и т.д.).

Если включить фазы приемника тока: 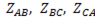(рис.91 а)- непосредственно между линейными проводами трехпроводной системы, то получим соединение токоприемников треугольником. При таком соединении нет различия между фазным и линейным напряжениями, так как напряжение между началом и концом каждой фазы приемника является в то же время линейным напряжением, т.е.

(6-116)

В общем виде

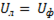. (6-117)

Если различие между фазным и линейным напряжениями в соединении треугольником отсутствует, зато появляется различие между фазными (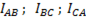) и линейными ( токами приемника.

Построим векторные диаграммы токов и найдем зависимость между их абсолютными значениями. Условимся положительными направлениями фазных токов считать направления от А к В, от В к С и от С к А, а положительными направлениями линейных токов – направления от генератора к приемнику. Тогда по первому закону Кирхгофа имеем:

(6-118)

откуда

Из последних соотношений видно, что любой из линейных токов равен геометрической разности фазных токов.

Также следует, что при любых равных значениях фазных токов геометрическая сумма линейных токов равна нулю, т.е.

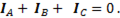(6-119)

В случае симметричной нагрузки ( = векторы фазных токов одинаково сдвинуты по фазе на угол φ относительно соответствующих векторов напряжений и создают симметричную трехлучевую звезду фазных токов (рис.91б).

Для построения на этой же диаграмме векторов линейных токов воспользуемся соотношениями (), на основании которых вектор каждого линейного тока представляет собой разность между двумя соседними векторами, отсчитанными против часовой стрелки. Произведя построения, аналогичные построениям векторов линейных напряжений (см. рис.), получим, что векторы линейных токов образуют трехлучевую звезду, повернутую относительно звезды фазных токов на 30⁰. Из полученной диаграммы видно, что линейные токи представляют собой основания равнобедренных треугольников с углами 120⁰ при вершине. Из диаграммы следует, что соотношение между фазными и линейными токами равно

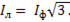(6-120)

Таким образом, два способа включения потребителей (звездой или треугольником) расширяет возможности использования этих потребителей. Например, если каждая из трех обмоток трехфазного электродвигателя рассчитана на рабочее напряжение 220В, то, электродвигатель может быть включен треугольником в сеть 220/127B или звездой в сеть 380/220В.

1. МОЩНОСТЬ ТРЕХФАЗНОЙ СИСТЕМЫ

Активная мощность трехфазной системы равна арифметической сумме активных мощностей всех фаз:

(6-121)

т.е.

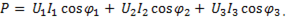(6-122)

При симметричной нагрузке

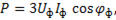(6-123)

где 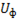и - фазные напряжение и ток; - сдвиг фаз между током и напряжением.

На практике иногда удобнее измерять мощность не через фазные, а через линейные напряжения и токи. Так, для соединения звездой имеем:

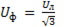и 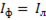, (6-124)

а при соединении треугольником –

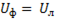и , (6-125)

так что в обоих случаях произведение дает

= ,

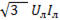тогда мощность трехфазной системы при симметричной нагрузке может быть выражена через линейные величины:

(6-126)

где φ – угол сдвига между линейным током и напряжением.

Для трехфазной системы остаются справедливыми соотношения:

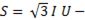полная мощность, 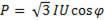-активная мощность, реактивная мощность, а также

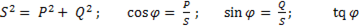= (6-127)

Контрольные вопросы

1. Какие достоинства имеет трехфазная система?

2. Чему равен фазовый сдвиг между эдс в трехфазной системе?

3. Сколько нужно проводов для соединения генератора с приемником в несвязанной трехфазной системе?

4. Каково соотношение между линейными и фазными токами и напряжениями при соединении звездой?

5. Каково соотношение между линейными и фазными токами и напряжениями при соединении треугольником?

6. Обосновать основное преимущество четырехпроводной системы по сравнению с трехпроводной для соединения звезда.

7. Какими последствиями сопровождается неправильное соединение звездой (треугольником) обмоток генератора?

8. Чему равен ток в нейтральном проводе при симметричной нагрузке приемника и соединении фаз звездой?

9. Каким образом можно определить, который из проводов четырехпроводной трехфазной линии является нулевым?

10. В чем особенность явления перекоса фаз?

11. Три одинаковых резистора включены звездой в трехпроводную цепь. Как изменятся токи при обрыве одного провода?

1. В каких случаях применят на практике трехпроводную систему для приемников энергии, соединенных звездой?
2. Как изменятся токи в трехпроводной системе при коротком замыкании одной из фаз?
3. Объяснить, почему в нейтральном проводе четырехпроводной системы не устанавливают предохранитель и сечение его меньше сечения линейных проводов.
4. Пояснить, почему трехфазный двигатель можно включать в трехфазную сеть без нейтрального провода?

16. Во сколько раз возрастут линейные токи, если приемник энергии пересоединить со схемы звезды на схему треугольник?

Г л а в а 8

Дата добавления: 2015-05-06