Пример 1.13

Использование графа электрической цепи

При анализе сложных электрических цепей следует использовать направленный граф цепи. В этом случае система узловых уравнений в матричной форме принимает следующий вид.

, (1.10)

где А – матрица соединений, правила составления которой с помощью направленного графа цепи рассматривались ранее; Ф – матрица столбец неизвестных потенциалов; Y – диагональная матрица проводимостей ветвей; Е – матрица столбец ЭДС ветвей, J – матрица столбец источников тока ветвей.

Рассмотрим пример использования матричного уравнения (1.10).

На рис. 1.29 приведена электрическая цепь, в которой надо найти неизвестные токи методом узловых потенциалов. На рис. 1.30 приведён направленный граф данной цепи.

Оформим листинг решения задачи. Зададимся исходными данными.

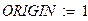
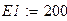
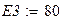
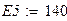
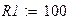
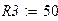
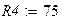
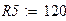
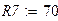
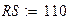
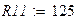
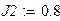
Составим столбцовые матрицы ЭДС ветвей, источников тока ветвей и диагональную матрицу проводимостей ветвей. Для этого вначале составим столбцовую матрицу сопротивлений ветвей. Для определения знаков используем понятие условно-положительных направлений в обобщённой ветви, которое рассматривалось выше.

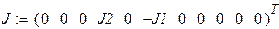
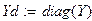
Рисунок 1.29

Рисунок 1.30

Составим матрицу соединений по правилам, которые рассматривались выше (см. Пример 1.7). Найдём левую и правую части матричного уравнения (1.8), а затем и неизвестные потенциалы.

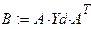
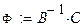
Составим матрицу напряжений на ветвях. Учитывая большую длину, разделим её на две матрицы, а затем составим одну матрицу с помощью оператора слияния строковых матриц.

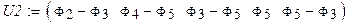
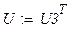
Найдём неизвестные токи, решая систему уравнений в матричной форме, составленную по второму закону Кирхгофа для ветвей схемы.

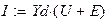
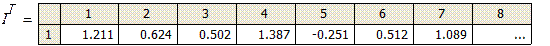
Используя прокрутку, можно увидеть в таблице значения всех найденных токов. Пятый, девятый и одиннадцатый токи отрицательные, следовательно, реальные направления данных токов противоположны направлениям соответствующих ветвей графа, которые были выбраны произвольно. Реальные направления токов наносятся на исследуемую электрическую цепь (рис. 1.29).

В заключение проверим баланс мощностей источников электрической энергии и приёмников.

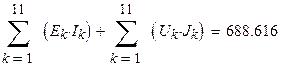
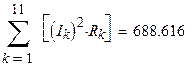
Баланс мощностей выполняется.

Построим потенциальную диаграмму для контура, образованного ветвями графа 2-1-6-9-10.

При построении потенциальной диаграммы учтём промежуточные точки между источниками ЭДС и резисторами.

Составим матрицы координат.

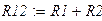
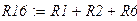
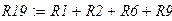
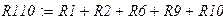
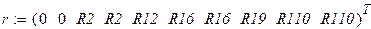
Построим потенциальную диаграмму. Узловые точки на графике обозначим после его импортирования.

Рисунок 1.31

1.5. Численное исследование электрической цепи

методом эквивалентного генератора

Численные методы анализа электрических цепей позволяют выполнить исследования состояний цепи любой сложности. Для исследования режимов в одной ветви используют метод эквивалентного генератора. В этом случае пассивная часть исследуемой ветви рассматривается как нагрузка активного двухполюсника, который включает в себя всю остальную электрическую цепь. Объём вычислений уменьшается, так как нет необходимости рассчитывать все неизвестные токи.

Рассмотрим пример использования метода эквивалентного генератора для определения зависимости выделяемой мощности в резисторе заданной ветви сложной электрической цепи от сопротивления этого резистора.

Дата добавления: 2015-05-06