Докажите формулу замены переменной для неопределенного интеграла

Пусть функция x=g(t) определена и дифференцируема на промежутке Т и Х-множество ее значений, на котором определена f(x). Тогда если F(x)-первообразная для f(x) на Х, то F(g(t))-первообразная для f(g(t))g’(t) на Т, т.е. на множестве Т выполняется равенство

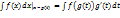(1)

Доказательство. По правилу дифференцирования сложной функции

F_t’(g(t))=F’_x(g(t))*g’(t)=f(g(t))*g’(t)

Что совпадает с подынтегральной функцией в правой части равенства,и это доказывает равенство(1)

5. Докажите, что если функция f (x) непрерывна на отрезке [a;b], то функцияF(x)= 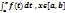является ее первообразной на этом отрезке

Если функция f(t) непрерывна на отрезке [a,b], то функция F(x)= 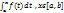дифференцируема на (a,b) и F’(x)=f(x) Доказательство

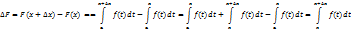
По теореме о среднем найдется точка с 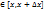такая,что 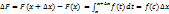. Так как f(x) непрерывна и с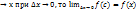

Поэтому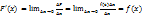

6. Используя свойство интеграла с переменным верхним пределом, докажите формулу Ньютона-Лейбница.

Пусть F(x) является первообразной для непрерывной на отрезке [a,b] функции f(x). Тогда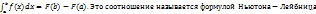

Т.к. функция f(x) непрерывна на [a,b], то она интегрируема на нем и имеет первообразную F(x)=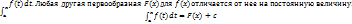

Подставляя х=а, получим 0=F(a)+c, т.е. с=-F(a). Тогда

7. Применив замену переменной в определенном интеграле, докажите, что для любой четной непрерывной на отрезке[-a; a] функции f (x) справедливо равенство 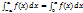. В чем состоит его геометрический смысл?

Так как f(x) непрерывна на [-a,a], тогда пусть х=g(t) определена на [ 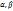] и имеет производную внутри этого отрезка, причем g(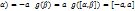

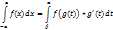
Доказательство

Пусть F(x) – первообразная f(x), тогда F’(x)=f(x) F(g(t))’=F’(g(t))*g’(t)

Можно заметить, что если подынтегральная функция f(x) четная на отрезке [a,b], то F(x) нечетна на этом отрезке, т.е. F(-x)=-F(x)

1)рассмотрим 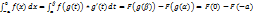=F(0)+F(a)

2) рассмотрим 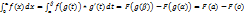=F(a)+F(0)

Получается, что они равны, ч.т. д

Геометрический смысл. Определенный интеграл равен площади криволинейной трапеции, ограниченной вертикальными прямыми х=а, x=b при a<b, осью Ох и графиком неотрицательной и непрерывной функции y=f(x)

1. Докажите, что если F₁(x) и F₂(x) первообразные функции f(x) на интервале Х, то F₂(x)= F₁(x)+c, где с-произвольная постоянная

Пусть F₁(x) и F₂(x) первообразные функции f(x) на интервале Х,тогда из определения первообразной F₁’(x)=f(x) и F₂’(x)=f(x)

(F₁(x)+c)’= F₁’(x)+c’=f(x)+0=f(x) F₂(x)= F₁(x)+c,ч.т.д

8. Применив замену переменной в определенном интеграле, докажите, что для любой четной непрерывной на отрезке[-a; a] функции f (x) справедливо равенство 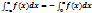. В чем состоит его геометрический смысл?

Так как f(x) непрерывна на [-a,a], тогда пусть х=g(t) определена на [ 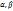] и имеет производную внутри этого отрезка, причем g(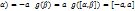

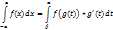
Доказательство

Пусть F(x) – первообразная f(x), тогда F’(x)=f(x) F(g(t))’=F’(g(t))*g’(t)

Пусть 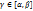и g(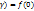

Можно заметить, что если подынтегральная функция f(x) нечетная на отрезке [a,b], то F(x) четная на этом отрезке, т.е. F(-x)=F(x)

1)рассмотрим 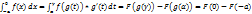=F(0)-F(a)

2) рассмотрим 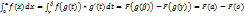=-(F(0)-F(а))

, ч.т. д

Геометрический смысл. Определенный интеграл равен площади криволинейной трапеции, ограниченной вертикальными прямыми х=а, x=b при a<b, осью Ох и графиком неотрицательной и непрерывной функции y=f(x)

9.Сходится ли интеграл ?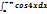

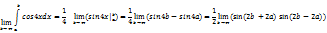
Т.к. 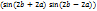ограничена, то предел существует, поэтому интеграл сходится

14. Дайте определение расстояния 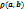между точками 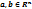. Сформулируйте и докажите свойства функции .

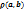В , где n>3, расстояние между точками определяется формулой

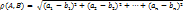
Где, А и В – две произвольные точки из .

Свойства:

1) 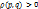, есл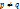и ,и ;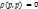

2)

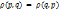
3) 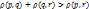- «неравенство треугольника» (1)

Доказательства: Первые два свойства очевидным образом следуют из определения расстояния.

1)Область значений функции 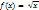равна .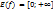

2) Дано: 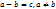, тогда 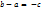; 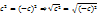. ЧТД

3) Сначала проверим неравенство (1):

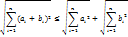
,где 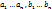– какие угодно числа. Взяв любое число х, запишем равенство 1:

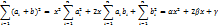
,где . Очевидно, 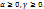Квадратный трехчлен 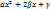, как показывает левая часть равенства 1, неотрицателен при любом значении х. Следовательно, его дискриминант 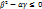, откуда имеем 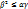, или неравенство 2:

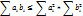
Но если возвести в квадрат обе части неравенства 1 и сократить слева и справа равные слагаемые, то получим неравенство 2.

Опираясь на неравенство 1, докажем теперь «неравенство треугольника». Если в неравенстве 1 положим, что 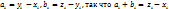, то придем к

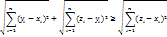
, т.е. к «неравенству треугольника» для трех точек p,q,r в .

10. Сходится ли интеграл ?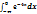

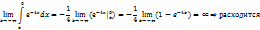
11. При каких значениях α сходится интеграл 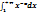? Ответ обоснуйте.

Интегральный признак сходимости. Пусть члены числового ряда 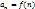являются значениями неотрицательной непрерывной функции 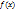, монотонно убывающей на луче [1;+∞). Тогда ряд 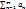и несобственный интеграл 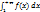сходятся или расходятся одновременно.

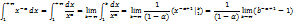
При α>1 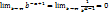, следовательно интеграл сходятся.

15. Дайте определение открытого множества в . Является ли множество 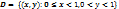открытым? Ответ обоснуйте.

Множество Х называется открытым, если все его точки внутренние. Точка р называется внутренней точкой множества Х, если она содержится в Х вместе с некоторой своей .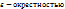

Множество 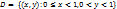не является открытым, т.к. точка 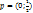, принадлежит D, но в любой её сколько угодно малой окрестности 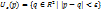есть точки, не лежащие в D (например, точки (х, у), для которых .

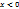16. Дайте определение замкнутого множества в . Является ли множество 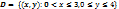замкнутым? Ответ обоснуйте.

Множество Х называется замкнутым, если оно содержит все свои граничные точки. Точка р называется граничной точкой для Х, если любая её окрестность содержит как точки, принадлежащие Х, так и точки, не принадлежащие Х. Множество 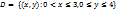не является закрытым, т.к. точка 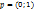, не принадлежит D, но в любой её окрестности 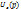есть точки, лежащие в D.

17. Дайте определение открытого множества в . Является ли множество 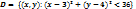открытым? Ответ обоснуйте.

Множество Х называется открытым, если все его точки внутренние. Точка р называется внутренней точкой множества Х, если она содержится в Х вместе с некоторой своей .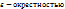

Множество 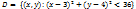является открытым, т.к. 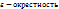точки 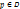лежит в D.

18. Дайте определение предельной точки множества. Приведите примеры: а) множества, содержащего все свои предельные точки, б) множества, для которого существует предельная точка, ему не принадлежащая.

Пусть Х – множество в , точка называется предельной для Х, если в любой 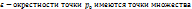Х, отличные от .

А) замкнутый круг: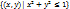

Б) замкнутый круг без своего центра 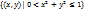. В этом случае центр (0,0) и есть та предельная точка, которая не принадлежит самому множеству.

19. Дайте определение сходящейся последовательности точек в . К какой точке в сходится последовательность 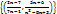? Ответ обоснуйте.

Пусть 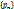- последовательность точек в . Мы говорим, что эта последовательность сходится к точке , если числовая последовательность 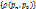имеет предел 0. Если А – предел последовательности, то говорят, что 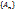сходится к точки А.

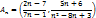
Поскольку 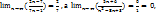то А=(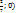

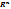20. Дайте определение сходящейся последовательности точек в . К какой точке в сходится последовательность 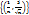? Ответобоснуйте.

Пусть 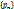- последовательность точек в . Мы говорим, что эта последовательность сходится к точке , если числовая последовательность 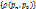имеет придел 0. Если А – предел последовательности, то говорят, что 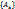сходится к точки А: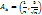

Поскольку 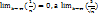= 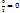, то А=(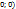

Дата добавления: 2015-03-29