Сформулируйте и докажите необходимое условие сходимости числового ряда. Приведите пример расходящегося ряда, для которого это условие выполнено

Если ряд сходится,то предел его общего члена =0.
Док-во: Пусть данный ряд сходится и его сумма равна S. Для любого натурального n имеем = + , или = - .
При n обе частичные суммы и стремятся к пределу S, поэтому из равенства следует,что
= - =S-S=0.
48. Докажите, что для сходимости ряда , 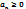необходимо и достаточно, чтобы последовательность его частичных сумм была ограничена.
Док-во: Пусть ряд 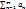сходится. Тогда существует предел его частичных сумм. Из свойств пределов следует,что посл-ть частичных сумм ограничена.
Достаточность: Т.к. все члены данного ряда положительны и для любого n Но известно, что ограниченная сверху монотонная последовательность имеет предел.
49. Сформулируйте и докажите признак Даламбера для числовых рядов с положительными членами.

Если для ряда с положительными членами

сущ. такое число q 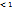, то при всех n выполняется неравенство:

то ряд сходится.Если же 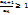для всех n, то ряд расходится.

Док-во: Отбросив несколько первых членов ряда, можно считать, что неравенство выполняется для всех n=1, 2… Перепишем это неравенство в виде .
Отсюда имеем и т.д.Вообще для любого n справедливо неравенство
.
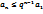Это показывает, что члены ряда не превосходят соответсвующих членов геометр прогрессии
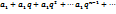Т.к. по условию 0 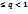, это прогрессия сходится. В силу первого признака сравнения сходится и данный ряд.
В случае,когда 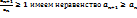, то есть члены ряда образуют неубывающую последовательность, и поэтому не выполняется необходимый признак сходимости ряда, который полностью доказывает теорему.

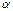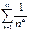52. Сформулируйте интегральный признак сходимости числового ряда с положительными членами. При каких положительных значениях ряд сходится, а при каких расходится? Интегральный признак: Пусть неотрицательная функция y=f(x) определена и монотонно убывает для x>1. Тогда для сходимости ряда f(1)+f(2)+…+f(n)+… необходимо и достаточно, чтобы сходился несобственный интеграл ∫₁^∞f(x)dx

Практика:

, при каких α ряд сходится, при каких расходится.

3) Рассмотрим случай при 0<a<1

Имеем . Сравним с , при , так как - гармонический и расходится, то по первому признаку сравнения исходный ряд тоже сходится.

4) рассмотрим случай при :

Имеем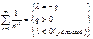

Получается: 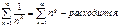, в силу того что q>0

53. Какой числовой ряд называется гармоническим? Докажите, что гармонический ряд расходится. В математике гармонический ряд представляет собой сумму, составленную из бесконечного количества членов, обратных последовательным числам натурального ряда^[1]:

.

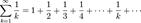Ряд назван гармоническим, так как каждый его член, начиная со второго, является гармоническим средним двух соседних. Доказать, что гармонический ряд расходится. Док-во: предположим противное. Пусть гармонический ряд сходится и существует предел S=limn→∞S_nего конечных сумм. Тогда рассмотрим предел разности его частичных сумм S_2nи S_n: limn→∞(S_2n-S_n)=limn→∞S_2n-limn→∞S_n=S-S=0. С другой стороны, разность S_2n-S_nможно оценить непосредственно: S_2n-S_n = (1+1/2+…+1/n+….+1/(n+1)+….+1/2n)-(1+1/2+…..+1/n)= 1/(n+1)+ 1/(n+2)+….+1/2n. Оценивая слагаемые, входящие в последнюю сумму 1/(n+1)> 1/2n, 1/(n+2)> 1/2n,…,1/(2n-1)>1/2n, получаем, что для любого натурального nимеет место неравенство S_2n-S_n>1/2n+1/2n+….+1/2n=n*1/2n=1/2, что противоречит условию.

54. Сформулируйте признак Лейбница для знакочередующихся числовых рядов. Приведите пример знакочередующегося ряда, сходящегося условно. Признак Лейбница.Если знаки членов ряда чередуются, а абсолютные величины, монотонно убывая, стремятся к нулю, т. е. 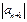< 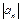и 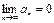, то ряд 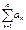сходится, а для его остатков 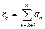выполняются неравенства: . Пусть - произвольный знакопеременный ряд. Рассмотрим ряд , составленный из абсолютных величин его членов. Если ряд 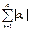сходится, то сходится и ряд 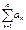, при этом ряд 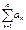называется абсолютно сходящимся. Если ряд 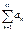сходится, а ряд расходится, то ряд 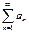называется условно сходящимся.Пример: - знакочередующийся ряд. Убедимся, что модуль общего члена монотонно убывает:

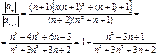>1 для всех п. Далее, 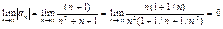. Таким образом, по признаку Лейбница данный ряд сходится. Продолжим исследование модуля общего члена данного ряда. Сравним его с общим членом гармонического ряда. Имеем . Следовательно, данный ряд, как и гармонический, расходится. Окончательно можно утверждать, что данный ряд сходится условно.

55. Сформулируйте теорему Абеля для степенных рядов. Может ли ряд 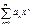, расходящийся в точке , сходиться при ? Если степенной ряд a₀+a₁x+a₂x+…+a_nx_n+… сходится при некотором х=х₀, не равном нулю, то он сходится, и притом абсолютно, при всех х, удовлетворяющих условию |х|<|x₀|; Если ряд a₀+a₁x+a₂x+…+a_nx_n+… расходится при некотором х=х₁, то он расходится при всех х, удовлетворяющих условию |х|>|x₁|

∑∞a_nxⁿ, расходящийся в точке -2 не может сходиться при х=3, т.к. |-2|<|3| следовательно согласно теореме Абеля ряд в точке х = 3 сходится, и притом абсолютно.

56. Сформулируйте теорему о почленном дифференцировании степенного ряда. Используя эту теорему, найдите сумму ряда при . Теорема о почленном дифференцировании степенного ряда: пусть функция f(x) разлагается на интервале (-R,R) в степенной ряд: f(x) = a₀+a₁x+a₂x²+…+a_nxⁿ+…(1). Рассмотрим степенной ряд: a₁+2a₂x+…+na_nx^n-1+…(2), полученный почленным дифференцированием ряда (1). Тогда:

1. ряд (2) имеет тот же радиус сходимости R, что и ряд (1).

2. на всем интервале (-R,R) функция f(x) имеет производную f^,(x), которая разлагается в степенной ряд (2).

∑nxⁿ=x∑nx^n-1=x∑(xⁿ)’=x/(1-x)²

∑xⁿ=x/(1-x) |x|<1 – сходится

∑nx^n-1=(x/1-x)’=(1-x+x)/1/(1-x)²

57. Сформулируйте достаточное условие разложимости функции в ряд Маклорена. Докажите, что функция 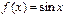разлагается в ряд Маклорена на любом интервале 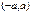. Достаточное условие разложения функции в ряд Маклорена: пусть функция f(x) определена и бесконечно дифференцируема на интервале (-R,R). Если существует такая постоянная: M=const для любого х (-R, R) <M, n=0,1,2,…, то в этом интервале ряд Маклорена сводится к функции f(x). Имеем: (sinx)’=cosx; (sinx)’’=-sinx, (sinx)’’’=-cosx, (sinx)⁽⁴⁾=sinx. Отсюда видно, что последовательность производных функции sinx периодична с периодом 4. При х=0 получаем sin0=0, sin’(0)=1, sin’’(0)=0, sin’’’(0)=-1 В общем случае все производные четного порядка равны 0, а нечетного sin^(2т+1)(0)=(-1)ⁿОтсюда ряд Маклорена для sinx:Sinx=x-(x³/3!)+(x⁵/5!)-…+(1)ⁿ(x²ⁿ⁺¹/(2n+1)!)+…

58. Сформулируйте достаточное условие разложимости функции в ряд Маклорена. Докажите, что функция 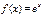разлагается в ряд Маклорена на всей числовой оси. Достаточное условие разложения функции в ряд Маклорена: пусть функция f(x) определена и бесконечно дифференцируема на интервале (-R,R). Если существует такая постоянная: M=const для любого х (-R, R) <M, n=0,1,2,…, то в этом интервале ряд Маклорена сводится к функции f(x). Пусть f(x)=e^x. В любом интервале (-r;r) имеем |f⁽ⁿ⁾(x)|= e^x<e^r. В силу признака Даламбера отсюда следует, что функция е^ч равна сумме своего ряда Маклорена при хϵ(-r;r), а значит, и для любого х ввиду произвольности r. Поскольку f⁽ⁿ⁾(0)=e⁰=1 при любом n, получаем разложение e^x=1+x+(x²/2!)+(x³/3!)+…+(xⁿ/n!)+… справедливо для всех х.

50.Сформулируйте признак Даламбера в предельной форме. Приведите пример сходящегося ряда с положительными членами, к которому этот признак неприменим.

Если существует предел: , то

1) при L < 1 ряд сходится

2) при L > 1 ряд расходится

3) при L = 1 необходимы доп. исследования. (признак неприменим)

Пример:

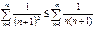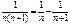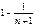Докажем сходимость: сравним с рядом: . Поскольку при всех n => достаточно доказать сходимость этого ряда. Так как , то = Т.о. 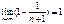. Этот ряд сходится => искомый ряд тоже сходится. Признак Даламбера не работает:

59. Сформулируйте теорему о почленном дифференцировании степенного ряда. Используя эту теорему, найдите разложение функции в ряд Маклорена, исходя из разложения функции . Теорема о почленном дифференцировании степенного ряда: пусть функция f(x) разлагается на интервале (-R,R) в степенной ряд: f(x) = a₀+a₁x+a₂x²+…+a_nxⁿ+…(1). Рассмотрим степенной ряд: a₁+2a₂x+…+na_nx^n-1+…(2), полученный почленным дифференцированием ряда (1). Тогда:

1. ряд (2) имеет тот же радиус сходимости R, что и ряд (1).

2. на всем интервале (-R,R) функция f(x) имеет производную f^,(x), которая разлагается в степенной ряд (2)

ряд для cosx получается почленным дифференцированием ряда Sinx=x-(x³/3!)+(x⁵/5!)-…+(-1)ⁿ(x²ⁿ⁺¹/(2n+1)!)+…

(Sinx)’=x’-(x³/3!)’+(x⁵/5!)’-…+((-1)ⁿ(x²ⁿ⁺¹/(2n+1)!))’+…

Cosx=1-x²/2!+x⁴/4!-…+(-1)ⁿ(x²ⁿ/(2n!)

65. Найти значение а, при котором функция 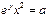является решением дифференциального уравнения 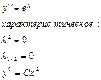- опечатка

69. Дайте определение и приведите пример дифференциального уравнения с разделяющимися переменными. Приведите уравнение к виду уравнения с разделенными переменными. Одним из наиболее простых, но весьма важных типов дифференциальных уравнений являются уравнения с разделяющимися переменными. Это дифференциальные уравнения вида: y’=f(x)g(y), где f(x) и g(y) – непрерывные функции.

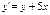
Проверим на однородность функцию:

=> однородны.

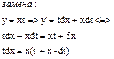
Уравнение с разделяющимися переменными.

70. Дайте определение и приведите пример автономного дифференциального уравнения. Сформулируйте свойство решений автономного уравнения. Одним из важных частных случаев дифференциальных уравнений с разделяющимися переменными являются так называемые автономные уравнения. Это уравнения вида:y’=g(y).

Замечание: Если у*- корень уравнения g(y)=0, то у=у* (у-const) является решением уравнения y’=g(y). Такое решение называется стационарным.

Теорема: Если у=фи(х) – решение автономного дифференциального уравнения, то у=фи(х+С) также является решением этого уравнения.

Пример: y’=cos(2y+2x+6). Делая замену z=2y+2x+6, находим z’=2y’+2. Следовательно, z’=2cosz+2, или z’=4cos²z/2.
71. Дайте определение уравнения Бернулли. Приведите пример.

Дифференциальное уравнение вида y’+p(x)y=f(x)yⁿ (n≠0, n≠1) называется уравнением Бернулли. Пример: y’-y=e^6x/y². Решение: n=-2. Выполним замену z=y³, получим z’=3y²y’. Далее решаем полученное уравнение: z’-3z=3e^6x

74. Установить линейную зависимость системы функций , , 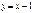. Пусть функции линейно независимы, тогда составим определитель Вронского:

W(y₁, y₂,…,y_k)=|y₁ y₂ …. Y_k|

| 2 х-1 х+1|

|y’₁y’₂ …. Y’_k| =

| 0 1 1 | = |. …………… | =0 |0 0 0 |

|y₁^(k-1)y₂^(k-1) …. Y_k^(k-1)|

значит функции лин зависимы чтд

Данные функции линейно зависимы так первую функцию можно представить в виде линейной комбинации двух других 2= 1*(x+1)+(-1)+(x-1), соответственно можно подобрать такие α1,α2,α3 при которых верно равенство: α1*y1+α2*y2+α3*y3=0

1*(x+1)+(-1)*(x-1)+(-1)*2=0

67. Сформулируйте теорему существования и единственности решения задачи Коши для дифференциального уравнения первого порядка Проверьте выполнение условий этой теоремы для задачи , Если в некоторой окрестности точки (х₀;у₀) функция f(x,y) определенная, непрерывна и имеет непрерывную частную производную f’_y, то существует такая окрестность точки (х₀;у₀), в которой задача Коши y’=f(x,y), y(x₀)=y₀имеет решение, притом единственное.

Подставим в исходное:

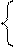
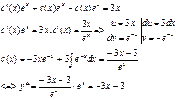
Запишем общее решение:

Подставим значения условий для задачи Коши

Ответ: с=3 и у=-3х.

68. Какое решение дифференциального уравнения называется особым? Найдите особое решение уравнения 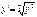. Особое решение дифференциального уравнения – это некоторая интегральная прямая уравнения, состоящая из особых точек.

Практика:

Решение уравнения, но есть особые решения при y(x)=0.

75. Докажите, что сумма частного решения линейного неоднородного дифференциального уравнения второго порядка и общего решения соответствующего однородного уравнения является общим решением линейного неоднородного уравнения второго порядка. Общее решение неоднородного уравнения L(y)=f(x)есть сумма частного решения ‾у(х) этого уравнения и общего решения соответствующего ему однородного уравнения L(y)=0. Доказательство: Покажем сначала, что сумма у(х) частного решения уравнения неоднородного уравнения ‾у(х)и произвольного решения у₀(х) однородного уравнения также является решением неоднородного уравнения. Действительно, в силу леммы имеем L(‾y+y₀)=L(‾y)+L(y₀)=f(x)+0=f(x), что и требовалось доказать. Теперь нам осталось доказать, что всякое решение у(х) неоднородного уравнения есть сумма ‾у(х) и некоторого частного решения у₀(х) уравнения L(y)=f(x). Имеем L(у-‾y)=L(y)-L(‾y)=f(x)-f(x)=0.Следовательно, у₀(х)=у(х)-‾у(х) – решение уравнения L(y)=0, значит, у(х)=у₀(х)+‾у(х), что и завершает доказательство.

Возьмем ур-е (1): . Решением ур-я(1) будет сумма частного и общего решения однородного ур-я .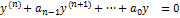

Док-во. Тогда имеем *: . Возьмем любое решение ур-я (1)**:

Вычтем их ** уравнение *, получим: ЧТД

77. Докажите, что общим решением линейного однородного дифференциального уравнения второго порядка является линейная комбинация фундаментальной системы решений этого уравнения. Пусть у₁(х),……, у_п(х) – фундаментальный набор решений уравнения L(y)=0, тогда общее решение этого уравнения задается формулой: y=C₁y₁+…+C_ny_n. Доказательство. То, что функция у(х), определяемая формулой

С₁у₁(х₀)+С₂у₂(х₀)+….+С_ку_к(х₀)=0

С₁у’₁(х₀)+С₂у’₂(х₀)+…+ С_kу’_k(х₀)=0

………………………………………………

С₁у₁^(k-1)(х₀)+С₂у₂^(k-1)(х₀)+…..+ С_kу_k^(k-1)(х₀)=-0

Является решением уравнения L(y)=0, следует из С₁у₁(х)+С₂у₂(х)+….+С_ку_к(х). Покажем теперь что любое решение ѱ (х) уравнения L(y)=0 представимо в виде линейной комбинации функций у₁,…,у_п. Зафиксируем некоторую точку х₀. Введем следующие обозначения ѱ(х₀)=у₀, ѱ’(x₀)=y’₀, …., ѱ^(n-1)(x₀)=y₀^(n-1) рассмотрим систему линейных алгебраических уравнений:

С₁у₁(х₀)+С₂у₂(х₀)+….+С_nу_n(х₀)=y₀

С₁у’₁(х₀)+С₂у’₂(х₀)+…+ С_nу’_n(х₀)=y₀

………………………………………………

С₁у₁^(n-1)(х₀)+С₂у₂^(n-1)(х₀)+…..+ С_nу_n^(n-1)(х₀)=y₀^(n-1)

Определителем этой системы является определитель Вронского для функции у₁,…у_п в точке х₀. Ввиду линейной зависимости этих функций данный определитель не равен нулю. Следовательно, у системы

С₁у₁(х₀)+С₂у₂(х₀)+….+С_nу_n(х₀)=y₀(1.1)

С₁у’₁(х₀)+С₂у’₂(х₀)+…+ С_nу’_n(х₀)=y₀

………………………………………………

С₁у₁^(n-1)(х₀)+С₂у₂^(n-1)(х₀)+…..+ С_nу_n^(n-1)(х₀)=y₀^(n-1)

Существует решение (‾С₁, ‾С₂,….,‾С_п). Тогда функция у(х)=‾С₁у₁(х)+‾С₂у₂(х)+…+‾С_пу_п(х), как это вытекает из (1.1), удовлетворяет тем же начальным условиям. В силу единственности решения задачи Коши имеем ѱ(х)=у(х), т.е. ѱ(х) есть линейная комбинация функции у₁,…у_п. теорема доказана.

78. Написать общее и частное решение с неопределёнными коэффициентами для уравнения:

y=e^λx(C₁+C₂x)

79. y=C₁e^λx+C₂е^λx; 80.у=е^ах(С₁cosβx+C₂sinβx); 82. y’’-2y’-8y=5xe^4x

Λ²-2λ-8=0; D=4+32=36; Λ_1,=-2 λ₂=4; Y=C₁e^-2x+C₂e^4x ; f(x)=P_n(x)e^ax; y=e^axx^kT_n(x), если а - корень характеристического уравнения, то К – кратность этого корня y=e^4xx(Ax+B), y=C₁e^-2x+C₂e^4x+e^4xx(Ax+B)

83. y’’-8y’+20y=e^4xsin2x; Λ²-8λ+20=0; D=64-80=-16; Λ=4+-2i

F(x)=e^ax(P_n(x)sinbx+Q_m(x)cos bx)

F(x)=e^4x(sinbx+0coxbx)

Yч=e^4xx(Asin2x+Bcos2x)

Y=e^4x(C₁cos2x+C₂sin2x)+e^4x(Asin2x+Bcos2x)

76. Докажите, что линейная комбинация решений линейного однородного дифференциального уравнения второго порядка также является решением этого уравнения. Пусть у₁(х) и у₂(х),….,у_к(х) – произвольные решения линейного однородного дифференциального уравнения и С₁, С₂,….,С_к – произвольные постоянные, тогда линейная комбинация С₁у₁(х)+С₂у₂(х)+….+С_ку_к(х) также является решением этого уравнения. Действительно, на основании L(C₁y₁+C₂y₂)= C₁L(y₁)+C₂L(y₂), имеем: L(C₁y₁+C₂y₂+….+C_ky_k)=C₁L(y₁)+C₂L(y₂)+…+C_kL(y_k)=0 что и требовалось доказать.

72. Дайте определение и приведите пример линейного дифференциального уравнения второго порядка. Докажите, что есл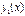и и – решения линейного неоднородного уравнения, то разность 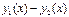является решением соответствующего линейного однородного уравнения

Линейным уравнением второго порядка называется уравнение y”+p(x)y’+q(x)y=b(x). Пример y”+5y’+6y=4sin(x).

Т.к. Y1(X) и Y2(X) явл решением, то: Y’+p(X)Y=G(X) - верное по усл

Y1’(X)+P(X)Y1(X)=G(X)-верное по усл

Y2’+P(X)Y2(X)=G(x)- верное по усл

Y1’(X)-Y2’(X)+P(X)(Y1(X)-Y2(X)))=0 –это и есть решение.

Дата добавления: 2015-03-29